| [902] Atosz | 2005-05-04 17:53:49 |
 Sziasztok!
Kissé eltűntem az utóbbi időben, de újra itt vagyok, s gondolom ilyenkor illik egy új feladattal visszatérni. Nem túl nehéz.
[161]. feladat
A távoli hegyi faluban akkor tartanak ünnepet, amikor a kolostor és a templom harangjai pontosan egyszerre konganak. Mindkét harangot szabályos időközönként, egész számú percenként kongatják; de természetesen más ritmusban. Ma a harangok déli 12-kor fognak együtt kongani. Az ünnepnapok között a harangok felváltva konganak, és előfordul, hogy a nem ünnepnapok egyikén csak egy percnyi eltérés választja el a két hangot. Legutóbb a harangszók egybeesése déli 12 órakor történt, az azóta eltelt napok száma prímszám.
Hány napja történt ez?
Jó fejtörést hozzá!
|
|
|
| [900] BohnerGéza | 2005-05-03 12:49:15 |
 Kedves Csimby!
Sajnos az asztroidra vonatkozó feltevésed nem jó. Kiszámoltam, egységnyi sugarú körben az asztroid hossza 6, a kör kerülete 2*PI.
(A számolás egy egyszerű integráláshoz vezet.)
|
| Előzmény: [884] Csimby, 2005-04-26 22:06:56 |
|
|
| [898] levi | 2005-04-29 21:47:06 |
 Nagyon érdekelne hogy hogyan lehet eljutni ahhoz a kitevőhöz (szóval tulajdonképpen a megoldás érdekelne)... persze csak ha el lehet árulni...
|
|
| [897] Csimby | 2005-04-29 19:15:31 |
 Más kérdés:
Tudja valaki, hogyan határozzák meg a felvételi ponthatárokat, milyen algoritmussal? (Ez ugyanis csöppet sem tűnik egyértelműnek)
|
|
| [896] Lóczi Lajos | 2005-04-29 17:05:01 |
 Igen, csak véletlen.
A keresett kitevő ugyanis megközelítőleg  =0.561493300750... (melyhez tartozó =0.561493300750... (melyhez tartozó 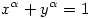 -alakzat kerülete az egységkör kerületétől csak kb. 10-12-nel tér el.) -alakzat kerülete az egységkör kerületétől csak kb. 10-12-nel tér el.)
|
| Előzmény: [895] Csimby, 2005-04-29 16:42:04 |
|
|
|
|
|
|
|
|
|
|
|
| [884] Csimby | 2005-04-26 22:06:56 |
 A kis kör sugara a nagy kör sugarának a negyede, az animációból látszik, hogy az asztroid és a nagy kör kerülete megegyezik. (egy negyed körív = egy negyed asztroid ív = a kis kör teljes kerülete)
|
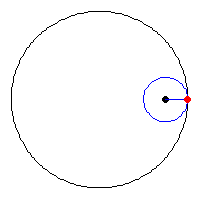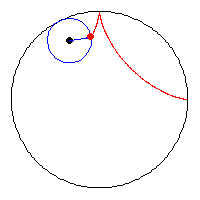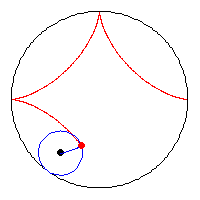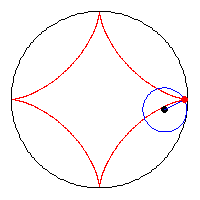 |
| Előzmény: [883] Csimby, 2005-04-26 22:02:49 |
|
|
| [882] nadorp | 2005-04-25 12:29:33 |
 Szia Csimby !
A 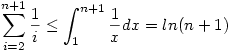 egyenlőtlenség módszerére gondoltam. Ugyanis: egyenlőtlenség módszerére gondoltam. Ugyanis:
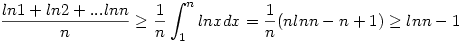 ,azaz ,azaz 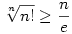 . .
A fent kapott egyenlőtlenség már jó alap a feladatban a nemkorlátosság bizonyításához.
|
| Előzmény: [881] Csimby, 2005-04-22 21:54:35 |
|
|
|
|
| [878] nadorp | 2005-04-21 11:14:46 |
 Jelentkező hiányában lelövöm a 160. feladatot.
Legyen x az a nyerőszám, amely bármely kettő nyerőszám összegének az osztója. Ekkor, ha y egy másik nyerőszám, akkor x | x+y miatt x| y is teljesül. Tehát x olyan nyerőszám, amely az összes nyerőszám osztója. Ebből következik, hogy 5x 90, azaz x 90, azaz x 18. Másrészt, mivel x ismeretében az összes többi nyerőszám egyértelműen meghatározható, ezért 6x>90 is teljesül, azaz x>15. Így x=16,17,18 jöhet csak szóba. Mivel a paritás x-et meghatározza, ezért x=17. A nyerőszámok 17,34,51,68,85. 18. Másrészt, mivel x ismeretében az összes többi nyerőszám egyértelműen meghatározható, ezért 6x>90 is teljesül, azaz x>15. Így x=16,17,18 jöhet csak szóba. Mivel a paritás x-et meghatározza, ezért x=17. A nyerőszámok 17,34,51,68,85.
|
| Előzmény: [877] lorantfy, 2005-04-18 22:42:47 |
|
| [877] lorantfy | 2005-04-18 22:42:47 |
 160. feladat: Mivel nagy nyeremény várható a lottón Mézga Aladár úgy döntött megkérdezi Köbükit, mik lesznek a nyerőszámok.
- A számokat nem mondom meg, de azt elárulhatom, hogy van köztük olyan szám amellyel bármely két nyerőszám összege osztható.
- Mi ez a szám?
- Ha megmondanám, akkor kitalálnád a nyerőszámokat.
- Legalább azt áruld el, páros vagy páratlan ez a szám.
A válasz után Aladár kitalálta a számokat, megjátszotta őket és nyert.
Mik voltak a nyerőszámok?
|
|





 <1 kitevőt (pl. ügyes programokkal), melyre a
<1 kitevőt (pl. ügyes programokkal), melyre a 

 a kerülete, és a o,1 zárt intervallumban lévő ívét vizsgáltam. Ennek az egyenlete (x-1)2+(y-1)2=1 (0
a kerülete, és a o,1 zárt intervallumban lévő ívét vizsgáltam. Ennek az egyenlete (x-1)2+(y-1)2=1 (0 x,y
x,y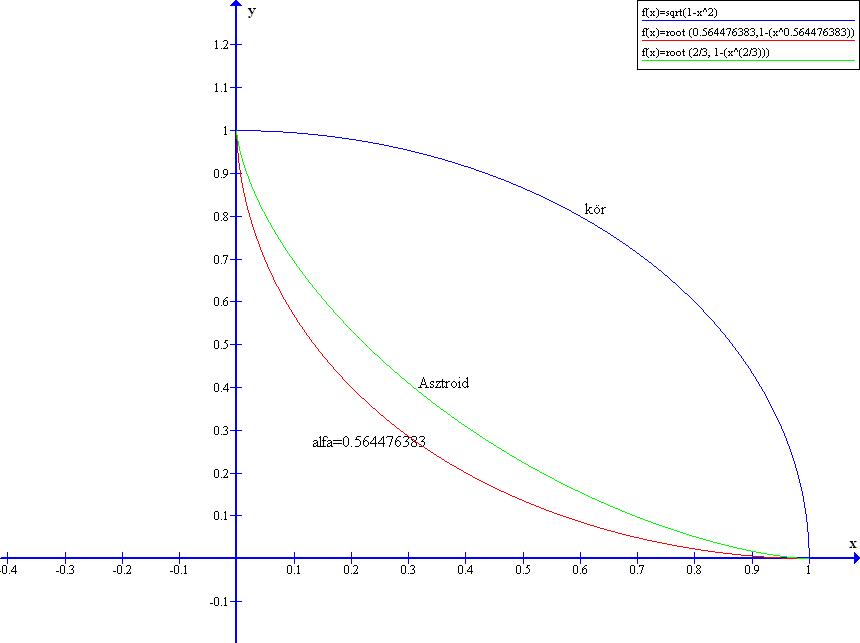

 2 értékek?
2 értékek?