|
|
| [925] Lóczi Lajos | 2005-05-09 21:58:25 |
 169. feladat. Tekintsük a 4 dimenziós térben az origó középpontú egységsugarú hipergömböt (azaz 4 dimenziós gömböt). A 4 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 4 darab egyforma, r sugarú hipergömböt. Legalább mekkora legyen az r>0 szám értéke, hogy legyen olyan pont, amely mind a 4 hipergömbön rajta van?
170. feladat. Általánosítsuk az előző kérdést n-dimenzióra, és adjuk is meg a minimális r>0 értéket a dimenzió függvényében.
|
|
| [924] Lóczi Lajos | 2005-05-09 21:55:48 |
 168. feladat. Tekintsük a közönséges 3 dimenziós térben az origó középpontú egységgömböt. A 3 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 3 darab egyforma, r sugarú gömböt. Legalább mekkora legyen az r>0 szám értéke, hogy legyen olyan pont, amely mind a 3 gömbön rajta van?
|
|
| [923] Lóczi Lajos | 2005-05-09 21:52:11 |
 167. feladat. Tekintsük a közönséges 2 dimenziós síkon az origó középpontú egységkört. A 2 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 2 darab egyforma, r sugarú kört. Legalább mekkora legyen az r>0 szám értéke, hogy e két külső körnek is legyen közös pontja?
|
|
|
|
|
|
|
| [917] Lóczi Lajos | 2005-05-05 23:16:27 |
 165. feladat. Legyen f az egész számegyenesen értelmezett, legalább kétszer deriválható korlátos valós függvény. Igaz-e, hogy f második deriváltjának van legalább egy valós zérushelye?
|
|
| [916] b.andi | 2005-05-05 22:47:36 |
 Jó én se szó szoros értelemben értettem a gúnyolódást ez inkább önirónia volt... Tudod azért teszem a röhögőfejeket a mondataim után, hogy azt nem kell halálosan komolyan venni...Amúgy tényleg köszi a segítséget!!!
|
| Előzmény: [914] jonas, 2005-05-05 20:37:50 |
|
| [915] Lóczi Lajos | 2005-05-05 22:42:01 |
 164. feladat. Számítsuk ki a
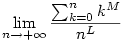
határértéket, ha M és L adott pozitív egészek.
|
|
|
| [913] b.andi | 2005-05-05 19:35:27 |
 Most kigúnyolsz? Ne máááááá..... :) mondtam hogy nem vagyok matek zseni, nekem már ez is érdekes, ha egyátalán nekifogok egy ilyen feladatnak... :) Vagy ha tudsz egy olyan topicot, hogy "Oldjatok meg gagyi feladatokat" akkor szólj :) Na mindegy amúgy nagyon nagyon köszi!!!!!! most jut eszembe nem is az volt a kérdés, hogy rajta van-e, hanem hogy mi a kör egyenlete... Nekem ez lett k:(x-3)2 + (y+4)2= 5 (vagyis négyzetgyök öt a négyzeten) (ti hogy tudtok felső indexbe írni?) és k': (x-1)2 + (y-6)2 =5 Szerintetek ez jó?
|
| Előzmény: [912] jonas, 2005-05-05 18:24:33 |
|
|
| [911] Sirpi | 2005-05-05 15:25:54 |
 Az 1. feladatot bevállalom, a többit meghagyom másoknak.
A(-2;1), B(8;1), P(0,y), ahol y az ismeretlen. Innen a PA vektor (-2; 1-y), a PB vektor (8; 1-y)
Két vektor meröleges, ha skalárszorzatuk nulla, azaz -16+(1-y)2=0, innen y=5 vagy y=-3.
|
| Előzmény: [908] b.andi, 2005-05-05 12:13:12 |
|
| [910] b.andi | 2005-05-05 15:02:07 |
 Nem adok többet ígérem!!!! :) Az előzőt rosszul csináltam mert nem a II. síknegyedbe "raktam" a pontot. Még ezenkívül a kettesbe mertem belekezdeni, végig is csináltam, de hát nem vagyok egy matek zseni... a többiről fogalmam sincs (hát a matektanárunk nem egy ász):) Egyébként ezek voltak a matek dolgozatom kérdései...
|
|
|
| [908] b.andi | 2005-05-05 12:13:12 |
 Köszi szépen!!!! Nem akarok visszélni segítőkészségeddel, de nagyon megköszönném, ha segítenél (vagy valaki más)ezekben! :)
1. Adott A(-2;1) és B(8;1). Az y tengely mely pontjaiból látszik az AB szakasz derékszög alatt?
2.Mi az egyenlete annak a körnek, melynek sugara négyzetgyök 5, és az "e": x-2y=6 egyenest A (2;4) pontjában érinti?
3. Írja fwl az (x-2)2 +(y-1)2 =5 kör y=2x egyenessel párhuzamos érintőinek egyenletét!
|
| Előzmény: [907] Fálesz Mihály, 2005-05-05 10:12:06 |
|
| [907] Fálesz Mihály | 2005-05-05 10:12:06 |
 A pont a II. síknegyedben van, a kör középpontja is ott lesz. Legyen a középpont (-a,a), a sugár a. A kör egyenlete:
(x+a)2+(y-a)2=a2.
Az egyenletnek teljesülnie kell x=-2, y=4 esetén, tehát
(-2+a)2+(4-a)2=a2
a2-12a+20=0
a=2 vagy a=10.
A két lehetséges egyenlet tehát:
(x+2)2+(y-2)2=4 és (x+10)2+(y-10)2=100.
|
| Előzmény: [906] b.andi, 2005-05-05 09:26:14 |
|
| [906] b.andi | 2005-05-05 09:26:14 |
 Hello! Megoldanátok nekem ezt a feladatot? ( csak arra vagyok kiváncsi, hogy jól dolgoztam-e): Egy kör érinti mindkét tengelyt és átmegy a P(-2;4) ponton. Mi a kör egyenlete?
|
|
| [905] Lóczi Lajos | 2005-05-04 22:34:50 |
 163. feladat. Tekintsünk egy r>0 sugarú kört egy adott perempontjához tartozó érintőegyenessel együtt. Egy teljes fordulat erejéig csúszásmentesen görgessük végig a kört az egyenesen. A kijelölt perempont eközben egy G görbét ír le. Mekkorának válasszuk r értékét, ha azt szeretnénk, hogy az egyenes és G által határolt síkidom területének és kerületének mérőszáma ugyanakkora legyen?
|
|
| [904] tudniakarok | 2005-05-04 22:18:53 |
 Na ehhez a következőt találtam:
"... július 27-ére minden adat végleges lesz ahhoz, hogy beindíthassuk a vonalhúzás számítógépes eljárását. Ez egy többszörös biztosítással lefuttatott matematikai algoritmus,mely folyamatosan összeveti az egyes intézmények és szakok irányszámait az oda jelentkezők számával és elért felvételi pontszámaival. Minden egyes szak esetében az oda jelentkezők pontszámaiból alakul ki egy sorrend,amelynek csúcsán a legtöbb pontot elért jelentkező áll, majd sorra következik a többi... a szabály az, hogy a ténylegesen felvett hallgatók száma alulról közelíti meg az irányszámot. Mindezek figyelembevételével alakul ki végül július 27-én, előreláthatólag késő este a ponthatár..."
|
| Előzmény: [897] Csimby, 2005-04-29 19:15:31 |
|
| [903] Lóczi Lajos | 2005-05-04 22:09:28 |
 Következzék egy régi feladat:
162. feladat. Tekintsünk két kört, K1-et és K2-t, sugaraik legyenek rendre 1, illetve r egység. K2 középpontja K1 peremén helyezkedik el. Mekkorának válasszuk r értékét, hogy a két körlap metszetének területe K1 területének fele legyen?
|
|




 . A kerület 8r + 2r
. A kerület 8r + 2r

