| [93] jenei.attila | 2003-11-19 13:00:17 |
 Úgy gondolom, ez a feladat nem különbözik a négyzet szerkesztésétől, ugyanis mindkét esetben adott egység mellett a négyzetgyök(2) hosszúságú szakaszt kell megszerkeszteni csak körző segítségével. Bármelyik feladat megoldása megoldja a másikat is.
|
| Előzmény: [92] Hajba Károly, 2003-11-19 00:54:04 |
|
|
| [91] Kós Géza | 2003-11-18 22:50:54 |
 A 18-szöges megoldást is nézzük meg, szerintem nagyon tanulságos.
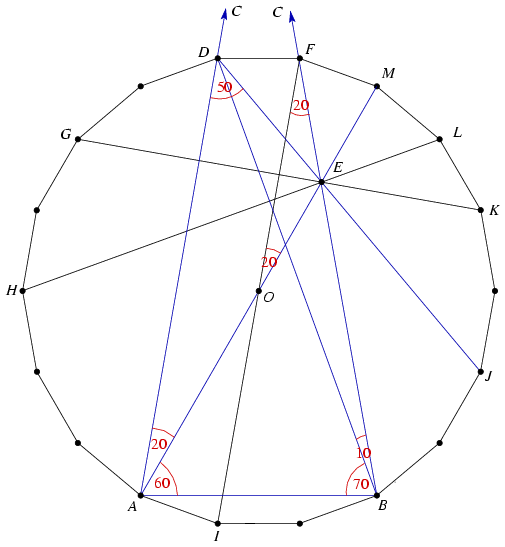
A szabályos 18-szögnek két nagy előnye van. Az egyik, hogy az átlók és oldalak közötti szögek mindig a 10o többszörösei, ezért esélyünk van megtalálni a feladat ábráját az átlók között. A másik, hogy sok olyan pont van a belsejében, ahol nagyon sok átló megy át. Az ábrán az E egy ilyen pont.
Legyen E először csak az AM átmérő és DJ metszéspontja. A DJ tükörképe az AM egyenesre KG, tehát KG is átmegy E-n. A KG egy nagyon speciális átló, a hozzá tartozó középponti szög éppen 120o. Ebből következik, hogy az O és F pontok egymás tükörképei a KG átlóra. Az OM egyenes tükörképe a KG átlóra éppen FB, mert O tükörképe F, és az irányok is stimmelnek. Tehát FB is átmegy E-n. Végül HL az FB tükörképe az AM átmérőre, tehát ez is átmegy E-n.
|
 |
| Előzmény: [63] Kós Géza, 2003-11-13 14:25:51 |
|
| [90] lorantfy | 2003-11-18 20:45:43 |
 Kedves Péter Pál!
Gratulálok! Jó a megoldás. Annyi vari lehet, hogy az első menetben egy kannibál és egy fehérember megy át és a fehérember hozza vissza a csónakot. Én már előre megcsináltam táblázatban, hogy gyakoroljam a TeX táblát:
| 3K |
3F |
|
|
|
| 2K |
2F |
F,K > |
|
|
| 2K |
2F |
< F |
K |
|
|
3F |
K,K > |
K |
|
|
3F |
< K |
2K |
|
| K |
F |
F,F > |
2K |
|
| K |
F |
< K,F |
K |
F |
| 2K |
|
F,F> |
K |
F |
| 2K |
|
< K |
|
3F |
| K |
|
K,K > |
|
3F |
| K |
|
< K |
K |
3F |
|
|
K,K > |
K |
3F |
|
|
|
3K |
3F |
|
|
| Előzmény: [89] Pach Péter Pál, 2003-11-17 21:37:15 |
|
| [89] Pach Péter Pál | 2003-11-17 21:37:15 |
 Megoldást írok a 18. feladatra:
1. lépés: Átmegy két kannibál, egyikük a túlparton marad, másikuk visszahozza a csónakot.
2. lépés: Ugyanez még egyszer.
3. lépés: Átmegy két fehérember, egyikük ott marad, másikuk viszont egy kannibál társaságában visszatér.
4. lépés: Átkel a még hátralévő két fehérember, a túlparti kannibál visszaviszi a csónakot.
5-6. lépés: Most már csak az van hátra, hogy a kannibálok is átkeljenek. Először átkelnek ketten, majd egyikük visszmegy a harmadikért.
Könnyen végiggondolhatjuk, hogy a kannibálok az átkelés során sosem kerültek többségbe. Ez azt jelenti, hogy mindannyiukat sikerült – épségben – átjuttatnunk a túlpartra.
|
| Előzmény: [79] lorantfy, 2003-11-16 17:50:10 |
|
| [88] Pach Péter Pál | 2003-11-17 21:34:00 |
 Trükkös a megoldásod, BrickTop. Egyébként nem szükséges, hogy a két ponton átmenő egyenes is adott legyen. Leírok egy megoldást, ami csak a két pont (és természetesen a körző megfelelő használatának) ismeretét feltételezi
A 20. feladat II. megoldása következik: Könnyen bizonyítható, hogy körző segítségével (vonalzó nélkül) tudunk invertálni egy pontot egy olyan körre, aminek a középpontját is ismerjük. (Ezt először külső pontra érdemes belátni.) Aki nem ismeri, gondolkozzon el rajta.
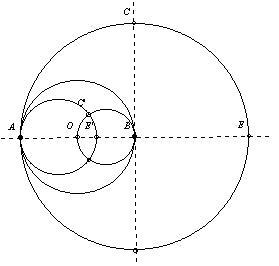
A két pont, amihez négyzetet akarunk rajzolni, legyen A és B!(A keresett négyzet ABCD.) AB-hez háromszögrácsot rajzolva megkapjuk A tükörképét B-re: E-t. Most E-t invertáljuk az A középpontú, AB sugarú körre, a képe az AB szakasz felezőpontja, O lesz. Az O középpontú, 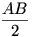 sugarú kör legyen k. C-t megkaphatjuk a B középpontú, AB sugarú kör, és a B-ben AB egyenesére állított merőleges egyenes (egyik) metszéspontjként. Ha ezt a két alakzatot invertáljuk k-ra, akkor az egyenesből is kör lesz, és így már meg tudjuk szerkeszteni metszéspontjukat. A körünk képe az AE’ átmérőjű kör, ahol E’ az E pont képe, ugyanis O illeszkedik AE-re. (Ezt a kört meg tudjuk rajzolni, hiszen felezőpontját megszerkeszthetjük ugyanúgy, ahogy AB felezőpontját megszerkesztettük. Az egyenesünk képe a BO átmérőjű kör. sugarú kör legyen k. C-t megkaphatjuk a B középpontú, AB sugarú kör, és a B-ben AB egyenesére állított merőleges egyenes (egyik) metszéspontjként. Ha ezt a két alakzatot invertáljuk k-ra, akkor az egyenesből is kör lesz, és így már meg tudjuk szerkeszteni metszéspontjukat. A körünk képe az AE’ átmérőjű kör, ahol E’ az E pont képe, ugyanis O illeszkedik AE-re. (Ezt a kört meg tudjuk rajzolni, hiszen felezőpontját megszerkeszthetjük ugyanúgy, ahogy AB felezőpontját megszerkesztettük. Az egyenesünk képe a BO átmérőjű kör.
A két kapott kör metszéspontjai közül az egyik C’, vagyis C képe. Ha C’-t invertáljuk k-ra, akkor megkapjuk a keresett C pontot. Természetesen D ugyanígy kapható meg.
A 20. feladat speciális esete a Mohr-Mascheroni-tételnek, ami a következő állítást bizonyítja: „Minden körzővel és vonalzóval elvégezhető szerkesztés elvégezhető csak körző segítségével is.” Erről, és még számos híres matematikai problémáról olvashatunk Heinrich Dörrie: A diadalmas matematika c. könyvében. (Szóval ez most egyben könyvajánlás is!) A könyvet egyébként az egyik matektanárunk, Hraskó András ajánlotta.
|
 |
| Előzmény: [87] BrickTop, 2003-11-17 20:48:41 |
|
| [87] BrickTop | 2003-11-17 20:48:41 |
 20. feladat, megoldás: Adott A és B pont.
1) A-ból és B-ből körívezünk AB-vel --> C metszéspont.
2) A-ból és C-ből körívezünk AB-vel --> D metszéspont.
3) A-ból és D-ből körívezünk AB-vel --> E metszéspont.
4) E-ből körívezünk BD-vel --> F metszéspont az AB szakaszon.
5) B-ből körívezünk BE-vel, D-ből körívezünk FB-vel --> G a két körív metszéspontja (a két körív valójában érinti egymást).
6) F-ből körívezünk EG-vel --> a keletkezett körív és a B középpontú, AB sugarú körív (ld. 1)) metszéspontja a négyzet harmadik pontja, H.
7) H-ből körívezünk AB-vel :) --> a keletkezett körív és az A középpontú, AB sugarú körív (ld. 1)) metszéspontja a négyzet negyedik pontja.
Kicsit több, mint egy éve jöttem rá erre a megoldásra. Most megprobáltam szerkesztéssel ellenőrizni, nem nagyon jött ki, de biztos azért, mert bénán szerkesztek. Elméletileg szerintem jó. Bizonyítást nem írtam, mert ha megvan az ábra, már nagyon egyszerű belátni, hogy a négyzet pontjait kapjuk. Ábrát nem készítettem, mert lusta voltam (órákig tartana egy ilyen ábrát megcsinálni az én programarzenálommal), és mert az ábra lelövi a poént. Így aki meg akarja oldani a feladatot, egyszerűen nem olvassa el a szerkesztés menetét.
Remélem nem néztem el semmit és nem vesztegettem el negyed órát egy hibás szerkesztés leírásával :)
|
| Előzmény: [86] SchZol, 2003-11-17 20:07:20 |
|
|
| [85] BrickTop | 2003-11-17 18:32:42 |
 A 20. feladatban a 2 pont nincs véletlenül összekötve? Mert nekem van megoldásom, de csak ha egy szakasz van megadva (tehát 2 pont ami össze van kötve).
|
| Előzmény: [84] SchZol, 2003-11-17 17:14:16 |
|
| [84] SchZol | 2003-11-17 17:14:16 |
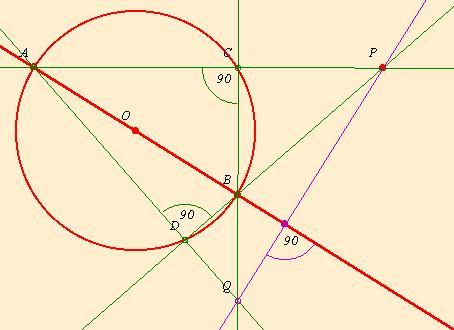
 PQ azért merőleges AB-re, mert PAQ háromszögben QC és PD magasságvonal, tehát B a PAQ háromszög magasságpontja, ebből következik, hogy AB egyenes is magassága a PAQ háromszögnek, tehát merőleges AB PQ-ra.
20.feladat: Adott két pont. Egyetlen körző segítségével rajzoljunk négyzetet, melynek e két pont két szomszédos csúcsa.
|
| Előzmény: [83] lorantfy, 2003-11-17 16:41:14 |
|
| [83] lorantfy | 2003-11-17 16:41:14 |
 Mivel csak vonalzót használhatunk mást nem is tehetünk csak összekötünk két pontot. PA majd PB. Ezek metszik a kört C és D pontokban. Ezután CB, AD ezek metszik egymást Q-ban.
Bizonyítandó: PQ egyenes merőleges AB-re!
|
 |
| Előzmény: [82] jenei.attila, 2003-11-17 15:32:04 |
|
| [82] jenei.attila | 2003-11-17 15:32:04 |
 Kedves László!
Köszönöm a szép ábrát, kicsit reméltem is, hogy lesz türelmed megrajzolni. Maradva a geometriánál, egy nem túl nehéz de érdekes feladat: adva van egy kör, a középpontján átmenő egyenes, és egy pont a körön és egyenesen kívül. Egy egyenes vonalzó használatával szerkesszünk a ponton átmenő, egyenesre merőleges egyenest.
|
| Előzmény: [81] lorantfy, 2003-11-17 15:15:00 |
|
|
| [80] jenei.attila | 2003-11-17 13:18:39 |
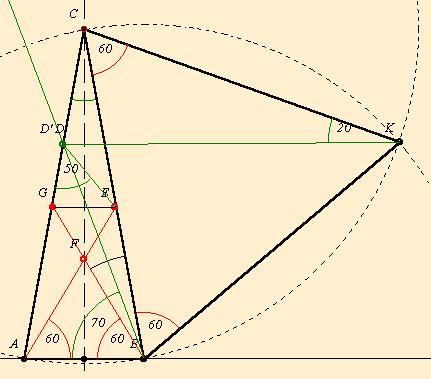
 Utoljára az általam feladott háromszöges feladatról. Csillag megoldása ABD szög=50 fok esetére ismét nagyon ötletes és egyszerű. Én jóval körülményesebben oldottam meg, mégis leírom, mert megoldja az ABD=70 fok esetet is. Tehát: Szerkesszünk a BC oldalra kifelé szabályos háromszöget, amelynek harmadik csúcsa legyen K. A D´ pontot AC-n vegyük fel úgy, hogy CKD´ szög=20 fok legyen. Megmutatjuk, hogy ekkor D és D´ egybeesik. Valóban, mivel D´CK szög=80 fok és CKD´=20 fok, ezért CD´K=80 fok és KC=KD´=KB. A D´KB szög=40 fok, ezért (és KD´=KB miatt) KBD´ szög=70 fok. De KBD szög is =70 fok, ezért D´=D. Megállapítottuk tehát, hogy a CDK háromszög egybevágó az ABC háromszöggel, ezért CD=AB. De GD=GC-CD=GB-CD=GB-AB=GB-FB=GF, és GF=GE miatt GD=GE, amiből GDE=50 fok, és EDB=20 fok.
Az ABD=50 fok esete: D helyett L-lel jelöljük a szóbanforgó pontot, és D maradjon meg az előzőek szerint, tehét ABL szög =50 fok és EDA szög=50 fok. Szintén DC=AB=AL miatt AEL és CED háromszögek egybevágók, ezért EL=ED, de LDE szög =50 fok (D-t most így vettük vel, nem az előző feladatból jött, bár egybeesik vele), DLE szög is = 50 fok, amiből ELB szög =80 fok.
Bocs a hosszú hozzászólásért, legközelebb rövidebb leszek.
|
|
| [79] lorantfy | 2003-11-16 17:50:10 |
 Kedves Fórumosok!
Biztos ismeritek azt a feladatot, hogy vigyük át a farkast a nyulat és a káposztát a folyón, ha a csónakunkban csak egy hely van és a farkas megeszi a nyulat, a nyúl meg a káposztát ha egyedül hagyjuk őket. Ha nem, olvassátok el a Szegény ember káposztája c. Gárdonyi mesét:
http://www.brody.iif.hu/hmek/gardonyi/tihanyi/kaposzta.htm
Ennek egy variációja a következő: 18. feladat:
A folyó egyik partján áll 3 kannibál és 3 fehérember. Egy kétszemélyes csónakjuk van és úgy kell átkelniük a folyón, hogy egyik parton sem lehetnek többségben a kannibálok, mert akkor megeszik a fehérembereket. A csónakban ülő partotérő emberek már partonlévőnek számítanak.
|
 |
|
| [78] Csillag | 2003-11-14 22:27:12 |
 Üdv Mindenkinek!
Azt hiszem jobb lenne, ha ettől a témakörtől elválasztanánk a "divatosabb" témákat: pl. Rubik-kocka, billiárdgolyók,...
Más: a (66)-os hozzászólásomban: nem paralelogramma, hanem deltoid a DFEG négyszög:)
GB
|
|
| [77] toto | 2003-11-14 18:38:51 |
 http://www.superliminal.com/cube/cube.htm
Itt lehet találni egy virtuális, négydimenziós 3x3x3x3-as kockát. Nem volt időm megnézni, de lehet olyan érdekes, mint egy 4x4x4 es
|
| Előzmény: [71] SchZol, 2003-11-14 05:48:40 |
|
| [76] Bubu | 2003-11-14 17:32:18 |
 Üdvözletem! Csatlakoznék a kockás cikk kérőihez. Másrészt elmélkedtem a saját problémámon (a 2 hibás golyó esete), az mindenesetre biztosnak tűnik, hogy teljes általánosságban nem megoldható. Úgyhogy a feladat része lett az is, hogy találjuk ki a feladatot:) Egyébként nagyon tetszik a fórum, kár hogy egyelőre kevesen vagyunk. Remélem hamar híre megy, és akkor akár komolyabb problémák is szóba jöhetnek - mint anno a levélváltások...:))
Bubu
|
|
| [75] Hajba Károly | 2003-11-14 13:12:31 |
 Kedves László!
A geodéták, mikor a tervezési alaptérképhez a térképet digitalizálják a meglévő kézzel, tustollal rajzolt állapotról, egyszerűen csak azt mondják: 'bedigizem neked a térképet'. Nem azt mondom, hogy szép, de mindenképpen rövid és már egyes helyeken használják.
Károly
|
| Előzmény: [73] lorantfy, 2003-11-14 12:56:58 |
|
| [74] Hajba Károly | 2003-11-14 13:01:02 |
 Visszatérek a biliárdgolyós feladathoz, mivel úgy tűnik számomra, még sok érdekes dolgot lehet kihozni belőle.
- [39] hozzászólásbeli Gáti Baetrix Zoltán által közzétett táblázata a nehezebb változatnak éppen nem felel meg, de ha a 3. mérésben a 8-as golyót a 12-esre cseréljük, már tökéletes.
- [52]-beli Bubu hozzászólásában a több eltérő golyó felé általánosít. Bennem pedig már korábban felmerült egy másik általánosítási lehetőség, miszerint valamely golyó(k)ról állítjuk, hogy nem tér el és ez alapján, hogy változik a mérhető golyók száma. Továbbá mi a helyzet a kevesebb ill. több mérési számok esetén.
16. feladat: Ha n a mérések száma, mennyi a legnagyobb g(n) golyók száma, mely esetén még meghatározható a hibás golyó és annak eltérése is?
17. feladat: Ha 2-szer mérhetünk, hány biztosan nem hibás golyót kell ismernünk, hogy a lehető legtöbb ismeretlen golyó közül tudjuk kiválasztani az egyetlen hibás golyót és eltérését?
Hajba Károly
|
|
| [73] lorantfy | 2003-11-14 12:56:58 |
 Kedves Károly, Zoli és Kockarajongók!
Feltúrtam a fizika szertárt és megtaláltam a Fizikai Szemle 82/2-es számában a cikket. Jövő héten beszkennelem és recognitázom - szóval nyomtatott formából elektronikus formába alakítom. (Jó lenne erre egy egyszerű szó - a digitalizálni talán nem a legszerencsésebb - ha tudtok jobbat írjátok meg!) Az érdeklődőknek tudom küldeni.
|
| Előzmény: [72] Hajba Károly, 2003-11-14 08:40:05 |
|
| [72] Hajba Károly | 2003-11-14 08:40:05 |
 Kedves Zoli!
Isten hozott a kockabűvöltek táborába!
Beszkennelem a cikket, de feltételezem, hogy a Fizikai Szemlebeli cikk részletesebb lehet. Ti. késöbb jelent meg és többen jegyezték.
> Ti láttatok már 4*4*4 Rubik-kockát?
Anno volt a kezemben egy, talán kölcsön is kaptam egy hétre, de lehet, hogy az a dodekaéder volt. Ki tudja, ezirányú emlékeimet belepte már a rozsda. Tény, hogy nem bírtam vele :o(
Üdv: Károly
|
| Előzmény: [71] SchZol, 2003-11-14 05:48:40 |
|
| [71] SchZol | 2003-11-14 05:48:40 |
 Kedves Károly!
Engem érdekelne a Rubik-kockás cikk, ha beszkenneled. Nagyon szeretem a Rubik-kockát, hetente egy párszor mindig kirakom. Ti láttatok már 4*4*4 Rubik-kockát? Sajnos Én még nem láttam, csak hallottam róla.
Üdv, Zoli
|
|
| [70] Hajba Károly | 2003-11-13 23:50:18 |
 Kedves László!
Nem azt a cikket ismerem, hanem a könyvbelit (A bűvös kocka - Gondolat - 1981), amit még csak Marx jegyzett (no nem a Tőkés :o).
A 'spin' pedig, hát... anno szerettem a fizika ezen részét is.
Ha érdekel a könyvbeli cikk, megpróbálhatom beszkennelni és drótpostán elküldeni.
Üdv: Hajba Károly
|
| Előzmény: [68] lorantfy, 2003-11-13 23:16:47 |
|
| [69] lorantfy | 2003-11-13 23:22:51 |
 Az 5. feladatra: még nem írtunk megoldást. Az eredeti szöveg: Adott 100 láda mindegyikben 1000 db 2 grammos 1 forintos, kivéve egyet amiben 1 grammosak az 1 forintosok. Legkevesebb hány mérésből tudjuk eldönteni melyik ládában vannak a selejtes egy forintosok, ha minden láda ugyanúgy néz ki, és csak egy egykarú mérlegünk van.
Aki nem ismeri annak érdemes átgondolni a trükköt: Sorszámozzuk meg a ládákat 1-100-ig és minden ládából tegyünk fel a mérlegre annyi forintost amennyi a láda sorszáma. Ezt mérjük le. Ha minden ládában 2 grammos érmék lennének akkor (1+100)x100 = 10100 grammot kellene mérnünk. Amennyivel kevesebbet mérünk annyi a keresett láda sorszáma.Tehát egy mérés elegendő.
Az eredeti kitűző – Sch Zoli – nehezítése:
15. feladat: Hány mérés szükséges, ha a 100 közül két ládában vannak 1 grammos forintok.
|
| Előzmény: [6] SchZol, 2003-11-01 22:12:06 |
|