| [952] jonas | 2005-06-05 20:39:58 |
 Megpróbálom.
Tegyük fel, hogy az f folytonos függvény az egész R-en értelmezett, és minden értéket pontosan kétszer vesz fel.
Vegye fel az y0 számot az x0 és x1 pontokban, ahol x0<x1. Tekintsük az (x0,x1) intervallumot! Mivel itt f nem veszi fel x0-t, vagy csak y0-nál nagyobb, vagy csak y0-nál kisebb értéket vesz fel. Szimmetriaokokból tegyük fel, hogy csupa nagyobbat vesz fel. Ezen a középső intervallumon a függvénynek van maximuma, mégpedig az x2 pontban, ahol f(x2)=y2.
Legyen y3 a másik pont, ahol f(y3)=x2. A szimmetria miatt feltehetjük, hogy y2<y3
Két eset lehetséges.
Vagy x2<x3<x1, de ekkor az (y2,y3) intervallumban f értéke kisebb y2-nél, de nagyobb y0-nál. De az ilyen értékeket f a közbülsőérték-tétel miatt az (y0,y2) és az (y3,y1) intervallumon is mind felveszi, tehát legalább három helyen is, ami ellentmondás.
Ha viszont x1<x3, akkor f az (y0,y2), (y2,y1) és az (y1,y3) intervallumon is felveszi az összes (x2,x3)-beli értéket, ami lehetetlen.
|
| Előzmény: [951] Lóczi Lajos, 2005-06-05 19:29:33 |
|
|
|
| [949] Lóczi Lajos | 2005-06-04 15:56:10 |
 Igen, igazad van, a [946]-ban kétszer is tévedtem: persze "-" helyett ott "+"-t akartam írni, másrészt rosszul láttam, hogy "nem igaz" -- szerintem is jó a képlet, amit írtál.
|
| Előzmény: [948] 2501, 2005-06-03 19:49:31 |
|
| [948] 2501 | 2005-06-03 19:49:31 |
 Megpróbálom indokolni, hogy
![f_n(x) \quad = \quad \left[\frac x n\right]+x-[x]](keplet.cgi?k=DA10EEB0EC3F69C7)
(ahol ![\left[x\right]](keplet.cgi?k=DAA57752EF9A484F) az alsó egészrész) szerintem miért működik. Bontsuk fel két függvény összegére: az alsó egészrész) szerintem miért működik. Bontsuk fel két függvény összegére:
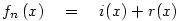
![i\left(x\right) \quad = \quad \left[\frac x n\right]](keplet.cgi?k=A7FADA218258A5C7)
![r\left(x\right) \quad = \quad x-\left[x\right]](keplet.cgi?k=3C012AAE469F98BB)
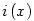 grafikonja egy n hosszúságú "fokokból" álló, növekedő "lépcső", melyben a "fokok" az egészeknél kezdődnek. grafikonja egy n hosszúságú "fokokból" álló, növekedő "lépcső", melyben a "fokok" az egészeknél kezdődnek. 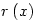 tulajdonképpen x törtrésze (írhattam volna tulajdonképpen x törtrésze (írhattam volna 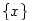 -et is), tehát a grafikonja negyvenöt fokos, és 1 magas "sörtékből" áll. A kettő összegének grafikonján a "sörték" rákerülnek a "lépcsőfokokra", és minden fokon éppen n darab lesz. -et is), tehát a grafikonja negyvenöt fokos, és 1 magas "sörtékből" áll. A kettő összegének grafikonján a "sörték" rákerülnek a "lépcsőfokokra", és minden fokon éppen n darab lesz.
|
| Előzmény: [944] 2501, 2005-06-02 21:51:06 |
|
|
| [946] Lóczi Lajos | 2005-06-03 16:48:28 |
 175. feladat. Adjunk meg olyan folytonos valós függvényt, amelynek értelmezési tartománya az egész számegyenes és minden értéket pontosan kétszer vesz fel.
|
|
| [945] Lóczi Lajos | 2005-06-03 16:45:44 |
 (A kérdőjeles egyenlőség nem igaz.)
Másrészt nem is működnek jól a képletek, pl. a bal oldali esetén (ha [.] jelöli az alsó egészrészt (=floor)), akkor pl. ![x-[x]-[\frac{x}{2}]](keplet.cgi?k=5F969C09B1B31D18) a felet 3-szor veszi fel, de az egész értékeket csak kétszer. a felet 3-szor veszi fel, de az egész értékeket csak kétszer.
|
| Előzmény: [944] 2501, 2005-06-02 21:51:06 |
|
| [944] 2501 | 2005-06-02 21:51:06 |
 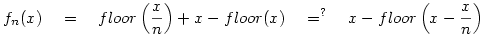
Aggodalomra semmi ok, mára befejeztem.
|
|
| [943] 2501 | 2005-06-02 20:57:45 |
 Megint nem jó, csak f2(x) jó. :o(
|
|
| [942] 2501 | 2005-06-02 20:43:40 |
 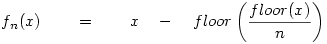
Ahol floor(x) az a legnagyobb egész szám, amely nem nagyobb x-nél. Így biztosan jó.
|
|
| [941] 2501 | 2005-06-02 19:38:23 |
 Mégsem jó, pl. f2(x) három helyen 0. :o)
|
|
| [940] 2501 | 2005-06-02 19:07:11 |
 174.
fn(x) = x - [x] mod n
Ez leírja az egész függvénycsaládot. Legalábbis most jónak tűnik. :o)
|
|
| [939] Lóczi Lajos | 2005-06-01 13:40:51 |
 174. feladat. Adjunk meg olyan valós függvényt (ha van), amelynek értelmezési tartománya is és értékkészlete is az egész R, és minden értéket pontosan
a.) kétszer
b.) háromszor
c.) négyszer
vesz fel.
|
|
| [938] Lóczi Lajos | 2005-05-18 21:12:23 |
 173. feladat. Adjuk meg az összes olyan pozitív x,y,z számot, melyekre teljesül, hogy
xy=yz=zx.
(A feladat más, mint a régebbi hasonló kinézetű társa.)
|
|
| [937] Lóczi Lajos | 2005-05-18 15:56:07 |
 A "nem létezik" helyett persze jobb "nem létezik véges"-et mondani. (Én talán annyival gondoltam egyszerűbbre, hogy f(x)=1 és 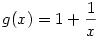 is megfelelnek ellenpéldaként a 171. feladatban.) is megfelelnek ellenpéldaként a 171. feladatban.)
Ennyi előkészítés után végre következhet a tényleges feladat.
172. feladat. Legyenek f és g olyan, az egész számegyenesen értelmezett, deriválható függvények, hogy 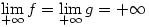 és és 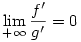 . .
Igaz-e, hogy ekkor 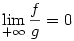 ? ?
|
| Előzmény: [936] nadorp, 2005-05-18 07:50:32 |
|
| [936] nadorp | 2005-05-18 07:50:32 |
 Úgy látszik, az analízis nem túl népszerű. Az alábbi megoldás biztos nem a legegyszerűbb, de általános.
A válasz nem, ugyanis legyen p(x)az egész számegyenesen deriválható függvény, és tegyük fel, hogy 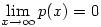 ( ilyen pld. e-x). ( ilyen pld. e-x).
Legyen f(x)=ep(x)-p(x) és g(x)=p(x). Ekkor:
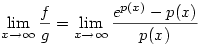 nyilván nem létezik, viszont nyilván nem létezik, viszont
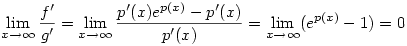
|
| Előzmény: [934] Lóczi Lajos, 2005-05-10 16:57:48 |
|
|
| [934] Lóczi Lajos | 2005-05-10 16:57:48 |
 Rendben, gondoltam, hogy ezzel semmi gond nem lesz. Akárcsak ezzel:
171. feladat. Tegyük fel, hogy 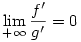 . Igaz-e, hogy ekkor . Igaz-e, hogy ekkor 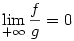 ? ?
(Ezután már csak egy variánsom lesz, ami az igazi feladat.)
|
| Előzmény: [931] nadorp, 2005-05-10 11:05:27 |
|
| [933] levi | 2005-05-10 13:52:19 |
 nem tud vki vmi olyan könyvet/bármit ami a 4,5,...dimenziós geometriával foglalkozik? elkezdett érdekelni a dolog, gondoltam itt biztos tud vki vmi ilyet ajánlani...
|
|
|
|
| [930] neo | 2005-05-10 01:07:15 |
 Http://matek2005.fw.hu
|
|
| [929] Lóczi Lajos | 2005-05-10 00:23:57 |
 Gratulálok, nekem is ezek az értékek jöttek ki (bár én sehol sem használtam geometriai meggondolásokat -- vannak példák arra, hogy az analógiáink magas dimenzióban nem működnek), úgyhogy azért a többieknek is maradhat még annyi a feladatból, hogy vagy igazoljuk a geometriai érvelésedet, vagy geometriától függetlenül oldjuk meg a problémát.
|
| Előzmény: [928] levi, 2005-05-09 23:50:42 |
|
| [928] levi | 2005-05-09 23:50:42 |
 167-170. feladatra: a két dimenziós eset vizsgálata: vegyük a két külső kör középpontját, ezek A(r+1,0) és B(0,r+1). Vegyük azt a szakaszt amit ez a két pont határoz meg, a keresett legkisebb sugarú kör érinti egymást, mégpedig a szakasz felezőpontjában, így már adott ennek is a koordinátája, a sugár egyenlő a felezőpont és az egyik külső kör középpontjának távolságával, r-re rendezés után szerintem ez: 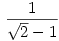 . .
Három dimenziós esetben kössük ismét össze ezeket a pontokat, ezek egy háromszöget fognak meghatározni. a keresett pont a háromszög magasságpontja. a háromszög szerencsére szabályos, így a magasságpont egybeesik a súlyponttal, a súlypont koordinátái pedig kiszámíthatóak a csúcsok koordinátáiból... ismét felírva egy középpont és a magasságpont távolságát az egyenlő lesz r-rel , és utána rendezve megkapjuk r-t, ami nálam 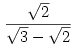
ezután az általános n dimenziós eset: sajnos nem tudok 4 vagy magasabb dimenzóban látni, és annak a (koordináta)geometriáját sem tudom, de talán az előző két esetből levont következtetésem jó lesz... szóval a körök középpontjai adottak, a keresett pont mely egyenlő távolságra van mindegyiktől szerintem K(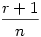 , , 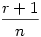 ,..., ,...,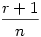 ) (összesen n-szer). Ekkor egy középpont és a K távolsága lesz egyenlő a sugárral. Mivel a középpontok mind egy-egy tengelyen vannak, ezért koordinátái közül pontosan egy lesz r+1 az összes többi 0. Ha felírjuk a távolságképletet, majd kiemelünk a gyök alól ) (összesen n-szer). Ekkor egy középpont és a K távolsága lesz egyenlő a sugárral. Mivel a középpontok mind egy-egy tengelyen vannak, ezért koordinátái közül pontosan egy lesz r+1 az összes többi 0. Ha felírjuk a távolságképletet, majd kiemelünk a gyök alól 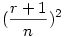 -t, akkor azt kapjuk hogy -t, akkor azt kapjuk hogy 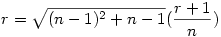 . Rendezzük r-re, majd egyszerűsítünk, akkor azt kapjuk hogy . Rendezzük r-re, majd egyszerűsítünk, akkor azt kapjuk hogy 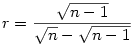 . Ezalapján az n=4 eset már könnyen kiszámolható... . Ezalapján az n=4 eset már könnyen kiszámolható...
|
|






