|
| [978] lorytibi | 2005-07-20 17:37:37 |
 Hát igen, ha egy ilyet hall az ember, ami teljesen lehetetlennek tűnik, rögtön tudja, hogy meg lehet csinálni! Segítségemre volt a tesóm, aki egy gyönyörű animációt csinált erre nekem. Ebből nagyon szépen látszik, hogy meg lehet csinálni ... Sajnos azt nem tudom feltenni, csak egy képet belőle. Lényeg, hogy a a kockát a testátlónál furjuk át, és így pont átfér egy ugyanakkora kocka (Az ábrán a kékes kockát furtam át, és a zöldet dugom át rajta)
|
 |
|
|
| [976] Atosz | 2005-07-20 12:09:48 |
 Közben eszembe jutott egy újabb érdekes feladat!
Át lehet-e fúrni egy tömör fakockát úgy, hogy egy másik ugyanolyan méretűt egyben átdugjunk a lyukon?
|
|
| [975] Atosz | 2005-07-20 11:53:55 |
 Kedves Viktor!
Ez a megoldásod jó, de így tényleg fejben kell tartani kilenc kártyalapot, ami nem könnyű! A hármas számrendszer könnyebb, az megy csukott szemmel is csak azt kell hallani, hogy hová kerül a jelzett csomag. Minden jót!
|
| Előzmény: [973] xviktor, 2005-07-20 09:19:32 |
|
| [974] Atosz | 2005-07-20 11:50:12 |
 Szia Onogur, és mindenki!
Tökéletes a megoldásod, gratulálok! Pontosítva úgy működik, hogy ha a kiválasztott csomag felülre kerül akkor 0, ha középre, akkor 1, ha alulra akkor pedig 2 lesz a megjegyzett érték. Ezt megcsinálva háromszor egymás után, akkor kapunk egy hármas számrendszerbeli számot, amit visszafelé olvasva konvertálunk át (azaz az első összerakás kódja adja az egyes helyiértéket, míg az utolsóé a kilencest) tizesbe, ami adja a kártya helyét. Elég hatásos!
Más! Tartozom még nektek Onogur régebbi karikás feladatának általánosításával, azaz hogyan lehet tetszőleges sok karikát összefűzni úgy, hogy egyben marad (csak vágással jönne szét) ám bármelyiket felvágva minden karika leszedhető lesz. (Lásd a fotón!) Ha esetleg nem látszana jól, akkor nagyjából leírva: Az elsőn átbújtatjuk a másodikat, két végét lehajtjuk, majd azon a két fülön a harmadikat, annak is lehajtjuk a végeit, stb... majd az n-iket egy normál karikával lezárjuk.
ui: (Onogurnak) Könyv!
|
 |
| Előzmény: [971] Hajba Károly, 2005-07-20 08:29:41 |
|
| [973] xviktor | 2005-07-20 09:19:32 |
 Lenne egy megoldasom, ami egyedul a "csukott szemnek" mond ellent, de kivancsi lennek a velemenyekre:
A 27 kartya 3 pakliba kerul. Egyikre ramutatunk igy mar csak 9 kartya lehet jo. A kovetkezo osztasnal a 9 kartya 3as csoportokban kulon kerul /3-3-3/, igy a masodik ramutatas utan mar csak 3 kartya lehet a jo. Az utolso osztasnal a maradek 3 kartya is kulon-kulon kerul, igy a vegen mar konkretan tudni fogjuk melyik a valasztott kartya.
Egyben lenne egy masik feladatom. Attila feladatat nem olvastam el rendesen, es azt hittem Gergonne rakja tetszolegesen egymasra a paklikat. Ha igy lett volna, hogyan tudta volna mindenfele szamolgatas nelkul megmondani melyik lap a keresett /ezt mar lehet csukott szemmel is csinalni/.
Udv: Viktor
|
| Előzmény: [972] xviktor, 2005-07-20 08:38:45 |
|
|
| [971] Hajba Károly | 2005-07-20 08:29:41 |
 A trükk matematikai alapja a következő lehet:
32-5=27=33
Minden kirakásnál megfigyeli hogy az a hármas hova kerül és ebből lehet kiszámolni. Egy hármas számrendszerbeli szám jön ki, amit fejben átkonvertál 10-esre és megvan a kártya helye. A részleteket még ki kell dolgozni, de ez az alapelv.
O.
|
| Előzmény: [965] Atosz, 2005-07-19 19:44:48 |
|
| [970] Atosz | 2005-07-20 07:54:08 |
 Sziasztok!
Mindenkivel megosztom Viktornak írt gondolataimat, nehogy mások is tévútra menjenek. Természetesen matekfeladatról van szó, amit Gergonne gondolt ki, de nem túl nehéz, ám érdekes. A bűvész tulajdonképpen csukott szemmel is dolgozhat, nem kell látnia, hogy melyik lap hova kerül és a néző (a lap gondolója) szedi össze mindhárom esetben a kiskupacokat, tehát a jelzett kiskupac bárhová kerülhet, azaz felülre, középre, alulra. Minden jót!
|
|
| [969] xviktor | 2005-07-19 22:50:14 |
 Ujabb otletem tamadt. Azt is elkuldtem e-mailben.
|
|
|
|
|
| [965] Atosz | 2005-07-19 19:44:48 |
 Sziasztok!
J.D.Gergonne francia matematikus kártyatrükkje volt a következő feladvány:
A 32-lapos kártyacsomagból (pl. magyarkártya) kiveszünk 4 hetest és egy nyolcast, majd a néző a maradékokból rágondol egy lapra. Ezután a jól megkevert csomagot szinével felfelé balról jobbra, egyesével három kupacba kirakjuk (bal, közép, jobb, bal, közép, jobb, stb...). A néző megmutatja nekünk, hogy melyik kupacban van a gondolt lap, majd tetszőleges sorrendben egymásra helyezi a kupacokat. A paklit megfordítjuk (így a szine lesz lefelé), majd egyesével újra kezdjük a kirakást (természetesen megint minden lerakott lapot szinével felfelé teszünk az asztalra, hogy lássa őket). Ezt az egész kirakás, megmutattatás, összeszedés dolgot összesen háromszor megcsináljuk, majd az egész paklit sorba kiterítjük és megmutatjuk a gondolt kártyát.
Kérdés, hogy mi a trükk? (Természetesen matematikai feladványról van szó!)
Minden jót, Atosz!
|
|
| [962] 2501 | 2005-06-14 11:12:21 |
 Nem csak az N, Z, Q, R, stb. számhalmazok, hanem ezek részhalmazai is (pl. a páros számok halmaza).
Ezt felhasználva egy lehetséges megoldás:
a 3-mal osztva
A: 0 vagy 1
B: 1 vagy 2
C: 2 vagy 0
maradékot adó számok halmazai.
|
| Előzmény: [961] Kérdező, 2005-06-14 10:19:25 |
|
| [961] Kérdező | 2005-06-14 10:19:25 |
 A példám egyszerű, de mégsem ugrik be a megoldás. Kérlek segítsetek!
----Halmazelmélet----
Adott 3 számhalmaz, melyekben külön-külön végtelen sok elem van. Egy-egy halmaz metszetében szintén végtelen sok elem található. Viszont a közös metszetben nulla, az ugyanis üres!
Hogy lehetséges ez? Tudomásom szerint ugyanis a számhalmazok egymás elemei...
R > Q > Z > N
Tehát két ilyen számhalmaz metszetét mindig a kisebbik halmaz elemei jelentik. Nem értem, hogy a közös metszet hogy lehet üres!?
Előre is köszi a segítséget!
|
|
| [960] jonas | 2005-06-13 21:51:02 |
 A g(x)=x+1 is jó ellenpélda mindhárom esetre. A g(x)=1-et én is kipróbáltam, de úgy látszik, nem vettem észre, hogy az is mindig jó. Szerintem ez bizonyítja, hogy én nem számoltam túl sokat, hiszen csak beírtam az első olyan ellenpéldát, ami kijött.
|
| Előzmény: [959] Lóczi Lajos, 2005-06-13 14:45:33 |
|
| [959] Lóczi Lajos | 2005-06-13 14:45:33 |
 Hogy hogy tudtok ilyen bonyolult ellenpéldákat kifundálni :-), g(x)=x+1, egy csomót kell számolni, hogy leellenőrizze az ember.
(Ami nekem -- igaz, sajnos nem öt perc után -- beugrott, mint ellenpélda, az a szimpla g(x):=c választás: ez alkalmas c-vel mindegyiket cáfolja. Szinte érzem, hogy sugallják a feladat kitűzői, hogy próbáljuk meg a cx alakú függvényeket, mint "jobb szélső" esetet, 0 és 1 közötti c-vel, ezekre azonban mindhárom eset teljesül...)
|
| Előzmény: [958] jonas, 2005-06-12 18:54:39 |
|
| [958] jonas | 2005-06-12 18:54:39 |
 Nem baj, ha lelövöm a megoldást?
Ha g(x)=1, akkor 0= g'(x) így a feltétel teljesül, de g'(x) így a feltétel teljesül, de 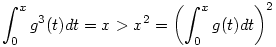 ha 0<x<1, tehát (a) vagy (c) biztosan nem mindig igaz. ha 0<x<1, tehát (a) vagy (c) biztosan nem mindig igaz.
Másrészt a (b) sem feltétlenül igaz, szerintem g(x)=x+1 ellenpélda rá.
|
| Előzmény: [957] Lóczi Lajos, 2005-06-12 14:09:43 |
|
| [957] Lóczi Lajos | 2005-06-12 14:09:43 |
 177. feladat. Nemrég valahol tesztkérdésként (!) tűztek ki egy, az alábbihoz hasonló feladatot (tehát úgy gondolom, nem volt túl sok idő a megoldására).
Válasszuk meg a g:(0, ) ) R deriválható függvényt tetszőlegesen úgy, hogy 0 R deriválható függvényt tetszőlegesen úgy, hogy 0 g'(x) g'(x) 1 teljesüljön minden x>0 esetén. Döntsük el, melyik állítás igaz mindig. 1 teljesüljön minden x>0 esetén. Döntsük el, melyik állítás igaz mindig.
a.) Minden x (0,1) (0,1)
b.) Minden x 1 1
c.) Minden x>0
esetén fennáll, hogy
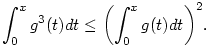
|
|
| [956] Lóczi Lajos | 2005-06-12 13:45:31 |
 Szép megoldás. Beírom, hogy a feladatra milyen "megoldást" láttam, tanulságos a kettőt összehasonlítani. (Idézőjelbe tettem azokat a részeket, ami miatt a két megoldás látszólagosan elétér.)
Alkalmazzuk a jobb oldalon a tangensfüggvény ismert "azonosságát",
és a rövidség kedvéért pl. legyen y:=tg(x), valamint a:=tg(1) ekkor azt kapjuk, hogy
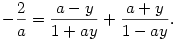
Ez utóbbi egyenletnek azonban y-ban nincs megoldása, "tehát" a kiindulási egyenletnek sincs.
|
| Előzmény: [955] levi, 2005-06-10 20:15:33 |
|
| [955] levi | 2005-06-10 20:15:33 |
 -2ctg1=tg(1-x)+tg(1+x)
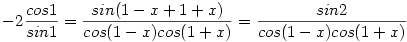
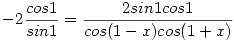
-cos(1-x)cos(1+x)=sin21
-(cos1cosx+sin1sinx)(cos1cosx-sin1sinx)=sin21
sin21sin2x-cos21cos2x=sin21
sin21sin2x-(1-sin21)(1-sin2x)=sin21
sin21sin2x-(1-sin2x-sin21+sin21sin2x)=sin21
-1+sin2x=0
sin2x=1
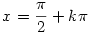
+ellenörzés (remélem nem baj hogy azt nem írom ide)...
|
| Előzmény: [954] Lóczi Lajos, 2005-06-09 14:30:46 |
|
| [954] Lóczi Lajos | 2005-06-09 14:30:46 |
 176. feladat. Oldjuk meg a valós számok halmazán az alábbi egyenletet:
-2ctg1=tg(1-x)+tg(1+x)
|
|
|











 g'(x) így a feltétel teljesül, de
g'(x) így a feltétel teljesül, de  )
) R deriválható függvényt tetszőlegesen úgy, hogy 0
R deriválható függvényt tetszőlegesen úgy, hogy 0 (0,1)
(0,1)  1
1