| [1003] xviktor | 2005-08-08 18:23:15 |
 Az egesz levezetese sztem:
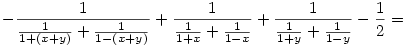
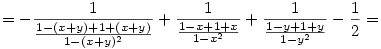
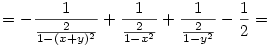
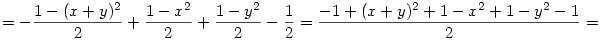
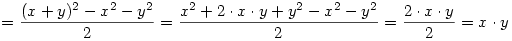
Amennyiben elirtam valamit legyszives szoljatok.
Udv: Viktor
u.i.: megtalaltam a szorzas jelet :)
|
|
|
| [1002] xviktor | 2005-08-08 17:12:05 |
 Az x2 fuggvenyt a kovetkezokepp lehet megcsinalni szerintem:
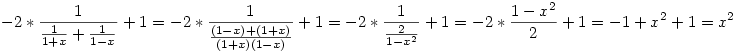 . .
Miutan megvan x2 Jonas modszerevel megvan x*y fuggveny is.
Udv: Viktor
u.i.: Legyszives segitsetek, hogy szorzas jelet hogy lehet beirni TeXben? Elore is koszi.
|
| Előzmény: [1001] rizsesz, 2005-08-08 16:28:41 |
|
| [1001] rizsesz | 2005-08-08 16:28:41 |
 Tyű, köszönöm :) a négyzet viszont számomra elérhetetlennek tűnik a páratlan kitevők miatt :( Engem is az gátolt meg eddig, és közeledek. :) segítsééééég!
|
|
| [1000] jonas | 2005-08-08 15:35:15 |
 Ezt a feladatot már hallottam, de nem tudom a teljes megoldást.
A segítség az volt hozzá, hogy állítsuk elő a négyzetre emelést először. Ha az már megvan, akkor 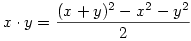 ; ahol kettővel osztani tudunk, mert ; ahol kettővel osztani tudunk, mert 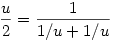
Most azt kéne megpróbálni, hogyan lehet x2-et előállítani. Eddig nem tudom, hogyan lehet, de még gondolkodom rajta.
Valami olyasmit kell használni, hogy 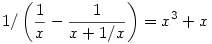 ... ...
|
| Előzmény: [989] rizsesz, 2005-08-06 21:42:56 |
|
|
| [998] rizsesz | 2005-08-07 16:46:03 |
 (elnézést, zárójelezgetni is lehet). tehát mondjuk előállítható az 1/(x+y) kifejezés, x-2y, stb, míg azonban n*m esetén nem jó az m+m+m+m...+m (n-szer) (n és m valós szám). tehát összegezve valami olyasmi a feladat, hogy lehetséges-e két számot összeszorozni csak a +, - és 1/x műveletek segíségével úgy, hogy bármely két szám esetén mindig ugyanazokat a műveleteket hajtjuk végre (mintha egy képletbe helyettesítenénk be) függetlenül a két számtól.
|
|
| [997] Yegreg | 2005-08-07 16:07:05 |
 Tehát egy olyan polinomra gondolsz, ahol x és y csak 1 és -1 hatványon lehet, és az együttható is csak 1 vagy -1 lehet mindenhol? Valamint a tagok száma véges, és nem változóval kifejezhető?
Érdekes feladat így.
Üdv
Yegreg
|
|
|
|
|
|
|
|
| [990] Yegreg | 2005-08-06 22:41:45 |
 Kedves Péter!
Kössz a címet, de én jobban megértem a saját gondolatmenetem alapján. Az már kiderült számomra, hogy az n dimenziós általánosítás helyes, mert megkérdeztem valakitől, és az mondta, hogy összegezni kell váltott előjellel a különböző dimenziós felületek számát -1-től n-ig(n dimenzióban), és 0 kapunk.(negatívval kezdjük)., Valamint, hogy a -1 dimenziós felületek száma mindig 1, és az n dimenziósé is.
És ha megnézzük, akkor ez pontosan ugyanaz, mint az enyém, egy kis átalakítás után.
Szóval, örülök, hogy rájöttem, és szeretném bizonyítani az én gondolatmenetem, legfeljebb majd utána elolvasok más gondolatmeneteket és bizonyításokat is.
Bár a nem egyszereű poliéderekre vonatkozó általánosítás helyességéről még nem kaptam visszajelzést(igaz, azt a részt magam is bizonyítottam, csak ide nem írtam le), de eddig minden egyes esetben helyes eredményt adott, bár megjegyezték, hogy néha talán nehezen használható. Valójában nem annyira, szerintem, de ez további gondolkodásra késztetett.
ScarMan barátom említette, hogy ismer egy c+l=e+2-2*k képletet, k lyukú tórusszal ekvivalens alakzatokra, ami nyilván adott esetben könnyebben használható, mint az enyém, ezekután gondoltam arra, hogy talán a speciális tulajdonságokat(ami jelen esetben a tórusz-ekvivalencia) beírva a képletbe, megkaphatjuk a speciális formulát.
Az ötlet helyesnek bizonyult, a tóruszoknál legalábbis biztosan. Ha a legvégsőként beírt képletet nézitek... Az egyszerű poliéderek száma, melyekre felbontjuk a tóruszt k. Jelen esetben k=1(ez most nem a lyukak száma, csak a képletben volt így), méghozzá egy véges henger, ha úgy tetszik gömb, amire a "standard" Euler tétel vonatkozik. A tóruszt minden lyukánál található gyűrűben "elvágjuk", így nyilván gömbbel ekvivalens alakzatot kapunk, az egyszerű poliéder pedig önmagával érintkezett akárhány csúcson és ugyanannyi élen, ezek a képletben kiejtik egymást, valamint minden egyes lyuk körüli gyűrűben pontosan két lapon(a vágás mentén, ha úgy tetszik), és mivel k(visszatérva ScarMan képletéhez, bocs, hogy a k-t két dologra használtam) lyukú tóruszról volt szó, így egy 2*k a bal oldalon, ezt ha átvisszük a jobb oldalra, akkor látható, hogy a barátom által említett c+l=e+2-2*k képletet kapjuk, tehát az általam felírt képlet alkalmas speciális esetekre vonatkozó egyenletek levezetésére.
Tulajdonképpen, feltehetőleg ekvivalens a Péter által írt címen található képlettel, csak ahhoz jobban meg kellene nézni.
Igazából azért írtam le a képletet, mert a gondolatmenetem bizonyítására vártam ötleteket, nem azért, hogy leírjátok az általános Euler tételt, mert ez már az. Csak esetleg más alakban, mint ismeritek.
Ha bizonyításként az választjátok, hogy leírjátok a ti képletetek levezetését, és belátjátok, hogy az ekvivalens az enyémmel, az elfogadható, bár mint már mondtam, nekem most nem ez lenne a célom, pontosan ezért nem néztem meg könyvben sem, mert hajlamos lennék én is így letudni, ahelyett, hogy a saját gondolatmenetemet bizonyítanám.
Üdv
Yegreg
|
|
| [989] rizsesz | 2005-08-06 21:42:56 |
 Sziasztok, egy elég meglepő probléma ütött szöget a fejembe: elő kellene állítani az f(x;y)=x*y függvényt az összeadás, kivonás és reciprok műveletek segítségével, de természetesen nem jó az x szerepeljen y alkalommal :) szóval valahogy elő kellene állítani x*y-t :)
|
|
| [988] Maga Péter | 2005-08-06 17:43:29 |
 Kedves Yegreg!
Az n-dimenziós Euler-formulát megtalálod a következő helyen minden érdekességgel: www.cs.elte.hu/~mg, ez Moussong Gábor tanár úr (ELTE, geometria tanszék) honlapja. Ezen a helyen a Konvex halmazok és politópok affin térben című, pdf kiterjesztésű állomány vége, a 6.10-6.12 pontok tartalmazzák ezt. A bizonyításhoz sajnos kell némi előismeret, főként lineáris algebra.
Minden jót!
Maga Péter
|
| Előzmény: [984] Yegreg, 2005-07-31 18:30:01 |
|
| [987] Yegreg | 2005-08-01 00:58:20 |
 Na jó, most kérek elnézést, hogy iszonyat sok hozzászólásom volt egymás után, de az eredeti képletet, amit írtam, már végiggondoltam, a nem egyszerű polinomos kiegészítést pedig általában írás közben találtam ki, és ezért több hibám is volt benne, most leírom az utolsó javított verziót, ha pedig észreveszem, hogy rosszul írtam ismét, akkor végiggondolom rendesen. Szóval itt lenne(két előjelet rontottam):
![\sum_{i=0}^{[\frac{(n-1)}2 ]}{\big(b_{2i}+b_{kozos_{2i}}\big)}-\sum_{j=0}^{[ \frac{n}2 ]-1}{\big(b_{2j+1}+b_{kozos_{2j+1}}\big)}=2*(n-2[\frac{n}2])*k](keplet.cgi?k=D82050B71C2D455C)
Bocsánat mégegyszer...
Yegreg
|
|
| [986] Yegreg | 2005-08-01 00:45:01 |
 Nah, sikerült!
Így nézne ki
![\sum_{i=0}^{[\frac{(n-1)}2 ]}{\big(b_{2i}-b_{kozos_{2i}}\big)}-\sum_{j=0}^{[ \frac{n}2 ]-1}{\big(b_{2j+1}-b_{kozos_{2j+1}}\big)}=2*(n-2[\frac{n}2])*k](keplet.cgi?k=5D108C04ECE8A701)
Az egészen általános képlet, ahol k már nem az izolált részek száma, hanem a poliédert alkotó egyszerű poliéderek száma, bkozosx pedig a poliéderen(vagy poliéderben) található olyan összes x-brán száma, amely nem csak egy egyszerű polinomhoz tartozik. (azért kozos, mert a közös-t nem szerette a TeX...).
Szóval így nézne ki egészen általánosan...
Na, a feladat még mindig a régi...
Üdv:
Yegreg
|
|
| [985] Yegreg | 2005-08-01 00:31:51 |
 Na jó, a k-t felejtsétek el(illetve ne felejtsétek, csak ne úgy jegyezzétek meg, ahogy írtam, mert az úgy nem jó), mert ha csak úgy hajítom bele a k-t, akkor nem törődnék azzal, hogy lesznek közös lapok(pontosabban n-1-bránok), vagyis kiesnek páran. Tulajdonképpen most jut eszembe, hogy nem is kell elfelejtenetek a k-t, csak jobb oldalt ki kell egészíteni, méghozzá egy ilyesmivel:
...-k*bkn-1átl.
És ezúttal megjegyezném, hogy ScarMan ismét tévedett, de azért kössz, hogy szólt azzal kapcsolatban, hogy én is tévedtem.
Jah és némi magyarázat a jobb oldal kiegészítéséhez: ki kellett vonni a közös n-1 bránok számát. Nah, és ezután most jut eszembe, hogy nem csak ilyen nem egyszerű polinom lehet. ŐŐŐŐ....kérnék lyan 5 percet, és utána beírom a rendes általános képletet nem egyszerű polinomokkal is, vagy akit az nem érdekel, az maradjon a
![\sum_{i=0}^{[\frac{(n-1)}2 ]}{b_{2i}}- \sum_{j=0}^{[ \frac{n}2 ]-1}{b_{2j+1}}=2*(n-2[\frac{n}2])](keplet.cgi?k=3EFD1E39D4438431)
képletnél egyszerű polinomok esetén. Nemsokára újra jelentkezem. Üdv:
Yegreg
|
|
| [984] Yegreg | 2005-07-31 18:30:01 |
 Pár napja írt egy e-mailt egy barátom(az fórumon ScarMan néven), írta, hogy emlékszem-e még, amikor az Euler tétel n-dimenziós általánosításáról beszéltünk, valamint elküldte az egyik ötletét. Aztután a másnap délelőttöt azzal töltöttem, hogy gondolkoztam, majd arra jutottam, hogy helytelen az egyenlete, és kitaláltam egy egyenletet, ami feltehetőleg helyes. Íme: ![\sum_{i=0}^{[\frac{(n-1)}2 ]}{b_{2i}}-
\sum_{j=0}^{[ \frac{n}2 ]-1}{b_{2j+1}}=2*(n-2[\frac{n}2])*k](keplet.cgi?k=B06847CB32B1ED8E)
Ahol n a dimenziók száma, bx az n dimenziós test x-bránjainak(x dimenziós felületeinek, azaz x=0-nál csúcs, x=1-nél él, x=2-nél lap, x=3-nál test stb.) száma, k pedig az izolált és összefüggő részek száma(ez csak akkor szükséges, ha nem egyszerű a polinom). A képletet az alapján kaptam meg, hogy kiindultam abból, hogy egy n-1 dimenziós testre igaznak kell lennie az n dimenziós Euler tételnek, ha figyelembe vesszük azt, hogy az n-1 dimenziós testnek pontosan 2 db n-1-bránja van, de ez logikus, hiszen két oldala van. A képletet úgy kapjuk meg, ha feltételezzük, hogy ez az állítás megfordítva is igaz.
Az ok, ami miatt többek között beírom ezt ide az, hogy a képlet megkapása utáni 2-3 napban nem sikerült bizonyítanom, hogy a fenti állítás megfordítottja igaz, a feladat tehát az lenne, hogy igazoljuk a képlet helyességét, vagy cáfoljuk meg azt.
Sok sikert!
Üdv:
Yegreg
|
|
| [983] Yegreg | 2005-07-30 19:14:02 |
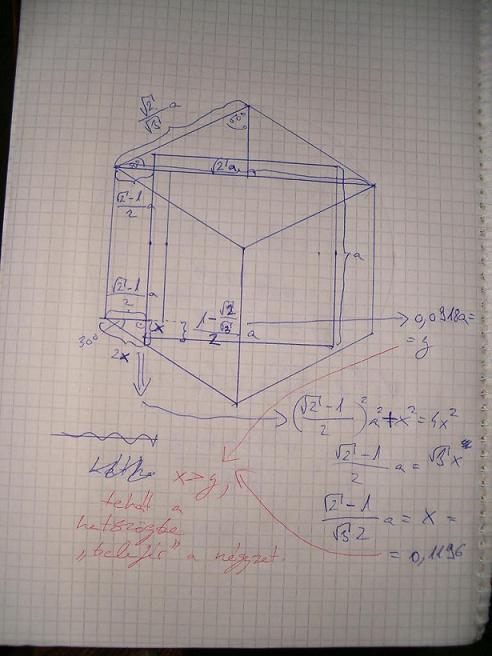
 A kockás feladat megoldása: Legyen a kocka éle a! ha úgy forgatjuk a kockát, hogy egy szabályos hatszöget lássunk(azért forgatjuk így, mert a testátlóval párhuzamosan akarjuk keresztükfúrni), akkor a hatszög oldalai nyilván nem a hosszúságúak lesznek, mondjuk a perspektívikus torzulás miatt, de hívhatjuk máshogy is. Meg kell tehát kapnunk a hatszög oldalait, ehhez kell egy ismert érték, ami pedig egy olyan szakasz, ami egy olyan nézetből, ahol valahány oldal valóban a, a forgatás egyenesével párhuzamos. Ilyen lehet egy olyan nézet, ahol csak a kocka egyik oldalát, azaz egy négyzetet látunk, ilyenkor a négyzet oldalai nyilván a hosszúságúak. A négyzet nézetből két felső csúcsa(azaz a lapátló) körül megfelelően forgatva a hatszögnézetet kapjuk, és mivel a lapátló körül forgattunk, annak hossza változatlan, azaz gyök 2*a. Innentől a számításokat az ábrán láthatjátok (sajnos nincs olyan kafa programom, mint LoryTibinek, de van kafa füzetem és kafán tudok béna ábrákat csinálni, de remélem azért látható minden). A számítások végén megkapjuk, hogy a hatszögbe írható az a oldalú négyzet, azaz így kifúrva átfér rajta a másik kocka. Az, hogy a kifúrt test egybefüggő még be kell látni, pl. ha egy gráfként ábrázoljuk az új testet, akkor látjuk, hogy az eredeti kocka két csúcsát és hat élének egyrészét hagytuk el, valamint az is láthatjuk, hogy a kocka megmaradt hat csúcsának és a fúrás során létrejött másik hat csúcsok bármelyikét köti őssze él másik csúccsal és nincsen izolált rész, valamint a számolásokból kiderül, hogy a fúrás után is az élekhez pozitív térfogat tartozik, azaz tulajdonképpen nem tűnt el él, csak részük. Azért az is igaz, hogy ténylég éppen, hogy befér, hiszen egy 1m*1m*1m-es kockánál csak 1,39 cm-en "múlik".
Üdv:
Yegreg
|
 |
|
| [982] lorantfy | 2005-07-28 11:30:00 |
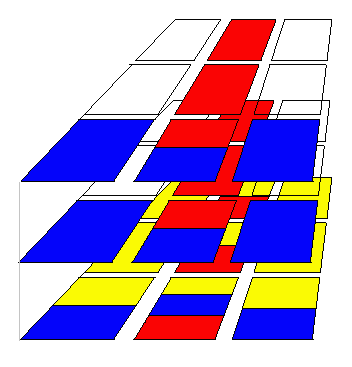
 Atosz 178. feladata ennek a 3 D-s változata. A 3 egymásutáni kirakás és választás után azt tudjuk meg, hogy a gondolt lap pl. a sárga szinten, a piros oszlopban és a kék sorban van. A 3 információ egyértelműen megadja a gondolt lapot és persze ezekből a gondolt lap szorszáma is kiszámolható az utolsó összegyűjtéskor kapott pakliban.
A kirakás módja garantálja, hogy először pl. az azonos szinteken lévő kártyák vannak azonos kupacban, majd az azonos oszlopokban, majd az azonos sorokban lévő 9-9-9 lap kerül azonos kupacba.
|
 |
| Előzmény: [981] lorantfy, 2005-07-28 11:14:20 |
|
| [981] lorantfy | 2005-07-28 11:14:20 |
 Kedves Atosz, Károly, Viktor és Érdeklődők!
Nagyon jó az Atosz által [966]-ban feladott kártyás feladat. Legyen a 178. feladat.
Gyerekkoromban mi is csináltuk ennek a 2 dimes változatát. 9 db kártyát kiraktunk 3x3-as alakzatba és Béla gondolt egy lapra megmondta melyik oszlopban van.
Most összeszedjük a kártyákat oszloponként, lesz 3 kupac, ezeket egymásra helyezzük. Megfordítjuk a csomagot és újra kirakjuk soronként. Béla most is megmondja melyik oszlopban van a kártya és már tudjuk is melyik lapra gondolt Béla.
Na most, ha az elején, miután kiraktuk a 3x3-as alakzatot, azt kérjük Bélától: Gondoljon egy kártyára és mondja meg melyik sorban és melyik oszlopban van és ezután mi kitaláljuk melyik a gondolt lap, Béla köröhög minket!
Pedig valójában pontosan ez történik. Igaz Bélának mindkétszer oszlopszámot kell mondania, de a kártyák beszedése és újra kirakása miatt, gyakorlatilag ugyanaz történik.
Az ábrán a szemléltetés kedvéért direkt kiválogattam a kártyákat. Tfh. Béla a piros királyt választja. Tehát először a 2. oszlopot mondja - ebből tudjuk, hogy királyról van szó. Az összeszedés és újra kirakás után a 3. oszlopot mondja - ebből tudjuk, hogy piros szinű kártyáról van szó.
A lényeg az, hogy bár mindkétszer oszlopszámot mondott Béla, az újrakirakás miatt ez két független koordináta és ebből egyértelműen megadható a gondolt lap.
|
 |
| Előzmény: [980] xviktor, 2005-07-21 14:40:39 |
|
|










