|
| [2186] Willy | 2007-08-01 02:36:51 |
 Szia Cckek!
Nem vagyok valami penge a diffegyenltekből, de megnéztem egy próbafüggvényre:
Legyen
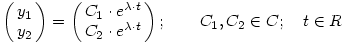
(Érzésem szerint ez a próbafüggvény minden megoldást vissza fog adni.)
Végezzük el a mátrixszorzást és a próbafüggvény deriválását is:
![\left(\matrix{y_1\cr y_2\cr}\right)'= \left( \matrix{C_1\cdot \lambda \cdot e^{\lambda\cdot t}\cr C_2\cdot \lambda \cdot e^{\lambda\cdot t}\cr} \right)= \left[\matrix{1&2\cr -1&3\cr}\right]\cdot \left( \matrix{C_1\cdot e^{\lambda\cdot t}\cr C_2\cdot e^{\lambda\cdot t}\cr} \right)= \left(\matrix{(C_1+2C_2)\cdot e^{\lambda\cdot t}\cr (-C_1+3C_2)\cdot e^{\lambda\cdot t}\cr}\right)](keplet.cgi?k=1B896813E872F5CC)
Ebből kapunk egy három paraméterrel rendelkező, egyváltozós, két egyenletből álló egyenletrendszert:
C1. =C1+2C2 =C1+2C2
C2. =-C1+3C2 =-C1+3C2
Elsőből kifejezzük C2-t, beírva a másodikba és rendezve, kapjuk:
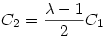
0=C1.( 2-4. 2-4. +5) +5)
1) Ezek alapján C1=C2=0 és   R azaz R azaz 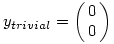
2) Avagy,  1,2=2 1,2=2 i, C1 i, C1 R és R és 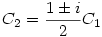 , azaz , azaz
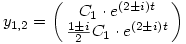
A három megoldás...
|
| Előzmény: [2183] Cckek, 2007-07-29 20:18:25 |
|
|
|
| [2183] Cckek | 2007-07-29 20:18:25 |
 Adott az 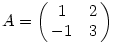 . Oldjuk meg az y'=Ay differenciálegyenletet. . Oldjuk meg az y'=Ay differenciálegyenletet.
|
|
|
| [2181] epsilon | 2007-07-29 14:01:01 |
 Helló Cckek, a Te szimpatikus feladatodra akartam választ adni, de egy sorral lennebb klickeltem, így a Doom nickre hívatkozik a válasz!
|
|
| [2180] epsilon | 2007-07-29 13:58:09 |
 Helló! Ha jól számoltam akkor a tört abszolútértéke 1/3, nem de? Pl. végezzük el a z=3+z' transzformációt, így a feltétel alapján abs(z')=1 ezért jelölje z"=konjugált(z). Így 1/z'=z" továbbá ha az abs[(4-z)/(4+z)]=E akkor E=abs[(3z'+1)/(3z'+9)]=1/3*A ahol A=abs[(3z'+1)/(z'+3)]. Most a tört számlálóját és nevezőjét is tagonkénz osztva z'-tel, a konjugálás tulajdonsága alapján azt kapjuk, hogy A=1/A adódik, és A>0 tehát A=1, így E=1/3.
|
| Előzmény: [2177] Doom, 2007-07-28 19:57:48 |
|
| [2179] epsilon | 2007-07-29 13:10:22 |
 Kösz Doom! Az még vettem észre, azzal valóban jobban be lehet osztani csoportokra, de valójában azt a keresési módszereket hiányolom, amikor konkrét szóra, stb. lehetne rákeresni, de gondolom, hogy ezt nem könnyű megvalósítani, mert már megtették volna, nem Én találnám fel a spanyolviaszt! Üdv: epsilon
|
| Előzmény: [2176] epsilon, 2007-07-28 19:35:48 |
|
|
| [2177] Doom | 2007-07-28 19:57:48 |
 A hozzászólások felett jobb felül: hány hsz legyen a lapon és rendezze a legöregebbel kezdve... innen már te is ki tudod egyszerűen számolni, hogy melyik sorszám hányas lapra esik... ;)
Ha olyan gyorsabb keresésre gondoltál, ami kulcsszavak alapján működne, az szerintem is hasznos lenne.
|
| Előzmény: [2176] epsilon, 2007-07-28 19:35:48 |
|
| [2176] epsilon | 2007-07-28 19:35:48 |
 Kedves Károly! Hát így sorszámszerint valahogy könnyebb volt betájolni, de tényleg kár, ha nem létezik olyan keresés, hogy ha beírod az adott hsz számát, akkor oda vigyen...de hát meglehet, hogy csak Nekem hiányzik. Mindenképpen kösz a segítséget! Üdv: epsilon
|
|
| [2175] epsilon | 2007-07-28 19:27:14 |
 Kedves Károly! Kösz, de nem találok valami szapora keresési lehetőséget, mint pl. a Neten, itt látom a [1. oldal] [2.oldal][3. oldal][4. oldal]...lehetőségeket, de a hozzászólások hosszából hogyan lehet megsaccolni, hogy melyikbe esik pl. 99. hozzászólás. Kár, hogy nem találtam, vagy nem található (?) szaporább keresési lehetőség! De addig is bogarászok! Üdv: epsilon
|
|
|
| [2173] epsilon | 2007-07-28 13:40:36 |
 Kedves Károly! Nem igazán szoktam döngetni ;-) meg a Fórumot sem ismerem annyira részleteiben, nem is járok régóta és túl gyakran ide, úgyhogy szerintem ülhet ott a valahol ahol van, mert biztosan nem találok rá, inkább majd szórakozásból megpróbálok magam rájönni. Üdv: epsilon
|
| Előzmény: [2170] epsilon, 2007-07-28 07:11:46 |
|
| [2172] Hajba Károly | 2007-07-28 13:28:21 |
 Üdv!
Közben az n=7 12 vonalasra találtam mégegy szigorú feltételű megoldást, így már 3-at is ismerek.
De a Csimby jelezte n=5 8 vonalasra még nem leltem rá, sőt még n=6 10 vonalast sem találtam.
|
| Előzmény: [2167] epsilon, 2007-07-27 18:13:42 |
|
| [2171] Hajba Károly | 2007-07-28 08:22:52 |
 Kedves epsilon!
Kicsit rejtélyes leszek. Nyitott kapukat döngetsz. Ti. a megoldások megtalálhatóak itt a KöMaL fórumon ... valahol. Csak meg kell keresni őket. Tudom, nem lesz nehéz, sok sikert hozzá. S ha meglelted, berakok még néhány nem-kilépő megoldást n=5, 6 tartományból.
:o)
|
| Előzmény: [2170] epsilon, 2007-07-28 07:11:46 |
|
| [2170] epsilon | 2007-07-28 07:11:46 |
 Kedves Károly! A jelzett lehetőségekről bemutatnál rajzot is, hátha további lehetőségeket tartogat? Üdv: epsilon
|
|
|
| [2168] Csimby | 2007-07-28 00:08:50 |
 Szia! Köszi az ábrákat! Az én algoritmusom most veszem észre, hogy mégsem jó, mert noha megfelelő számú szakaszból áll, az egyiket 2 részletben húzom be az pedig csalás (1 behúzással nem lehet mert van benne egy 3-fokú csúcs így muszáj abból indulni). Amúgy azt akartam, hogy az n=5-re talált "nem kilépő" megoldásomat (amit még nem akarok lerajzolni) L-alakban két szakasszal kibővítem és egy régi szakaszt meghosszabítok, ekkor n=6 egy megoldását kapom és ez folytatható is lenne, csak hát mégsem jó.
|
| Előzmény: [2167] epsilon, 2007-07-27 18:13:42 |
|
| [2167] epsilon | 2007-07-27 18:13:42 |
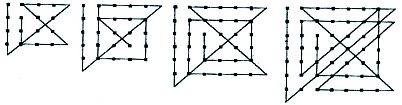
 A 328-as feladat kapcsán a következő biztos: n×n pont összeköthető 2n-2 szakaszból álló töröttvonallal, a kért feltétellel. Szemléltetés és algoritmus kialakítása végett itt egy "kép" egy pár esettel:
|
 |
| Előzmény: [2156] Csimby, 2007-07-26 23:20:32 |
|
| [2166] Hajba Károly | 2007-07-27 12:47:46 |
 A spirál alatt azt értem, hogy a mátrixot kivülröl körkörösen, majd mindig befelé haladva folyamatosan felfűztem. Ehhez, amint jól látod 1-gyel több vonal kell. Anno így határoztam meg a szükséges lépésszámot, azaz a spirálban található vonalak számából elvettem egyet. Persze később a képletet is meghatároztam. :o)
---
Az n=5 nemkilépő és visszazárón akkor elkezdek gondolkodni.
|
| Előzmény: [2164] Csimby, 2007-07-27 09:52:47 |
|
|
| [2164] Csimby | 2007-07-27 09:52:47 |
 Most látom csak hogy ez a feladat egyszer mennyire ki lett már vesézve (pl. 39.feladat), Spirálozás alatt amúgy azt érted hogy mindig az egyel kisebb oldalhosszú négyzet megoldásából állítjuk elő a következőt? Vagy mire gondolsz? Mert ugye ha csak úgy felspirálozzuk a pontokat, akkor az 1-gyel több szakasz.
|
| Előzmény: [2162] Hajba Károly, 2007-07-27 08:33:24 |
|
|




 =C1+2C2
=C1+2C2  R azaz
R azaz  i, C1
i, C1




