| [32] Hajba Károly | 2005-12-15 23:13:13 |
 G? Igen, ismert.
A probléma a valóságból való. G 3.000.000 az emberiség férfiainak létszáma; g=? a különböző fajta Y-kromoszóma száma; N 3.000.000 az emberiség férfiainak létszáma; g=? a különböző fajta Y-kromoszóma száma; N 10.000? a vizsgálatba bevont személyek száma; n=pár tucat az eddig talált különböző Y-kromoszómák száma. 10.000? a vizsgálatba bevont személyek száma; n=pár tucat az eddig talált különböző Y-kromoszómák száma.
Kérdés, hogy ismerjük-e az összes Y-kromoszómát? Ez azért érdekes, mert az emberiség elterjedésének fő vonalait felvázoló fa-struktúra csomópontjain ezek a kromoszómák ülnek és egy újabb felbukkanása részben átrajzolhatja e szerkezetet. (Az is egy érdekes eljárás, ahogyan a legnagyobb valószínűségű struktúrát kiszámolják, másrészről a mDNS hasonló elterjedést alátámasztó struktúrája megerősíti az elterjedés szerkezetét.)
Gondolom, bizonyossággal nem jelenthetjük ki, hogy nincs több, de minden újabb nem ismeretlen mintával csökken a valószínűsége ill. az elterjedtségének lehetséges mértéke. De talán az is érdekes információ lehet, ha tudjuk, hogy pl. az első 1000 mintában már szerepelt az eddig ismert elem és azóta csak ezek ismétlődnek.
|
| Előzmény: [31] Tappancsa, 2005-12-15 21:22:44 |
|
| [31] Tappancsa | 2005-12-15 21:22:44 |
 Majd gondolkozok rajta, de előbb tisztázni szeretném a kérdést. G, a golyók száma, ismert? Azt látom, hogy g nem ismert, mert különben nem lenne probléma.
Ha G nem ismert, akkor szerintem kell még plusz kikötés, hogy tetszőlegesen ritka színek nincsenek (vagy nem érdekelnek), vagyis minden szín kihúzásának a valószínűsége legalább pmin.
Anikó
|
| Előzmény: [29] Hajba Károly, 2005-12-13 23:46:32 |
|
| [30] Tappancsa | 2005-12-15 21:14:21 |
 Jól látod. Ráadásul sok más értelmes becslés létezik különböző tulajdonságokkal és csak az adott alkalmazásba belegondolva lehet eldönteni, hogy mi a fontos és melyiket használjuk.
|
| Előzmény: [28] Hajba Károly, 2005-12-13 10:19:07 |
|
| [29] Hajba Károly | 2005-12-13 23:46:32 |
 Anikó!
Te talán tudnál az alábbi már máshova betett, de válasz nélkül maradt problémámra megoldást mondani:
Adott G db golyó, melyek g féle különböző színűek, véletlenszerű eloszlásban. Mintavételezéssel N db golyóból n féle különböző szinűt ismerünk meg. (N<<G;n g) g)
Mi a valószínűsége, hogy minden golyót megismertem?
N-t mekkorára kell vennem, hogy egy bizonyos valószínűséggel kijelenthessük, nincs már több ismeretlen szinű golyó?
|
|
| [28] Hajba Károly | 2005-12-13 10:19:07 |
 Anikó!
Ha jól sejtem a két módszer közötti különbséget, akkor a több ezres mintavételezés alapján a te módszered (piros) alapján a pontos érték adódik, de nagy a szórása (nyíltartomány), míg az én módszerem (kék) nem ad pontos értéket, egy kicsit mellé tippel, de kisebb szórással.
|
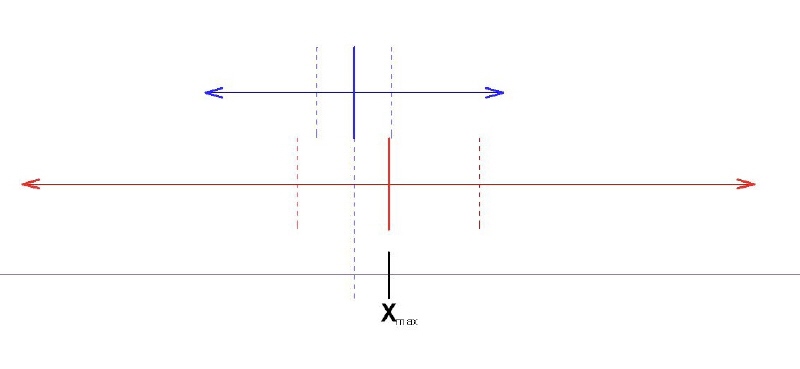 |
| Előzmény: [25] Tappancsa, 2005-12-12 17:10:00 |
|
| [27] Sirpi | 2005-12-13 09:21:23 |
 Köszi a reakcióidat, Anikó!
Igazából tanultam statisztikát az egyetemen, de attól még nem volt teljesen egyértelmű számomra sem, hogy pontosan mi is a feladat :-) Én a torzítatlan becslést találtam meg, bár végül is nagy k-kra már nincs nagy különbség az 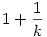 és az és az 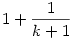 -es szorzók között. -es szorzók között.
|
| Előzmény: [20] Tappancsa, 2005-12-10 00:41:33 |
|
| [26] Hajba Károly | 2005-12-12 21:56:08 |
 Anikó!
Kezd a homály tisztulni az agyanban. :o) Én rossz képleteket vetettem egybe, mentségemül te arra a hsz-omra válaszoltál, ahol a nem 0 alsó határra adtam tippet.
[0,500] tartományra és k=500-ra 10 eset összegzésénél, már a te képleted jobb. Sajnos az EXCEL-lel nem lehet könnyedén 100.000 esetet összegezni.
Gyanítom, hogy mindegyik képlet "másként viselkedik" a különböző sűrűség ill. esetszám esetén.
De hát az örök statisztikai vicc, mit gondolom jól ismersz: "a statisztika olyan, mint a bikini, sok mindent megmutat, de a lényeget eltakarja". :o)
|
| Előzmény: [25] Tappancsa, 2005-12-12 17:10:00 |
|
| [25] Tappancsa | 2005-12-12 17:10:00 |
 Onogur! Én is csak azért ismerem ezt a témát mert a szakmámba vág (statisztikus vagyok).
Egyébként csak a (0,x) feladatra számolgattam, nem tudom, hogyan változna a képlet nem-0 alsó határ esetén. Másrészt kicsi k-val kell próbálkozni, mert különben túl közel van egymáshoz a sok becslés.
A k=3, x=3 (alsó határ 0) esetet próbáltam ki mielőtt írtam volna, 100000 ismétléssel:
Az ML-becslés: xmax-ra: átlag 2,248, négyzetes eltérés 0,906, abszolút eltérés 0,752.
A te becslésed: 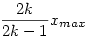 -ra: átlag 2,703, négyzetes eltérés 0,572, abszolút eltérés 0,568. -ra: átlag 2,703, négyzetes eltérés 0,572, abszolút eltérés 0,568.
A dupla-átlag: 2xátlag-ra: átlag 3,000, négyzetes eltérés 1,005, abszolút eltérés 0,815.
A torzítatlan becslés: 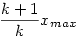 -a: átlag 3,000 (ahogy illik), négyzetes eltérés 0,600, abszolút eltérés 0,633. -a: átlag 3,000 (ahogy illik), négyzetes eltérés 0,600, abszolút eltérés 0,633.
A minimum négyzetes eltérésű becslés: 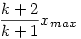 -ra: átlag 2,812, négyzetes eltérés 0,565, abszolút eltérés 0,583. -ra: átlag 2,812, négyzetes eltérés 0,565, abszolút eltérés 0,583.
Tehát az ML és a dupla-átlag becslések tényleg nem jók, és a többi úgy viselkedik, ahogy elvártam. Eddig a te becslésednek van a legkisebb abszolút eltérése. Bár 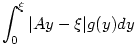 -ban optimálisan kiválasztva A-t -ban optimálisan kiválasztva A-t 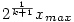 -ot kaptam (hogy ennek mi az intuíciója??), amire a "puding": átlag 2,675, négyzetes eltérés 0,582, abszolút eltérés 0,567. Mondjuk k=3-ra ez a szorzó igen közel van a tiédhez. -ot kaptam (hogy ennek mi az intuíciója??), amire a "puding": átlag 2,675, négyzetes eltérés 0,582, abszolút eltérés 0,567. Mondjuk k=3-ra ez a szorzó igen közel van a tiédhez.
Igazából a lényegi mondandóm az volt, hogy a "jó" becslés fogalma nincs jól definiálva, attól függ, hogy mi a cél.
|
| Előzmény: [24] Hajba Károly, 2005-12-12 10:45:34 |
|
| [24] Hajba Károly | 2005-12-12 10:45:34 |
 Kedves Anikó!
Én valóban nem tanultam ilyeneket (ált. gimi+BME), így csak a józan paraszti eszemre hagyatkoztam, habár nagyjából értem, amit írtál. Továbbá van egy angol közmondás: "puding próbája az evés." Nos létrehoztam egy EXCEL táblázatot és kipróbáltam mindkét változatot.
Megadtam egy alsó (10) és felső (21) értéket, majd k=600-ra generáltam véletlenszámokat ill. elkészítettem a két változat képletével a felső határ tippjét. Ezt 10-szer frissítettem és összegeztem. Sima átlagolásnál az én képletem eltérése: 0,003925, míg a tiéd: 0,021911. Ezután az értékeket a határ egyik oldalára átosztottam, ha kellett. Ekkor az enyémnél: 0,007477, míg a tiednél nem kellett, mert mind felülről közelítette. Ezután több, mint 200-ra növeltem az alsó-felső különbséget (5-300), s ezután sem változott, igaz csak szemrevételezéssel, az eredmény.
Hát akkor hol hibázhattam?
|
| Előzmény: [23] Tappancsa, 2005-12-12 01:27:56 |
|
| [23] Tappancsa | 2005-12-12 01:27:56 |
 Látom, hogy az ilyen kérdések vizsgálati módszere nem közismert tény. Nem is teljesen elemi, mert ismerni kell hozzá a sűrűségfüggvény és várható érték fogalmát, ami nem gimnáziumi tananyag. A kitalálandó x helyett  -t fogok használni, mert túl sok az 'x' a feladatban. -t fogok használni, mert túl sok az 'x' a feladatban.
Tehát, ha x1,...,xk a (0, ) intervallumból van kiválasztva, akkor az együttes sűrűségfüggvényük f(x1,...,xk)=(1/ ) intervallumból van kiválasztva, akkor az együttes sűrűségfüggvényük f(x1,...,xk)=(1/ ).....(1/ ).....(1/ )=1/ )=1/ k, ha 0 k, ha 0 xi xi  , vagyis 0 , vagyis 0 xmin és xmax xmin és xmax  , és 0 egyebütt. Tehát f felbontható egy csak az xi-ktől függő rész és csak , és 0 egyebütt. Tehát f felbontható egy csak az xi-ktől függő rész és csak  -től és xmax-tól függő rész szorzatára. Ez azt jelenti, hogy -től és xmax-tól függő rész szorzatára. Ez azt jelenti, hogy  becsléséhez xmax ismerete elégséges. becsléséhez xmax ismerete elégséges.
Innét többféleképpen mehetünk tovább. A legelterjetteb módszer, a 'maximum likelihood', azt a  0 értéket választja, aminél az xi-k valószínűsége a legnagyobb, tehát az f-et maximalizálja. Eszerint 0 értéket választja, aminél az xi-k valószínűsége a legnagyobb, tehát az f-et maximalizálja. Eszerint  0=xmax. Sajnos a módszer összes jó tulajdonsága akkor érvényes, ha f differenciálható 0=xmax. Sajnos a módszer összes jó tulajdonsága akkor érvényes, ha f differenciálható  0-nál, a mi f-ünk pedig nem is folytonos. 0-nál, a mi f-ünk pedig nem is folytonos.
Mivel xmax intuitíve nem nyerő, próbálhatunk javítani rajta. Számoljuk ki a várható értékét, ehhez kell a sűrűségfüggvénye, amit az eloszlásfüggvényéből tudunk kiszámolni: G(y)=Val(xmax y)=Val(x1 y)=Val(x1 y).....Val(xk y).....Val(xk y)=(y/ y)=(y/ )k, ahol Val-lal jelöltem a valószínűséget. Ebből a sűrűségfüggvényt deriválással kapjuk: g(y)=kyk-1/ )k, ahol Val-lal jelöltem a valószínűséget. Ebből a sűrűségfüggvényt deriválással kapjuk: g(y)=kyk-1/ k, ahol 0 k, ahol 0 y y  . Tehát xmax várható értéke . Tehát xmax várható értéke 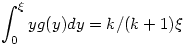 , ha jól számoltam. Így (k+1)/k.xmax várható értéke pont , ha jól számoltam. Így (k+1)/k.xmax várható értéke pont  , tehát egy torzítatlan becslést ad. , tehát egy torzítatlan becslést ad.
Ha a várható eltérés négyzetét akarjuk minimalizálni, akkor keresgélhetünk az A.xmax alakú becslések között. 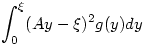 -t kell minimalizálni. Így kaptam (k+2)/(k+1).xmax-et. -t kell minimalizálni. Így kaptam (k+2)/(k+1).xmax-et.
Nem tudom mennyire lehet ezt a magyarázatot megérteni friss szemmel, szívesen részletezem, ha érdekel valakit.
Anikó
|
| Előzmény: [22] Hajba Károly, 2005-12-10 23:41:35 |
|
|
| [21] Hajba Károly | 2005-12-10 01:34:08 |
 Üdv!
Úgy látom, hogy felvetésed sokunk fantáziáját megmozgatta.
Tegyük fel, hogy a véletlenszámok teljesen egyenletesen oszlanak el. Ekkor gyakorlatilag egy 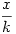 tartomány közepén ülnek. Azaz tartomány közepén ülnek. Azaz 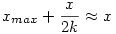 Innen Innen 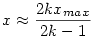 . .
|
| Előzmény: [15] Sirpi, 2005-12-08 16:41:35 |
|
| [20] Tappancsa | 2005-12-10 00:41:33 |
 A legjobb becslés természetesen attól függ, hogy mi a "jó" definíciója. (k+1)/k.max (xi) egy torzítatlan becslés (vagyis hosszú-távon átlagosan x-et ad), ami persze jó. De ha a várható eltérés négyzetét akarod minimalizálni, akkor (k+2)/(k+1).max (xi) jobb (nem tudom, hogy a legjobb-e, bár valószínűleg az), de nem torzítatlan. Tehát, neked mitől jó egy becslés?
Anikó
|
| Előzmény: [15] Sirpi, 2005-12-08 16:41:35 |
|
| [19] jenei.attila | 2005-12-09 12:23:53 |
 Előbb kicsit meggondolatlan voltam. Nyilvánvaló, hogy x a maximális mintaelemnél nem lehet kisebb. Másrészt minél több a mintaelem,annál kevésbé valószínű, hogy a maximális elemnél lényegesen nagyobb legyen az x. Vagyis x a maximális mintaelem, plusz valami kis d intervallum (ahol pl. d= a szomszédos mintaelemek közötti távolságok átlagának fele). Egyelőre ez csak találgatás, még gondolkozok.
|
| Előzmény: [18] jenei.attila, 2005-12-09 10:41:47 |
|
|
|
| [16] 2501 | 2005-12-09 00:41:57 |
 Igy elso olvasasra 2*atlag(x1,x2,...,xk).
|
|
| [15] Sirpi | 2005-12-08 16:41:35 |
 Sziasztok!
Van egy (saját) valszám problémám, úgy láttam, ide lenne a legjobb beírni. Szóval gondolok egy x pozitív valós számra, és titokban tartom. Viszont generálok [0,x]-en egyenletes eloszlással, egymástól függetlenül k db. számot (x1, x2, ..., xk), és ezeket megmondom. Ezekből kellene x-re jó becslést adnunk. Mi legyen ez? (Van ötletem, de senkit nem akarok befolyásolni)
Mi van akkor, ha [x,y]-ból generálom az értékeket ismeretlen határokkal?
|
|
| [14] Tamás | 2005-10-04 10:32:50 |
 Sziasztok! Lenne egy kis valószínűségszámítási kérdésem. Nem vagyok egy matek zseni úgyhogy elnézést kérek előre is, azoktól akiknek egyszerűnek tűnik a kérdés. Idézet Székely J. Gábor könyvéből:" Tudjuk már, hogy akármilyen sok fejet is dobunk egymás után, a soron következő feldobáskor semmivel sem lesz nagyobb az irás esélye. Ezek után felvetődik a kérdés:maximálisan milyen hosszú egymás utáni fejdobásokból álló ½tiszta fej½ blokkra kell számítanunk egy n hosszúságú dobássorozatban? Száz dobásnál 6-7,ezer dobásnál 9-10, egymilliónál pedig körülbelül 19-20 hosszúságú tiszta fej blokk várható. Erdős Pál és Rényi Alfréd általánosan bebizonyították, hogy nagyszámú dobás között nagy valószínűséggel elő kell fordulnia egy log2 n hosszúságú "tiszta fej" blokknak." A fej-irás játéknál 50-50 százalák mindkét oldal valószínűsége! A kérdésem az lenne hogyan számítható ez ki, egy olyan játéknál ahol nem egyenlőek a valószínűségek. Pl.: belerakok egy "kondérba" 1 piros és 3 fehér golyót. Ugyebár annak a valószínűsége hogy pirosat húzok 1/4 és hogy fehéret 3/4. Körülbelül milyen hosszú ( természetesen minden egyes húzás után visszateszem a golyót ) tiszta piros illetve fehér blokkra kell egy ilyen típusú játéknál számítani n húzás során?
Előre is köszönöm. Üdv. T.
|
|
| [13] lorantfy | 2005-04-08 16:39:55 |
 Én hobbiból írtam már tetrisz játékot - nagyon jó móka volt. Először véletlenszerűen generáltattam a programmal a különböző lehetséges alakzatokat. Aztán rájöttem, hogy túl könnyű, mivel elég sokszor ad 1-es négyzetet.
Ezután egyre nehezedő szinteket állítottam be, hogy a könyebb alakzatok egyre ritkábban jöjjenek. Mondjuk 1 és 100 között generáltattam számokat, aztán megadtam milyen határok között milyen alakzatot dobjon le. Ezek a határok szintenként változtak.
|
| Előzmény: [12] ScarMan, 2005-04-08 14:26:56 |
|
| [12] ScarMan | 2005-04-08 14:26:56 |
 A tetrisz (egyszerű, kézi játékra gondolok) véletlenszerűen hozza le az alakzatokat, vagy sok, előre betáplált sorrendje van? Ha vélétlen, akkor hogy generálja?
|
|
| [11] 2501 | 2005-03-31 16:20:16 |
 "The VIA C3 Nehemiah processor includes a high-performance hardware-based random number generator (RNG) on the processor die."
Más:
"Modern superscalar processors feature a large number of hardware mechanisms which aim at improving performance: caches, branch predictors, TLBs, long pipelines, instruction level parallelism, ... The state of these components is not architectural (i.e. the result of an ordinary application does not depend on it), it is also volatile and cannot be directly monitored by the user. On the other hand, every invocation of the operating system modifies thousands of these binary volatile states.
HAVEGE (HArdware Volatile Entropy Gathering and Expansion) is a user-level software unpredictable random number generator for general-purpose computers that exploits these modifications of the internal volatile hardware states as a source of uncertainty."
http://www.irisa.fr/caps/projects/hipsor/HAVEGE.html
Le is fordítom:
"A VIA C3 Nehemiah processzor magja nagyteljesítményű véletlenszám-generátort tartalmaz."
"A modern szuperskalár processzorok nagy számú, a teljesítmény növelésére irányuló berendezést tartalmaznak, úgy mint gyorsítótárak, ugrás-előrejelzők, lapozási segédtáblák, hosszú futószalagok, utasításszintű párhuzamosság, stb. Ezen részek állapota nem architekturális (egy szokványos alkalmazás eredménye független tőle), továbbá gyorsan változó és közvetlenül nem megfigyelhető. Másrészről viszont minden egyes operációsrendszer-hívás ilyen bináris állapotok ezreit módosítja.
A HAVEGE (ezt inkább nem fordítanám le :o) egy felhasználói szintű szoftveres nemkiszámítható-véletlenszám-generátor általános célú számítógépekre, amely a hardver belső állapotainak ilyetén változásait használja a kiszámíthatatlanság forrásaként."
|
|
| [10] Doom | 2005-03-29 22:04:31 |
 Igen, ez engem is felettéb érdekelne...
Egy nem megbízható forrásból úgy hallottam, hogy egy jó bonyolult műveletsort hajtanak végre, ami a gép kerekítése miatt nem mindig lesz ugyannnyi... de hogy miért nem, arról fogalmam sincs.
|
| Előzmény: [9] BrickTop, 2004-11-01 10:56:33 |
|
| [9] BrickTop | 2004-11-01 10:56:33 |
 Egyszerű számítógépes programokban gyakran használják a gépidőt vagy az adott program futásidejét a véletlenszám-generálás alapjának.
Engem az érdekelne, hogy a számológépek hogyan gyártják a véletlenszámokat? Milyen értéket vesznek alapul? Nincs bennük óra, és egy Reset után nem ugyanazokat a számokat adják. Nekem ötletem sincs.
|
| Előzmény: [8] Kós Géza, 2004-10-25 12:28:13 |
|
| [8] Kós Géza | 2004-10-25 12:28:13 |
 Nem a hardver a lényeg, hanem, hogy külső "zajokat" is figyelembe vesz, pédául az utolsó billentyű lenyomásának hosszát. Azonban az ilyen zajok csak korlátozott mennyiségben állnak rendelkezésre.
Ha gyorsan, sok véletlenszámra van szükség, akkor muszáj álvéletlen sorozatokat gyártani. Ha viszont a sebesség kevésbé számít és sokkal fontosabb a biztonság, akkor marad a hardver zaj meg a dobókocka.
Pacepa könyve szerint Ceausescu idejében a román titkosszolgálat -- véletlen titkosító kulcsok készítéséhez -- vett egy véletlenszámokat gyártó gépet, de nem bíztak meg benne, ezért inkább dobókockát használtak. :-)
|
| Előzmény: [7] Tamás, 2004-10-23 09:28:39 |
|
