| [9] Csimby | 2004-11-15 19:34:04 |
 Az Ankéton a gráfos előadáson elhangzott egy gráfos megoldás a 3. feladatra. Sajnos én akkor iszonyatosan álmos voltam, és ezért nem emlékszem rá, de ha valaki emlékszik, szerintem érdemes lenne beírni. Egyébként asszem az előadó azt mondta, hogy az előadás teljes anyaga fel lesz rakva a KöMaL honlapjára.
|
|
| [8] Kós Géza | 2004-10-29 10:53:20 |
 Erben Péter hívta fel rá a figyelmemet, hogy majdnem ugyanez volt az 1978-as olimpia 4. feladata:
Az ABC háromszögben AB=AC. Egy kör belülről érinti az ABC háromszög köré írt kört, továbbá az AB oldalt a P, az AC oldalt a Q pontban. Bizonyítsuk be, hogy a PQ szakasz felezőpontja az ABC háromszög beírt körének középpontja.
|
| Előzmény: [7] Kós Géza, 2004-10-29 10:47:15 |
|
| [7] Kós Géza | 2004-10-29 10:47:15 |
 Van egy rövid inverziós megoldás is.
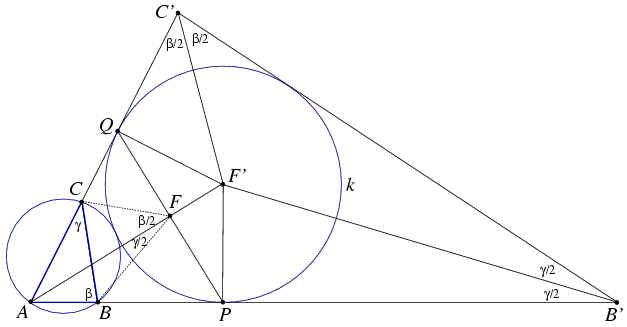
Alkalmazzunk inverziót az A középpontú, AP=AQ sugarú körre. A B, C, F pontok képe legyen B', C', illetve F'. A k kör képe önmaga, a körülírt kör képe a B'C' egyenes, ezek szintén érintik egymást.
A befogótételből következik, hogy F' éppen a k kör középpontja.
Az ABC és AC'B' háromszögek hasonlók, innen AB'C' = = és AC'B' és AC'B' = = . Az AB'C' háromszögben k éppen a beírt kör, tehát B'F' és C'F' szögfelezők. . Az AB'C' háromszögben k éppen a beírt kör, tehát B'F' és C'F' szögfelezők.
Az ABF és AF'B' , illetve ACF és AF'C' háromszögek is hasonlók, így 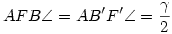 és és 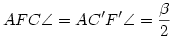 . .
Az ABF és ACF háromszögek szögeit összeszámolva kapjuk, hogy BF és CF éppen az ABC háromszög külső szögfelezői.
|
 |
| Előzmény: [5] Kemény Legény, 2004-10-28 16:59:30 |
|
| [6] Kós Géza | 2004-10-29 10:18:33 |
 A 3. feladat valószínűleg onnan származik, hogy valaki transzformációk szorzatával játszott.
A pontok jelentsék a sík geometriai transzformációit, nevezetesen a kék pont jelentsen tükrözést az x-tengelyre, a piros pont pedig jelentsen origó körüli, 120o-os forgatást. Minden egyes helyzetben szorozzuk össze, avagy alkalmazzuk egymás után a transzformációkat a teljes körön.
Két kék pont esetén a szorzat mindig az identitás, akárhonan kezdjük a transzformációkat összeszorozni és ez a tulajdonság minden lépésnél megmarad.
Két piros pont esetén viszont a szorzat nem az identitás. A két kék pontból indulva tehát nem lehet a két piros pontot elérni, és fordítva.
A megoldás elmondható transzformációk nélkül is, ahogy azt már láttuk. A kék pontok száma mindig páros, és a kört páros sok ívre osztják. Ha minden második íven megszámoljuk a piros pontokat, és minden elsőn is, a kétféle összeg különbsége 3-mal osztva vagy mindig 0, vagy mindig  1 maradékot ad. 1 maradékot ad.
|
| Előzmény: [4] BohnerGéza, 2004-10-28 14:25:12 |
|
| [5] Kemény Legény | 2004-10-28 16:59:30 |
 Az 1. feladatra gyors megoldás adható Casey tételének segitségével.Casey tétele:Adott egy k kör és 4 másik kör (k(1),k(2),k(3),k(4)),amelyek érintik a k kört.Ekkor e(12)e(34)+e(23)e(41)=e(13)e(24) ,ahol e(ij) az a k(i) és a k(j) körök közös érintőszakaszának a hossza,mégpedig a külső érintőt kell venni,ha a két kör k ugyanazon oldalán van.egyébként pedig a belső érintőszakaszt kell venni.(Ez a Ptolemaiosz-tétel egyfajta általánositása is).A Kürschák-feladatban pedig 3 pontkör van(a 3 csúcs),ill.a megadott speciális tulajdonságú kör,az alapkör pedig a köréirt kör.Az érintőszakaszok számolhatóak a Casey-tételből,igy AP hossza könnyen meghatározható a háromszög oldalaiból.Innen pedig már egyszerü a befejezés...
|
|
| [4] BohnerGéza | 2004-10-28 14:25:12 |
 A harmadik feladat megoldásával a Nehezebb matematikai problémák téma [96.], [103.] és [104.] hozzászólása foglalkozik.
|
|
| [3] BohnerGéza | 2004-10-21 14:41:24 |
 Az 1. feladat: Adott a síkban az ABC háromszög, melynek köréírt körét kívülről érinti a k kör. A k kör érinti egyúttal az AB és AC félegyeneseket is, mégpedig P és Q pontban. Mutassuk meg, hogy a PQ szakasz felezőpontja egybeesik az ABC háromszög BC oldalához hozzáírt körének középpontjával.
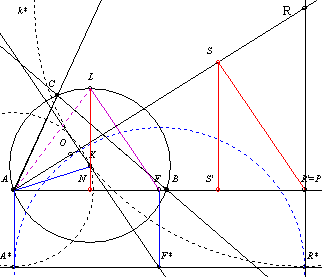
1. feladat egy megoldása. Legyen k középpontja R, a körülírté K, ennek sugara r, valamely pontnak az AB-re eső merőleges vetületét vesszősen jelöljük. (Ezért a P=R')
Szerkesszük meg R-t! R az alfa f szögfelezőjén van, egyforma távol az AB egyenestől és a körülírt körtől. Ha a k sugarát r-rel megnöveljük, az új kör (k*) átmegy K-n és érinti az AB-től r-rel 'lejjebb'; lévő v (vezér)egyenest. A pontok v-re eső merőleges vetületét csillaggal jelöljük. Az f-en lévő R tehát olyan körnek a kp-ja, mely átmegy K-n és érinti v-t. Ezen feltételeknek az A is megfelel egy r sugarú kör kp-jaként. Ennek és a keresett k*-nak a hatványvonala az A-n átmenő f-re merőleges g egyenes, így g és v metszéspontja (F*) egyenlő távol van A*-tól és R*-tól. Mivel A* adott, R*, R'és R szerkeszthető.
Határozzuk meg az AR' távolságot! Először toljuk r-rel 'fel' a KF* szakaszt, ez az LF lesz. Többször kihasználjuk majd, hogy a csúcs, érintőkör középpont, érintési pont által meghatározott háromszög hasonló a szereplő háromszögekhez.
AR'= 2 AF, AF= AN+NF, AN=c/2, NF/NL =ró/(s-a) és NL/AN=(s-c)/ró,
e két utóbbi szorzata NF/AN=(s-a)/(s-c), ezekből
AF=bc/(2(s-a)), tehát AR' = bc/(s-a)
Határozzuk meg az AS' távolságot! Ha ez s, akkor S az érintőkör kp-ja. Két hasonlóságból adódik, hogy AS'=(AS/AR')*(AS/AR')*AR'. Ez így is írható:
AS' = [(s-a) / AO] * [s / AOa] * AR' A Fórum/GEOMETRIA téma 41. feladatát használva valóban AS'= s adódik.
|
 |
| Előzmény: [1] KiCsa, 2004-10-12 17:53:05 |
|
| [2] Edgar | 2004-10-13 00:33:11 |
 Régebbi Kürschák-feladatok feszítenének esetleg?
Ez egy igazán zsír oldal, ahol mások mellett a Kürschák-verseny összes valaha volt feladata is fesszent. Aki alapszinten nyesi angolt az sassolja meg >=1x!
|
|
| [1] KiCsa | 2004-10-12 17:53:05 |
 A Kürschák példák szerintem igazán megérdemelnek egy saját témát. Az igaz, hogy pár megoldás már olvasható a Nehezebb matematikai problémák cím alatt, de a feladatok nem találhatóak sehol és ez kellemetlen azoknak, akik nem ismerik a példákat. A megoldásgyűjtögetést is jobb lenne itt folytatni...
A 2004. évi Kürschák József Matematikai Tanulóverseny feladatai
1. feladat:
Adott a síkban az ABC háromszög, melynek köréírt körét kívülről érinti a k kör. A k kör érinti egyúttal az AB és AC félegyeneseket is, mégpedig P és Q pontban. Mutassuk meg, hogy a PQ szakasz felezőpontja egybeesik az ABC háromszög BC oldalához hozzáírt körének középpontjával.
2. feladat:
Határozzuk meg a legkisebb olyan, 2004-től különböző, pozitív egész n számot, amelyhez létezik olyan egész együtthatós f(x) polinom, hogy az f(x)=2004 egyenletnek legalább egy, az f(x)=n egyenletnek pedig 2004 különböző egész megoldása van.
3. feladat:
Egy körvonal mentén néhány kék és piros pontot helyeztünk el. Ezekkel az alábbi műveleteket végezhetjük:
(a) valahova beillesztünk egy új piros pontot, és a két szomszédját ellentétes színűre változtatjuk.
(b) Ha legalább három pont van, és ezek közül legalább az egyik piros, akkor egy piros pontot törlünk, a két szomszédját pedig ellentétes színűre változtatjuk.
Kezdetben két kék pont van a kör kerületén, mindkettő kék. Elérhetjük-e a lépések többszöri alkalmazásával, hogy újra két pontunk legyen, de azok pirosak legyenek?
|
|
