| [1110] Maga Péter | 2010-04-11 16:01:03 |
 Vagy mondhatjuk azt, hogy nem a zn-1=(z-e0).....(z-en-1), hanem a zn-1+...+z+1=(z-e1).....(z-en-1) azonosságba helyettesítünk z=1-et. Ezzel nem használunk folytonosságot.
|
| Előzmény: [1108] nadorp, 2010-04-07 11:08:02 |
|
| [1109] Marika | 2010-04-11 15:44:20 |
 Sziasztok ! Valaki segítene megoldani?
Egy háromszög oldalfelező pontjai (-2;-2),(5;1),(3;4) a, Számítsuk ki a háromszög csúcsainak koordinátáit. b,Számítsuk ki az eredeti és a z oldalfelező pontok által meghatározott háromszögek súlypontjainak koordinátáit. Mit tapasztalunk?
És még egy lenne
Az ABC háromszög A csúcsának helyvektora a/vektor/(-2;3),AB/vektor/=7i-2jés CB/vektor/=3i-6j Számítsuk ki a háromszög csúcsainak és súlypontjának koordinátáit.
Lécci segítsetek megoldani de ha lehet magyarázattal, hogy utána egyedül is sikerüljön. Előre is köszönöm a segítséget!!!!!!!!!
|
|
|
| [1107] HoA | 2010-04-07 08:53:11 |
 A Geometria [1404] –ben kitűzött feladat szerepel Reiman István „Geometria és határterületei” és „Fejezetek az elemi geometriából” könyveiben. A megoldás ötlete az, hogy a komplex síkon az n-ik egységgyököket feleltessük meg a szabályos n-szög csúcsainak. Ezek az ei egységgyökök a zn=1 egyenlet megoldásai, a P=zn-1=0 polinom nullhelyei, ahol e0=1. Ezért a polinom felírható P=(z–1)(z–e1)...(z–en-1) alakban. Ugyanakkor zn-1=(z–1)(zn-1+zn-2+...+z+1) Mindkét kifejezést z-1 tényezővel osztva az adódó kifejezések z=1 helyen vett abszolútértékére adódik, hogy |(1–e1)|.|(1–e2)|...|(1–en-1)|=1+1+..+1=n és itt a baloldal éppen a z=1 csúcsból a többi csúcsba húzott átlók hosszának szorzata.
A kérdés: „Középiskolában tanultuk”, hogy egy ilyen z-1 -gyel történő egyszerűsítés után a továbbiakban ki kell kötnünk, hogy z 1 . Itt pedig a folytatásban éppen a z=1 helyen nézzük a dolgokat. Nem hiányzik itt valami? 1 . Itt pedig a folytatásban éppen a z=1 helyen nézzük a dolgokat. Nem hiányzik itt valami?
|
|
|
|
|
|
| [1102] K Robi | 2010-04-03 19:41:56 |
 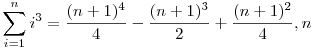 természetes szám. természetes szám.
Meg tudná valaki mutatni a bizonyítását? Természetesen egy link is tökéletesen megfelelő olyan helyre, ahol megtalálom (lehetőleg magyar vagy angol vagy német nyelven).
|
|
| [1101] Maga Péter | 2010-03-29 08:52:14 |
 A bizonyítás ,,helyből'' valóban nem könnyű. Van azonban egy valós függvénytani elmélet, aminek ez az egyik első alkalmazása. Lényegében azt lehet bebizonyítani, hogy egy valós-valós függvény folytonossági pontjainak halmaza előáll megszámlálható sok nyílt halmaz metszeteként (ez egyszerű következménye a folytonosság definíciójának); a racionális számok halmaza pedig nem (ez pedig következik Baire kategóriatételéből).
|
| Előzmény: [1100] jonas, 2010-03-28 13:30:57 |
|




 1 esetén f(z)=zn-1+...+z+1, de mivel a jobb oldal mindenhol folytonos, ezért f(1) a jobb oldal z=1 helyettesítési értékével értelmezhető
1 esetén f(z)=zn-1+...+z+1, de mivel a jobb oldal mindenhol folytonos, ezért f(1) a jobb oldal z=1 helyettesítési értékével értelmezhető


