Fórum: Valaki mondja meg!

Szeretnél hozzászólni? Jelentkezz be.

[1191] Sirpi	2010-05-24 00:20:10
641\|2^2⁵+1, sőt, 4 fölött nem találtak még olyan kitevőt, ami prímet eredményezne. Bővebben.
Előzmény: [1190] Hölder, 2010-05-23 23:49:40

[1190] Hölder	2010-05-23 23:49:40
Sziasztok! Azon gondolkodtam el,hogy ha 2(n)+1 prim (kitevőben van az n), akkor n kettő hatvány (Fermat primek),de forditva igaz -e, azaz, ha n kettőhatvány,akkor 2(n)+1 prim, megnéztem egy jó ideig,addig igaz volt,az a sejtésem, hogy nem az.

2010-05-22 10:41:45

Páros k-ra:

$\zeta(k)=-\frac{(2\pi i)^k}{2k!}B_k.$

Itt B_k a Bernoulli-szám, a következő hatványsor normált együtthatóiból adódik:

$\frac{x}{e^x-1}=\sum_{k=0}^{\infty}B_k\frac{x^k}{k!}.$

Forrás: H. Iwaniec, Topics in Classical Automorphic Forms, Amer. Math Soc. (1997), 12. oldal.

[1188] jenei.attila	2010-05-22 08:30:18
Jogos a kiegészítés, köszönöm szépen. Erre gondoltam én is, csak kicsit pontatlanul fogalmaztam. Páros kitevőkre az a bizonyos racionális szám hogyan adható meg k függvényében? Igazából arra gondoltam, hogy erre létezik egy zárt képlet. Meglehet, hogy $\zeta$ (3) rac. együtthatós polinomjaként kifejezhető páratlan k-kra is $\zeta$ (k).
Előzmény: [1184] Maga Péter, 2010-05-21 11:43:15

[1186] Róbert Gida	2010-05-21 18:52:28
$\zeta$ (3)-ról 1979-ben bizonyította be Apéry, hogy irracionális.
Előzmény: [1184] Maga Péter, 2010-05-21 11:43:15

[1185] jonas	2010-05-21 11:56:08
A Poisson közelítést a binomiális eloszlásra akkor lehet használni, ha várhatóan kevés rossz üveg készül, például abban az esetben, amit Sirpi javasolt.
Előzmény: [1182] Yvi, 2010-05-20 23:38:21

[1184] Maga Péter	2010-05-21 11:43:15
A páros esetben $\zeta$ (2k)= $\pi$ ^2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen $\zeta$ (3), $\zeta$ (5),... a kérdéses értékek, ezek tetszőleges pontossággal kiszámolhatók, akár a $\pi$ , az e, a $\gamma$ (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a $\zeta$ páratlan értékei, illetve ha nem, akkor esetleg más konstansokkal ( $\pi$ , e stb.) összefüggésbe hozhatók-e. 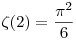A $\gamma$ -ról sem tudjuk, hogy racionális-e, és azt sem tudjuk, hogy $\pi$ +e racionális-e (ha az lenne, akkor az e ugyanúgy kifejezhető lenne a $\pi$ -ből, mint a $\zeta(2)=\frac{\pi^2}{6}$ ), mégsem használjuk egyikre sem, hogy nem ismert.
Előzmény: [1176] jenei.attila, 2010-05-20 19:36:13

[1183] SmallPotato	2010-05-21 00:08:08
No, azért nem egészen "kevésbé ismert még az az összefüggés", hogy mennyi is a négyzetszámok reciprokösszege :-)
Előzmény: [1173] D. Tamás, 2010-05-20 19:08:29

[1182] Yvi	2010-05-20 23:38:21
A binomiális eloszlással hogy jött ki a 803? Tényleg nem Poisson, csak elnéztem, az volt, oda írva, hogy a Poisson közelítést kell használni. Ez jelenti azt, hogy np=lambda?
Előzmény: [1177] jonas, 2010-05-20 21:39:13

Már regisztráltál?
Új vendég vagy?