|
| [16] philip | 2005-12-04 09:18:54 |
 Erre valaki tud valami okosat mondani...nagyon megköszönném!
|
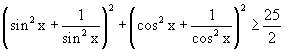 |
|
| [15] Lóczi Lajos | 2005-11-22 14:32:09 |
 Olyan formában nem, ahogy írtad, de ha valamelyik tényező egy derivált, akkor igen, pl. n=3-ra:
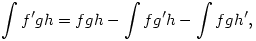
ami persze csak a szorzat deriválási szabálya 3-tényezős szorzatokra.
|
| Előzmény: [14] Wolf, 2005-11-22 12:25:18 |
|
| [14] Wolf | 2005-11-22 12:25:18 |
 Mikor még tanultuk a parciális integrálást, két függvény szorzatát bontottuk fel, de létezik-e több fv szorzatára ilyen módszer?
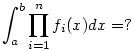
Köszönöm
|
|
|
| [12] Lóczi Lajos | 2005-11-22 01:06:42 |
 Persze, hogy létezik a limsup, de a limesz létét is el lehet érni, és egy limeszt könnyebb "látni". Az én példámban a teljes tér a [0,1] intervallum volt (nem volt feltétel, hogy az egész számegyenes legyen).
Bár egyik példa sem ad választ az eredeti kérdésre: ő megszámlálhatóan végtelen sok értékre kérdezett rá :)
|
| Előzmény: [11] Róbert Gida, 2005-11-21 23:53:20 |
|
| [11] Róbert Gida | 2005-11-21 23:53:20 |
 Szia Yoteky!
Ez Czách egyik kedvenc példája az 1. féléves analízis vizsgán. Persze senki nem tudja rá a választ, de nem kell aggódni, mindenkinek elmondja a függvényét.
A feladat pontosan : minden pozitív hosszú intervallumon a függvény minden valós értéket felvesz. A megoldás, ha jól emlékszem rá:
Legyen tetszőleges x valós számra 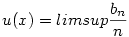 , ahol bn jelöli, hogy az x törtrészében az első n bináris jegye közül hány darab 1 van. Ekkor nyilván 0 , ahol bn jelöli, hogy az x törtrészében az első n bináris jegye közül hány darab 1 van. Ekkor nyilván 0 u(x) u(x) 1 teljesül, továbbá könnyű igazolni, hogy minden pozitív hosszú intervallumon az u függvény minden 0 és 1 közti értéket felvesz. Most már csak ezt a [0,1] intervallumot kell a valós számok intervallumára transzformálni. Ez sokféleképp lehetséges, egy példa rá: legyen a keresett f függvény 1 teljesül, továbbá könnyű igazolni, hogy minden pozitív hosszú intervallumon az u függvény minden 0 és 1 közti értéket felvesz. Most már csak ezt a [0,1] intervallumot kell a valós számok intervallumára transzformálni. Ez sokféleképp lehetséges, egy példa rá: legyen a keresett f függvény 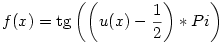 , ekkor viszont baj van u(x)=0;1 esetén, ezekben a pontokban legyen f például nulla. Ekkor az előbbiek miatt az f függvény minden pozitív hosszú intervallumon minden valós értéket felvesz. , ekkor viszont baj van u(x)=0;1 esetén, ezekben a pontokban legyen f például nulla. Ekkor az előbbiek miatt az f függvény minden pozitív hosszú intervallumon minden valós értéket felvesz.
Oh most látom hogy már érkezett is megoldás.
Kedves Lajos: a [0,1] intervallumbeli értékeket veszi csak fel minden pozitív hosszú intervallumon a te függvényed! Ez nálam az u függvény. Továbbá a limsup az mindig létezik!
|
| Előzmény: [9] Yoteky, 2005-11-21 22:55:02 |
|
| [10] Lóczi Lajos | 2005-11-21 23:25:44 |
 Tekintsük pl. a [0,1] intervallumot, és benne írjuk fel a számokat pl. kettes számrendszerben, x=0,x1x2x3.... Ekkor legyen 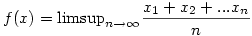 . Ez jó lesz: minden részintervallumban felvesz minden értéket [0,1] között. . Ez jó lesz: minden részintervallumban felvesz minden értéket [0,1] között.
Az első néhány bináris jegy dönti csak el, hogy x belekerüljön egy tetszőleges részintervallumba, de ez a limsup-ra nyilván nincs hatással. Utána meg tudom választani az xi jegysorozatot, hogy a limesz is létezzen és tetszőleges előre megadott [0,1]-beli értékkel legyen egyenlő.
|
| Előzmény: [9] Yoteky, 2005-11-21 22:55:02 |
|
| [9] Yoteky | 2005-11-21 22:55:02 |
 Haliho Mindenki! Lenne egy kérdésem amiben szeretném a segítségeteket kérni: Melyik az a függvény amely minden intervallumon minden (megszámlálhatóan végtelen) értéket felvesz. A segítséget előre is köszi! Yoteky
|
|
| [8] na akkor | 2005-10-18 00:41:58 |
 Mindenkinek köszönöm a segitségét és elnézést hogy több topicba írtam csak féltem hogy nem érkezik válasz :) Köszönöm mégegyszer!
|
|



 4sin2xcos2x
4sin2xcos2x 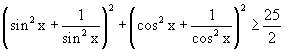



 u(x)
u(x)