| [178] Lóczi Lajos | 2007-03-22 16:45:18 |
 A "többdimenziós mátrixokat" szokás tenzoroknak vagy multilineáris leképezéseknek nevezni (melyek bizonyos transzformációs szabályoknak engedelmeskednek). A multilineáris leképezés olyan, hogy több vektorhoz rendel egy számot, és mindegyik változójában lineáris. A fizikában, differenciálgeometriában, analízisben (pl. R2 R2 függvények magasabbrendű deriváltjai multilineáris leképezések) sokszor használatosak. R2 függvények magasabbrendű deriváltjai multilineáris leképezések) sokszor használatosak.
Néhány keresőszó:
multilinear algebra, multilinear form, tensor, tensor product. Két példa:
http://documents.wolfram.com/v5/Built-inFunctions/ListsAndMatrices/StructureManipulation/FurtherExamples/Inner.html
http://documents.wolfram.com/v5/Built-inFunctions/NumericalComputation/MatrixOperations/FurtherExamples/Outer.html
|
| Előzmény: [175] Willy, 2007-03-22 12:00:54 |
|
| [177] jenei.attila | 2007-03-22 14:15:55 |
 Tudtommal nem léteznek, ugyanis a mátrix nem egy téglalap sémába rendezett számcsoport (csak annak látszik). Lényegében a mátrix véges dimenziós vektortéren értelmezett korlátos lineáris operáció, amely szintén véges dimenziós vektortérbe képez. Ez röviden azt jelenti, hogy ha L az operáció, akkor L(a+t*b)=L(a)+t*L(b) minden a,b vektortérbeli elemre és minden t valós számra (ha a valós számtest feletti vektortérről van szó). Egy ilyen operáció reprezentálható egy mátrixszal, amelynek oszlopai megadják, hogy az L operáció értelmezési tartományának bázisvektorai az L által milyen vektorba képeződnek. Az általad ismert mátrixszorzás pedig nem más, mint az általuk reprezentált operációk egymás utáni alkalmazása által nyert operáció mátrix reprezentánsa. A mátrix összeadás pedig az operációk egyszerű függvény összeadása (természetesen a vektortérbeli összeadás szerint). Látható, hogy a téglalap séma csak technikai könnyítés (jelölés), és nem tartozik a mátrix lényegéhez.
|
| Előzmény: [175] Willy, 2007-03-22 12:00:54 |
|
| [176] HoA | 2007-03-22 14:06:25 |
 Valóban, a legegyszerűbben a Sirpi által leírt módon, tehát pihagoraszi számhármasok "átfogóinak" összeszorzásával lehet ilyen számokat találni. De példád éppen arra mutat rá, hogy nemcsak ilyen megoldások vannak, és talán ezek az érdekesebbek.
A szorzásos módszerrel 65 = 5 * 13, vegyük tehát a (3,4,5) és (5,12,13) hármasokat, ezekből adódik (39,42,65) és (25,60,65). A primitív pithagoraszi hármasokat előállító képlet szerint (x2-y2,2xy,x2+y2) 65-öt mint két primitív "átfogó" egészszám-szorosát kapjuk: 13.(22+12) illetve 5.(32+22)
A Te példádban a 65 két primitív pithagoraszi hármas átfogójaként áll elő: x=8, y=1 választással (63,16,65), ahol 65=82+12, illetve x=7, y=4 választással (33,56,65) - és nem 53 - , ahol 65=72+42
Érdekes lenne bizonyítani, hogy végtelen sok szám áll elő többféleképpen két relatív prím négyzetszám összegeként, illetve hogy bármilyen n-re vannak olyan számok, melyek n féleképpen állíthatók elő két relatív prím négyzetszám összegeként.
|
| Előzmény: [173] Borgi - Tóth Áron, 2007-03-21 22:05:13 |
|
| [175] Willy | 2007-03-22 12:00:54 |
 Nem tudom, hogy ide tartozik-e vagy nem, de:
Léteznek-e több dimenziós mátrixok a matematikában, és ha igen, akkor mire és hogyan lehet őket használni (pl. két 3D mátrixot hogyan lehet összeszorozni, vagy mi a determinánsa)?
|
|
| [174] Sirpi | 2007-03-21 22:41:45 |
 Jól érzed :-)
Vegyünk pithagoraszi számhármasokat, pl:
32+42=52
122+52=132
202+212=292
Az elsőt beszorozva (13.29)2-nel kapjuk, hogy
(3.13.29)2+(4.13.29)2=(5.13.29)2
Ugyanígy a 2.-at és a 3.-at is megfelelően megszorozva:
(12.5.29)2+(5.5.29)2=(5.13.29)2
(20.5.13)2+(21.5.13)2=(5.13.29)2
És ez a módszer tetszőlegesen kiterjeszthető (mivel végtelen sok különböző pithagoraszi számhármas van), és mint látható, a jobb oldalakon mindig ugyanaz a szám áll.
|
| Előzmény: [173] Borgi - Tóth Áron, 2007-03-21 22:05:13 |
|
| [173] Borgi - Tóth Áron | 2007-03-21 22:05:13 |
 na, találtam egyet, ileltve hát kettőt 16 63, 65; 33 53, 65
ebböl arra merek következtetni hogy létezik sok ilyen pár, és létezik olyan x szám amihez n db, iylen pár tartozik.
|
|
| [172] Borgi - Tóth Áron | 2007-03-21 20:58:25 |
 sziasztok. remélem jó helyre írom a kérdésem.
lehet hogy a válasz már egyértelmű dolog, de én nem tudom, ezért bátorkodom megkérdezni
van-e olyan négyzetszám, ami több mint 1 négyzetszámösszeg párból előállitható?!
tehát
a2 + b2 = c2
és a,b,c egész számok. létezik-e olyan c, amihez több a és b pár tartozik?
|
|
| [171] fermel | 2007-03-17 20:27:28 |
 Ismét egy kombinatorikai feladat megoldásában szeretnék segítséget kérni. 13-as totóról van szó. Ebből 6 kimenetele egyértelmű, a további 7 pedig kétesélyes. Hány "szelvényt" kell legkevesebb kitölteni ahhoz, hogy biztosan legyen 12 találat? Adjuk is meg azokat a kitöltéseket, amelyek ezt biztosítják!
Odáig eljutottam, hogy 16 szelvény kitöltése elegendő. Viszont elképzelésem sincs arról, hogy milyen szisztéma szerint "töltsem ki a 16 szelvényt", hogy biztosan legyen 12 találat. (Végül is 7 kétesélyesből kell hatot biztosan eltalálni)
Köszönöm a segítséget: fermel
|
|
| [170] Lóczi Lajos | 2007-03-08 14:53:08 |
 Nézd meg pl. a Sárközy-Surányi: Számelméletfeladat-gyűjteményt, illetve annak függelékét. (Teljes bizonyításokat nem fogsz találni mindkettőre, de sok útmutatást igen.)
|
| Előzmény: [169] S.Ákos, 2007-03-07 20:14:06 |
|
| [169] S.Ákos | 2007-03-07 20:14:06 |
 Sziasztok!
Meg tudnáktok mondani, hogy hol lehet arra bizonyítást találni, hogy
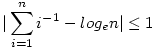
illetve

mindig mindig teljesül(pi az i-edik prímszám)?
|
|



 R2 függvények magasabbrendű deriváltjai multilineáris leképezések) sokszor használatosak.
R2 függvények magasabbrendű deriváltjai multilineáris leképezések) sokszor használatosak. 



