| [2189] marcius8 | 2018-10-23 14:57:32 |
 Az könnyen látható, hogy a \(\displaystyle q_1\) és \(\displaystyle q_2\) kvaterniókhoz létezik olyan \(\displaystyle q\) kvaternió, amelyre teljesül, hogy a \(\displaystyle q_1\) kavternió a \(\displaystyle q\) kvaterniónak valamilyen (egész) kitevőjű hatványa, és a \(\displaystyle q_2\) kvaternió a \(\displaystyle q\) kvaterniónak valamilyen (egész) kitevőjű hatványa, akkor \(\displaystyle q_1*q_2=q_2*q_1\) egyenlet teljesül. Igaz-e ennek az állításnak a megfordítása?
|
|
| [2188] marcius8 | 2018-07-21 16:55:42 |
 \(\displaystyle n\) darab egymással szabályos ötszöget feldarabolunk az átlói mentén. Így keletkezik \(\displaystyle 5n\) darab egyenlő szárú háromszög, melyeknek szögei 36°, 36°, 108°, keletkezik \(\displaystyle 5n\) darab egyenlő szárú háromszög, melyeknek szögei 72°, 72°, 36°, és keletkezik \(\displaystyle n\) darab kisebb, egymással egybevágó szabályos ötszög. Milyen \(\displaystyle n\) esetén rakható össze a keletkezett síkidomokból mindegyiket pontosan egyszer felhasználva egy nagyobb szabályos ötszög?
|
|
|
|
| [2185] marcius8 | 2018-07-02 10:55:54 |
 Végül is a primnégyzetek reciprokösszege csak egy másik végtelen összeggel lett felírva, amelynek értéke el lett nevezve. Ez nagyjából annak a beismerése, hogy igazából semmit sem tudunk erről az összegről. De a [2183] kérdés nagyon jó!!!! A [2184] válasz meg érdekes. A [2183] kérdés annyira tetszett nekem, hogy ezzel kapcsolatban nekem is eszembe jutottak a következő kérdések:
Mit tudunk a \(\displaystyle 4k+1\) alakú pozitív prímek reciprokösszegéről? Mit tudunk a \(\displaystyle 4k-1\) alakú pozitív prímek reciprokösszegéről?
Mit tudunk a \(\displaystyle 6k+1\) alakú pozitív prímek reciprokösszegéről? Mit tudunk a \(\displaystyle 6k-1\) alakú pozitív prímek reciprokösszegéről?
|
| Előzmény: [2184] Lóczi Lajos, 2018-07-01 09:45:07 |
|
|
| [2183] Bátki Zsolt | 2018-06-30 15:55:57 |
 Mint tudjuk a természetes számok reciprokának az összege végtelen (divergens a sor) A prímszámokra is végtelen: azaz sum (1/p) nagyon soknál is több. Sum (1/i*i) Négyzetszámok reciprok összege (pi*pi/6, Euler alapján) véges.
De mennyi sum (1/(p*p)) azaz:prímek négyzetének reciprok összege mennyi? nem találtam erre az interneten. Próbáltam számolni de nem sokra jutottam a sejtésben, hogy mennyi. Írok rá programot, de az nem hozza ki a formulát, ha van egyáltalán. Köszi a segítségetek. 1/(2*2)+1/(3*3)+1/(5*5)+1/(7*7)+1/(11*11)+1/(13*13)+1/(17*17) =0.439...
|
|
| [2182] Erben Péter | 2018-06-30 14:00:50 |
 Jobban átgondolva a hivatkozott elemibb megoldást, látok benne egy hiányosságot (abban az esetben, amikor a legkisebb háromszög valamelyik szélen van), és nem vagyok biztos benne, hogy ez (egyszerűen) javítható.
|
| Előzmény: [2181] Erben Péter, 2018-06-30 11:08:13 |
|
| [2181] Erben Péter | 2018-06-30 11:08:13 |
 Ha jól értem, háromszögekre először W. T. Tutte bizonyította, hogy nem lehetséges ilyen felbontást csinálni. (Dissections into Equilateral Triangles, in. The Mathematical Gardner (1981))
Itt van egy elemibb megoldás, ami analóg azzal, ahogy kockákra szokás bizonyítani a lehetetlenséget.
Legyen az \(\displaystyle ABC\) szabályos háromszög \(\displaystyle A\) csúcsát lefedő háromszög \(\displaystyle AXY\). Az \(\displaystyle XY\) oldalt különböző hosszú háromszög oldalak fedik, ezek közül a legrövidebb \(\displaystyle PQ\) (\(\displaystyle P\) vagy \(\displaystyle Q\) eshet az eredeti háromszög oldalára is), és a szabályos háromszög \(\displaystyle PQR\).
A \(\displaystyle P\) és \(\displaystyle Q\) csúcsú ,,felfelé álló'' háromszögek közül legalább az egyik kisebb, mint \(\displaystyle PQR\), különben ezek \(\displaystyle R\)-nél egymásba csúsznának.
Legyen mondjuk \(\displaystyle PKL\) a kisebb. Most a \(\displaystyle PKL\) háromszög átveszi \(\displaystyle AXY\) szerepét, és megint fogunk találni egy \(\displaystyle PKL\)-nél kisebb ,,felfelé álló'' szürke háromszöget a felbontásban.
Mivel a leírt logika tetszőlegesen sokáig folytatható, nem állhat véges sok háromszögből a felbontás.
|
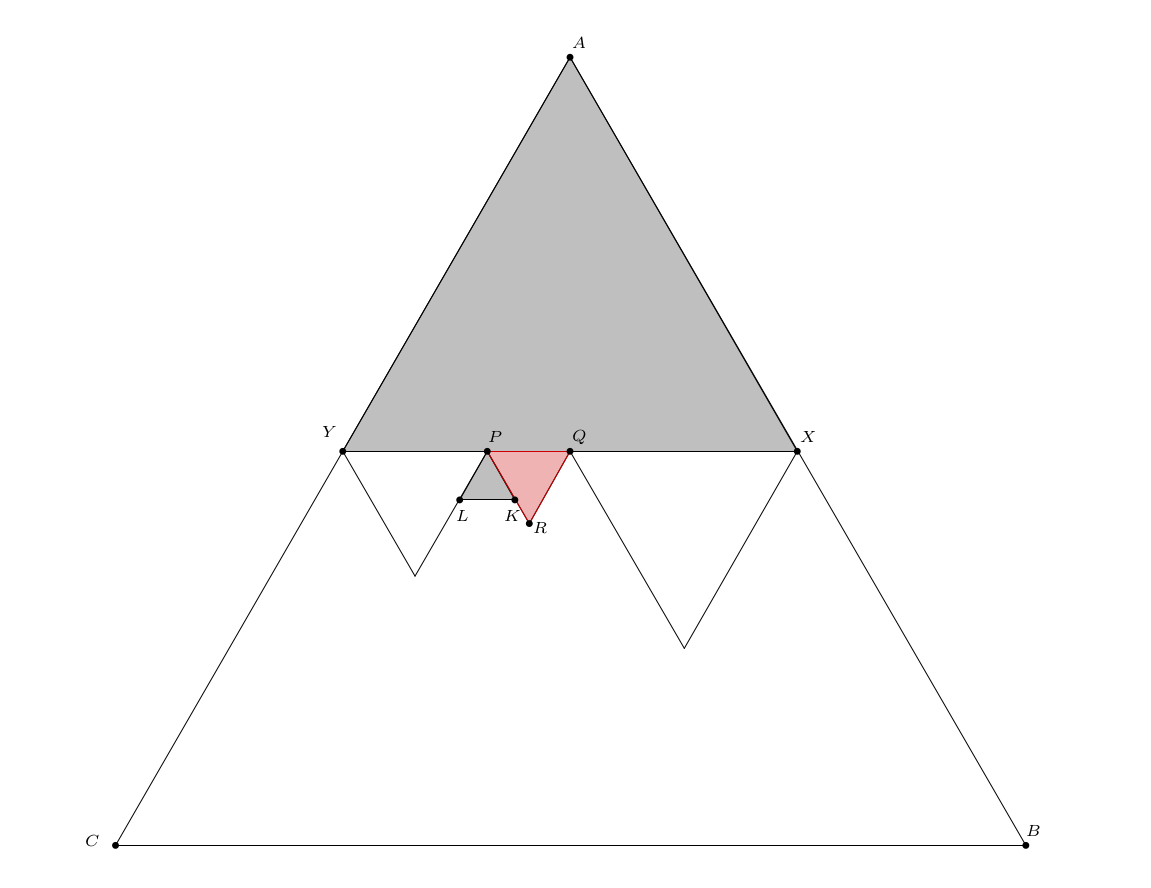 |
| Előzmény: [2180] marcius8, 2018-06-23 20:14:32 |
|
| [2180] marcius8 | 2018-06-23 20:14:32 |
 Arie Duijvestijn (remélem, jól írom a nevet) holland matematikus egy négyzetet felbontott különböző méretű négyzetekre. (Lásd: ábra). Vajon egy szabályos háromszöget is fel lehet bontani különböző méretű szabályos háromszögekre?
|
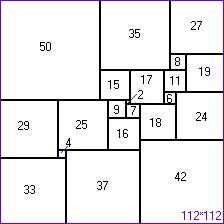 |
|







