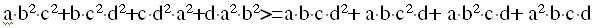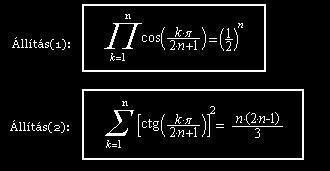| [264] nadorp | 2008-01-15 20:48:41 |
 Sajnos a "Szűcs rendezési tételt" nem olvastam, de gyanakszom, hogy a következőtől nem áll messze. Egyébként ezt anal gyakon vettük és úgy tudtam, hogy ez a Csebisev-egyenlőtlenség :-( pedig tényleg nem az.
Legyenek a1 a2 a2 ... ... an és b1 an és b1 b2 b2 ... ... bn nemnegatív számok. Ekkor, ha a {ci} számok a bi számok egy tetszőleges permutációja, akkor bn nemnegatív számok. Ekkor, ha a {ci} számok a bi számok egy tetszőleges permutációja, akkor
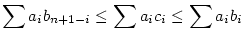 . .
Ha ezt felhasználjuk, akkor igaz az eredeti feladat következő általánosítása ( hacsak megint nem néztem el valahol egy egyszerűsítést :-)
Legyenek a1 a2 a2 ... ... an (n an (n 3) pozitív számok. Ekkor 3) pozitív számok. Ekkor
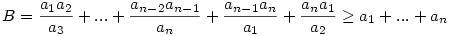
Kezdjük a végén az utolsó két taggal, ekkor
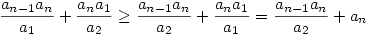 . Tehát . Tehát
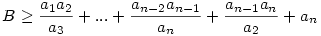
Újra a fenti "rendezési tételt" alkalmazva a két utolsó törtre
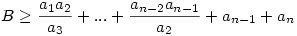
Ezt folytatva, előbb utóbb ezt kapjuk
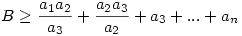
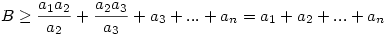
|
| Előzmény: [263] epsilon, 2008-01-15 15:20:39 |
|
| [263] epsilon | 2008-01-15 15:20:39 |
 Köszi sakkmath a javítást (örömömben észre sem vettem a végén az elírást), na meg kösz a szakreferenciát. Mivel nem jutok hozzá ahoz a forráshoz amit írtál, megfogalmaznád a Szűcs-tételt? Tisztelettel üdv: epsilon
|
|
|
|
| [260] epsilon | 2008-01-12 08:58:36 |
 Helló nadorp! A feladat 5 vagy több tag esetén is igaznak tűnik, de a 4-re adott bizonyítást sok eset letárgyalása nélkül nem igazán látom átültetni pl 5 tagra :-( Van valami ötleted? Üdv: epsilon
|
| Előzmény: [258] nadorp, 2008-01-08 11:29:29 |
|
| [259] epsilon | 2008-01-08 15:02:50 |
 Helló! Köszi, jó ötlet volt az, hogy azt az 1 törtet ami nem illett bele a Cebisev egyenlőtlenségbe (a rendezés monotonításába), 2 esetbe véve tárgyaltad, így valóban teljesen logikus, szép megoldás! Üdv: epsilon
|
|
| [258] nadorp | 2008-01-08 11:29:29 |
 Mindkét oldalt elosztva a nem 0 abcd-vel,a feladat ekvivalens a következővel:
 . .
Két esetet vizsgálunk meg
1.eset: bc ad. Ekkor a Csebisev egyenlőtlenség és ad. Ekkor a Csebisev egyenlőtlenség és 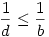 miatt miatt
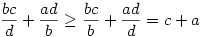
és hasolóan cd ab és ab és 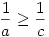 miatt miatt
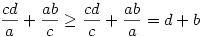
2.eset: bc>ad. Ekkor bc cd és cd és 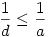 miatt miatt
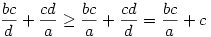
és hasolóan ad ab és ab és 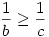 miatt miatt
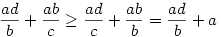
Összeadva a fenti két egyenlőtlenséget
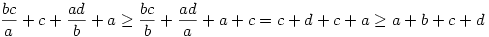
|
| Előzmény: [257] epsilon, 2008-01-07 13:40:07 |
|
| [257] epsilon | 2008-01-07 13:40:07 |
 B.Ú.É.K. Mindenkinek! Megint van egy szimpatiklus kis feladat, a Cebisev egyenlőtlenségre gyanakszom, de nem tudom a feltételeket hozzá igazítani: Ha a, b, c, d pozitív és növekvő számok ebben a sorrendben, akkor igaz a következő egenlőtlenség:
|
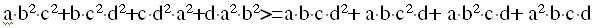 |
|
| [256] Róbert Gida | 2007-12-20 10:20:47 |
 D. O. Skljarszkij-N. N. Csencov-I. M. Jaglom Válogatott feladatok és tételek az elemi matematika köréből című könyvben ez 231.a feladata. Megoldás a könyv végén.
|
| Előzmény: [255] PAL, 2007-12-19 23:15:02 |
|
| [255] PAL | 2007-12-19 23:15:02 |
 Sziasztok! A segítségeteket szeretném kérni a (2)-es állítás bizonyításához. Az (1)-es egyenlőségre, mely a másodikhoz "külsőre" hasonló típusú, szép és "középiskolás fejjel" is könnyen érthető, 5-7 soros bizonyítási módszert találtam Pogáts Ferenc: Trigonometria(1973) c. könyvének 179. oldalán. Ezt azért írom le, mert hasonlóan frappáns bizonyítást keresek az állítás(2)-höz is. Tehát azonos algebrai átalakításokkal, lemmák alkalmazása nélkül, egy rövid, 5-6 soros bizonyítás lenne számomra praktikusan megfelelő (úgy tudom, hogy elvileg van ilyen, de nekem sajnos nem sikerült összehozni. Még talán a teljes-indukciós lenne a legjobb). Ha valaki tud ilyet - vagy bármilyet - hálás lennék érte, ha felrakná ide, vagy e-mailben elküldené nekem. Köszönöm.
|
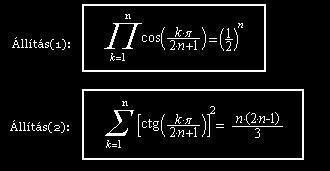 |
|



 a2
a2 3) pozitív számok. Ekkor
3) pozitív számok. Ekkor