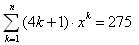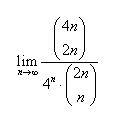|
|
| [376] epsilon | 2008-03-17 14:59:13 |
 Helló cauchy! "(277) Nekem az jön ki, hogy m = -2." Ez hogyan jött ki, mert Nekem az m×m-2m+3=0 egyenlet jött ki, így nincs megoldás :-( valóban így lenne? "(131) Nem azért, mert [0, 4) a helyes?" Ez valóban teéjesen Ok, mert nem föltétlen muszáj, hogy a nevező 2-od fokú legyen, lehet "degenerált" is, és akkor nem szükséges a d<0 mert az már értelmetlen. Kösz az észrevételt! Üdv: epsilon
|
| Előzmény: [365] cauchy, 2008-03-07 22:15:03 |
|
| [375] epsilon | 2008-03-17 14:45:58 |
 116-os: Minden n pozitív egész szám esetén jelölje Inv(n) azon (x,y) egész számpárok számát amelyek szimmetrizálhatók és amelyekre x×x+y×y=n×n. Mennyi a következő összeg értéke: Inv(1)+Inv(2)+Inv(3)+...+Inv(2005)
|
|
| [374] epsilon | 2008-03-17 14:41:38 |
 Közben még előkerültek a múlt héten függőben maradtak, íme még egy:245-ös. Tekintsük a lennebb látható egyenletet, minden n>=2 pozitív egészre. Melyek azok az n értékek, amelyekre az egyenletnek van legalább 1 pozitív egész megoldása? A válasz: 4s+3 ahol s nemnegatív egész, ellenben Én már n=3 esetén nem láttam az egész megoldást, hiszen ez a245=5×5×11 pozitív osztói közül való kell legyen. Nagyon gyanus ez az eredmény. Az lenne a kérdésem, hogy az n=4s+3 bár egy szükséges feltétel? Mert szerintem nem elégséges, vagy tévedek? Itt az egyenlet:
|
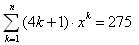 |
|
| [373] epsilon | 2008-03-17 14:28:05 |
 Helló! Ismét jelentkezem, egy jámbornak tűnő limesszel, hiába fejtettem ki a kombinációkat, egszerűsítés után sem találtam valami olyan alakra ami a megadot limeszértéket adja. (Ezt egyenlőre még nem mondanám meg, mert megint azt vadászom, vajon az eredmény jó-e?) Íme a limesz, és előre is kösz bármilyen jó tippet! Üdv: epsilon
|
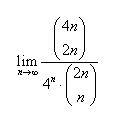 |
|
| [372] epsilon | 2008-03-09 19:24:31 |
 Talán a legrövidebb megoldás erre a feladatra az affixumokkal ( a csúcsokhoz rendelt komplex számokkal) van: Legyenek rendre a,b,c,d az ABCD négyszög csúcsainak affixumai, legyenek M,N,P,Q az AB, BC, CD, DA oldalak felezőpontok affixumai, ezért: m=1/2(a+b), n=1/2(b+c), p=1/2(c+d), q=1/2(d+a). Az MNPG paralelogramma <=> m+p=n+q ami azonnal adódik.
|
|
|
| [370] Róbert Gida | 2008-03-08 22:27:36 |
 Halálismert példa. Legyen ABCD a négyszög. P az AB oldal felezőpontja, Q az BC oldalé, R a CD oldalé, S a DA oldalé. Ekkor a felezőpontok által meghatározott négyszög csúcsai sorrendben: PQRS. Az, hogy paralellogramma azzal ekvivalens, hogy a szemközti oldalai párhuzamosak, azaz PQ||RS és QR||SP kell. De PQ az ABC háromszög középvonala, így párhuzamos az alappal, ami az AC, továbbá RS a CDA háromszög középvonala, így párhuzamos az alappal, ami az AC. Ergó mindkettő párhuzmaos az AC-vel, így PQ és RS egymással is párhuzamosak. Hasonlóan QR és SP is párhuzamos. Ami kellett.
Standard megoldása egyébként vektorokkal van. Az is elemi.
|
| Előzmény: [369] Onkie, 2008-03-08 22:12:28 |
|
| [369] Onkie | 2008-03-08 22:12:28 |
 Sziasztok!
Valaki el tudná küldeni e-mailben annak a tételnek a bizonyítását, hogy bármely tetszőleges négyszög oldalainak felezőpontjait összekötve paralelogrammát kapok? Az egész napomat a bizonyítással töltöttem, eredménytelenül... A segítséget előre is köszönöm! E-mail címem: xuli27@hotmail.com
U.i.: ha nem oldható meg az e-mailben való elküldés, e-mailben írd meg, hogy válaszoltál. Ez esetben is előre köszönöm a fáradozásokat!
|
|