| [425] leni536 | 2008-04-07 22:22:31 |
 A gyökvonásra való módszer nagyon tetszik, már el is sajátítottam a "digit by digit"-et. Más függvényekre van módszer a Taylor-soron kívül? Raj lenne papíron logaritmust számolni. Amúgy ha egy fügvénynek könnyebben számoljuk az inverz függvényét és inverz függvényének a deriváltját, a függvény mindenhol konvex, vagy mindenhol konkáv, akkor az alábbi sorozat határértéke tart a függvényünk értékéhez az x0 helyen:
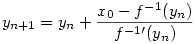
Ebből ki is jön n. gyökre a babilóniai módszer.
|
| Előzmény: [411] Sirpi, 2008-04-04 14:19:18 |
|
|
| [423] epsilon | 2008-04-07 19:41:32 |
 Helló! Megint van egy kedves feladat, látszatra jámbor:
|
 |
|
|
| [421] Sirpi | 2008-04-07 18:38:22 |
 Nem megy máshogy. A kettő teljesen ekvivalens: ha mondasz k-t és l-et, én megmondom x-et és y-t, és fordítva.
Ha nagy számokat akarsz felbontani, akkor amire rákereshetsz, mert sokkal jobban működnek, minthogy  -ig megnézünk minden prímet, hogy osztja-e n-t: -ig megnézünk minden prímet, hogy osztja-e n-t:
Pollard  -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk. -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.
|
| Előzmény: [418] csewe, 2008-04-07 14:59:55 |
|
|
| [418] csewe | 2008-04-07 14:59:55 |
 tulajdonképpen amint látom nekem n - et fel kel lbontanom "fejben/papiron" két szám szorzatára.
akkor viszont nem igen jutottam elöbre , mert ez nagyob számoknál már gondot okozhat. nincs más megoldás?
mert n felbontása csak találgatással megy.
|
| Előzmény: [420] Sirpi, 2008-04-07 13:42:32 |
|
| [420] Sirpi | 2008-04-07 13:42:32 |
 Oké, hogy csak páratlanra kell, de pl. a 10-et vagy a 42-t írd fel ilyen szorzat alakban, nem fog menni. Ahogy írtam, a 4-gyel oszthatók mennek, a csak 2-vel, de 4-gyel nem oszthatóak pedig nem.
Páratlanra meg úgy megy, ahogy írtam: n-et felbontod k.l-re, és innen 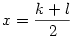 , ,  . .
Példa: n=91=7.13, ekkor 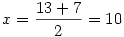 , , 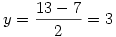 , és tényleg: 91=(10+3).(10-3) , és tényleg: 91=(10+3).(10-3)
|
| Előzmény: [417] csewe, 2008-04-07 12:50:16 |
|
| [417] csewe | 2008-04-07 12:50:16 |
 ismételten bocs
amire én használnám,ott
n mindíg páratlan pozitív egész
de nem értem miért nem lehet párosra felbontani hiszen
ha behejettesítem,akkor van olyan eset is
(6 + 2) * (6 - 2) = 32
de végül is ez mindegy mert nekem kimondottan páratlan
n - re kell a megoldás
a levezetést értem "azt hiszem", de még mindíg nem tudom
számszerüsíteni.
|
| Előzmény: [416] Sirpi, 2008-04-07 10:31:03 |
|
| [416] Sirpi | 2008-04-07 10:31:03 |
 Igazából az előző kérdésed után most nem vagyok egész biztos abban, hogy mire is vagy kíváncsi :-)
Ennek a feladatnak két része van, egy bazinehéz, meg egy könnyű. A bazinehéz az, hogy hogy bontsuk fel n-et két szám szorzatára (na jó, mondjuk tizensok jegytől tud ez már problémás lenni). Mivel x+y és x-y paritása azonos, ezért vagy mindkettő páros, vagy mindkettő páratlan. így n-et két azonos paritású szám szorzatára kell felbontani. Ha n páratlan, akkor nem is lehet máshogy, viszont ha n páros, akkor két páros szorzatára kell (egy 4k+2 alakú számot nem lehet így felbontani).
Ha ez megvan, vagyis n=k.l, ahol k l, akkor x+y=k, x-y=l, és innen triviálisan l, akkor x+y=k, x-y=l, és innen triviálisan 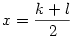 , ,  . .
|
| Előzmény: [415] csewe, 2008-04-07 05:35:20 |
|






 -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.
-módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk. l, akkor x+y=k, x-y=l, és innen triviálisan
l, akkor x+y=k, x-y=l, és innen triviálisan