Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] [212] [213] [214] [215] [216] [217] [218] [219] [220] [221] [222] [223] [224] [225] [226] [227] [228] [229] [230]

Szeretnél hozzászólni? Jelentkezz be.

[761] Tibixe

2009-01-30 16:26:18

Az analízissel szenvedjenek csak a fizikusok, az esetszétbontogatással meg a hentesek... Gyönyörűen kijön számelmélettel.

Vegyük mindkét oldal p alapú logaritmusát.

q^p=(log_p q) p^q

Tehát log_pq racionális, t/s alakban felírható, ahol t és s relatív prím egészek.

Innen

sq^p=tp^q

Ekkor lesz egy u pozitív egész szám, amire

p=u^t q=u^s

Visszahelyettesítve:

t u^{su^t}=s u^{tu^s}

Az általánosság megszorítása nélkül feltehetjük, hogy

su^t $\ge$ t^s

. Az előző egyenlet mindkét oldalát osztva:

t=s u^{tu^s-su^t}

Az előző feltétel miatt u^{tu^s-su^t} egész. Mivel t és s pozitív relatív prím egészek, u^{tu^s-su^t} csak 1 lehet. Tehát t=s. Az egyetlen önmagával rel. prím pozitív egész pedig az 1. Innen pedig

p=u¹=q

[760] nadorp

2009-01-30 08:09:03

Ha p=1 akkor q=1 és fordítva, tehát ezekben az esetekben igaz az állítás. Feltehető, hogy p,q $\geq$ 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz

q^p>p^q

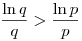
$\frac{\ln q}q>\frac{\ln p}p$

Mivel az 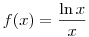$f(x)=\frac{\ln x}x$ függvény x $\geq$ e esetén szigorúan monoton csökken, ezért 3 $\leq$ p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor

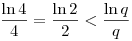$\frac{\ln4}4=\frac{\ln2}2<\frac{\ln q}q$ miatt szintén a monoton csökkenésből adódóan q<4,tehát csak q=3 lehet. Viszont a p=2 q=3 értékek esetén nem teljesül az eredeti egyenlőség. Azt kaptuk, p<q nem lehet. Teljesen hasonlóan adódik, hogy p>q sem lehetséges, tehát p=q

Előzmény: [759] Kiss Béla, 2009-01-29 20:53:36

[759] Kiss Béla

2009-01-29 20:53:36

Sziasztok! Sagítséget szeretnék kérni a következő feladathoz. Foggalmam sincs, hogy hogyan lehetne megoldani:

Bizonyítsuk be, hogyha a p és q pozitív egész számokra fenn áll a p^{q^p}=q^{p^q}, akkor p=q.

[757] BohnerGéza	2009-01-24 16:31:35
Ábra egy kis segítséggel. A párhuzamos helyzet esetén látszik HoA állítása.

Előzmény: [755] HoA, 2009-01-22 18:47:09

[756] Gyöngyő

2009-01-24 10:26:40

Sziasztok!

Lenne egy kérdésem!

Tudjuk,hogy 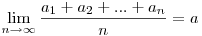$\lim_{n \rightarrow \infty}\frac{a_1+a_2+...+a_n}{n}=a$

bizonyítsuk be,hogy

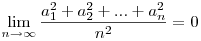
$\lim_{n \rightarrow \infty}\frac{a^2_1+a^2_2+...+a^2_n}{n^2}=0$

ahol a_i pozitív valós számok.

Üdv.: Gyöngyő

[755] HoA	2009-01-22 18:47:09
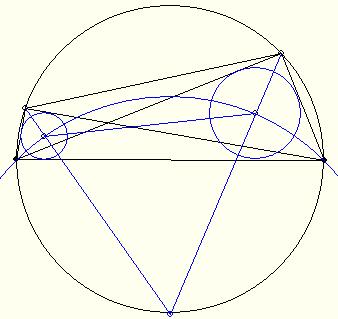
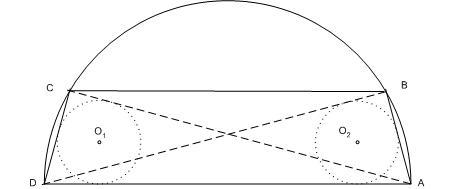
Ott viszont nem reagált rá senki. Idemásolom, hogy ne kelljen lapozgatni: Az ABCD konvex négyszögben AD=2. Az ABD szög és az ACD szög derékszög. Az ABD háromszög szögfelezőinek metszéspontja gyök(2) távolságra van az ACD háromszög szögfelezőinek a metszéspontjától. Mekkora a BC oldal hossza? Az ugye világos, hogy az adatok nem egyértelműen határozzák meg ABCD négyszöget. Kérdés, hogy BC hossza egyértelmű-e. 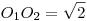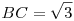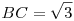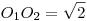Szimmetrikus esetben ABCD egyenlőszárú trapéz és elég könnyen kiszámolható, hogy ha $O_1 O_2 = \sqrt{2}$ , akkor $BC = \sqrt{3}$ Feladatok: - adjunk geometriai bizonyítást a szimmetrikus esetre - adjunk bizonyítást az általános esetre - igaz-e a tétel fordítottja: Ha $BC = \sqrt{3}$ , akkor $O_1 O_2 = \sqrt{2}$ ?

Előzmény: [754] sakkmath, 2009-01-22 10:42:23

[754] sakkmath	2009-01-22 10:42:23
Érdekes matekfeladatok [2813], klikk ide.
Előzmény: [753] Valezius, 2009-01-21 20:22:43

[753] Valezius

2009-01-21 20:22:43

Láttam valamelyik topikban egy feladatot, de most az istenért se találom, valaki nem tudja, melyikben van?

ABCD konvex négyszög, ABD és ACD derékszög. Ugyanezekbe, mint háromszögbe írt körök középpontjai gyök(2) távolságra vannak.

Csak érdekelne, hogy jól emlékszem-e rá.

[752] j.milan	2009-01-17 21:55:07
Közben javítanám saját magam, más irányban kijött a megoldás :) üdv
Előzmény: [751] j.milan, 2009-01-17 21:22:57

[751] j.milan	2009-01-17 21:22:57
Jóestét! Az én kérdésem az, hogy mi azon pontok mértani helye a síkon, amelyek három ponttól vett távolságának négyzetösszege állandó.
Előzmény: [750] Gyöngyő, 2009-01-17 16:31:28

Már regisztráltál?
Új vendég vagy?