| [827] HoA | 2009-02-24 14:08:59 |
 Köszönöm Káli gúla szép megoldását. Azt hiszem, segít még jobban rávilágítani arra, mi a bajom ezzel a feladattal. Fussunk tehát neki harmadszor is, ezúttal az ő jelöléseit is használva:
Egy egyenletes v1 sebességgel haladó, M méter hosszú menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott t mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont M métert tesz meg. A kérdés, mekkora utat tett meg a futár összesen? ( Számadatok: t = 15 s , M = 1000 m )
A futár megtett útja [822] megoldóképlete szerint így alakul:
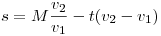 | (1) |
Mint az várható volt, a megtett út a feladatban szereplő M,t,v1ésv2 mennyiségektől függ. M és t konkrét értéke adott, de v1ésv2 szerepét jótékony homály fedi. Gondolhatnánk, hogy azok is az M és t ismeretében értelmes határok között szabadon megadhatók, csak most éppen nem rendelünk hozzájuk számértéket. De ez nem így van. A feladat túlhatározott, adott M és t mellett már v1ésv2 nem választható meg egymástól függetlenül. Az adatok közötti megkötést éppen [822] feltételi egyenlete adja:
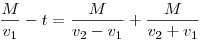 | (2) |
Ha M,v1ésv2 értéke lenne adott, megtehetnénk, hogy (2) –ből kifejezzük t-t és ezt behelyettesítjük (1) –be. Rövid átalakítások után [824] szép képletét kapjuk:
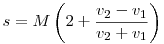 | (3) |
De az ekkor sem lenne igaz, hogy „akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát”, hiszen egy adott M,v1ésv2 hármashoz egy konkrét, éppen a (2) egyenletből adódó t érték tartozik.
Nekünk azonban Mést adott. Mit tehetünk, hogy bemenő adatainktől egyértelműen függő eredményt kapjunk? Az egyik megoldás laci777 „izzadási iránya”: (2) –ből v2-re másodfokú egyenletet kapunk. Ennek fizikailag értelmes gyökét választva v2 -nek ezt a kifejezését behelyettesítjük (1) –be és kapunk egy csúnya , de csak M-et,t-tésv1-et tartalmazó kifejezést. A másik megoldás az, hogy elfogadjuk (3) szép képletét megoldásnak, de hozzátesszük, hogy „ahol v1 szabadon választott sebesség a 0<v1<M/t tartományban, v2 pedig a (2) feltételből számított M,t,ésv1 által meghatározott sebesség”. És ekkor persze a (3) képletben szereplő mennyiségekhez éppen a megadott t érték trtozik.
|
| Előzmény: [824] Káli gúla, 2009-02-23 19:14:32 |
|
| [826] tudniakarok | 2009-02-24 13:46:11 |
 Sziasztok! Kérlek segítsetek!
Az a problémám, hogyha adott tetszőleges db nemnegatív szám, akkor hogyan tudnám elrendezni őket egy mátrixba úgy hogy a lehető legegyenletesebb elrendezést kapjam.(Arra gondolván, hogy a két legnagyobb szám a "legtávolabb" legyen egymástól, és így tovább...) Van-e erre vmilyen már kidolgozott algoritmus, mert nem nagyon találom a szakirodalmakban!? Van ötletem, de elég egyszerűnek találom ráadásul nagy számításigényű,hátha vki tud jobbat!
Előre is köszi a segítséget!
|
|
| [825] laci777 | 2009-02-23 23:22:06 |
 Kedves Káli Gúla!
Köszönöm szépen ezt a megoldást is, bár őszintén szólva olyat igyekeztem volna kiizzadni (a jelzett eredménnyel:(), ahol a menetoszlop (a példa adatai szerint 0<v1<240 km/h közt értelmezhető) sebessége az egyedüli független változó, ahogyan valóban is annak a függvénye minden egyéb tényező (a v2 és az egyes szakaszok s és t értékei egyaránt). Még egyszer köszönöm.
|
| Előzmény: [824] Káli gúla, 2009-02-23 19:14:32 |
|
| [824] Káli gúla | 2009-02-23 19:14:32 |
 Működik az is. Legyen v2=kv1, a menetoszlop hossza M. Amíg fel- és lefut, addig 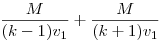 idő telik el, ez alatt a menet idő telik el, ez alatt a menet 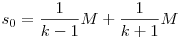 , a futár pedig , a futár pedig 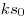 utat tesz meg. A középső időszakban együtt mennek, ez a feltétel miatt utat tesz meg. A középső időszakban együtt mennek, ez a feltétel miatt 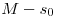 , tehát a futár összesen , tehát a futár összesen 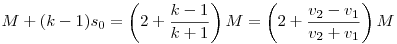 utat tett meg a feladat adataival (akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát vagy ha 0 mp-et ment volna). utat tett meg a feladat adataival (akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát vagy ha 0 mp-et ment volna).
|
| Előzmény: [823] laci777, 2009-02-23 16:53:01 |
|
| [823] laci777 | 2009-02-23 16:53:01 |
 Kedves HoA!
Köszönet (ismét) a segítségért. Úgy gondoltam eredetileg, hogy az egyes időintervallumokban megtett utakkal operálok, de boncolás (+eltévedés:() lett sajna belőle...
Még egyszer köszönöm szépen.
|
| Előzmény: [822] HoA, 2009-02-23 10:08:45 |
|
| [822] HoA | 2009-02-23 10:08:45 |
 Szerintem a feladatban nem az okozza a gondot, hogy „a megoldáshoz vezető másodfokú egyenlet túl kemény dió” , hanem az, hogy a feladat egy kicsit tisztességtelenül van kitűzve. Az egyik szokásos középiskolai feladattípus szövegében megadnak bizonyos paramétereket és az eredményt ezek függvényében várják. Ha zárójelben megadják a paraméterek numerikus értékét is, akkor ezeket az eredmény képletébe behelyettesítve számszerű eredményt is tudunk adni . Másik fekadattípus az, ahol egy fizikai jelenség kapcsán bizonyos mennyiségek közötti összefüggések keresése, értékhatárok megállapítása a cél. Itt a kettő keveredik, a baj csak az, hogy ez a szövegből nem derül ki egyértelműen. Tisztességesnek valahogy így érezném a feladat kitűzését:
Egy egyenletes v1 sebességgel haladó menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott 15 mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont 1 km-t tesz meg. A kérdés, mekkora utat tett meg a futár összesen? Milyen összefüggés áll fenn v1 és v2 között, ha tudjuk, hogy a menetoszlop 1 km hosszú?
Megoldás: A futár teljes menetideje 1000/v1 mp, ebből 15 mp-ig v1, egyébként v2 sebességgel haladt, a megtett út tehát s =  méter. A v1ésv2 közötti összefüggést abból állapítjuk meg, hogy a futár 1000/v1-15 mp alatt az 1000 méteres oszlop végéről az elejére majd vissza ment, menetideje tehát: méter. A v1ésv2 közötti összefüggést abból állapítjuk meg, hogy a futár 1000/v1-15 mp alatt az 1000 méteres oszlop végéről az elejére majd vissza ment, menetideje tehát: 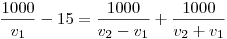 Ezek után a v2-re adódó másodfokú egyenletet elemezhetjük, milyen v1 értékekre kapunk pozitív v2-t, v2 milyen határok között változhat, stb. Végül v2-t v1 függvényeként felírva behelyettesíthetjük a megtett út képletébe, így az egy csak v1 -től függő kifejezés lesz, de továbbra sem egy konkrét számérték. Ezek után a v2-re adódó másodfokú egyenletet elemezhetjük, milyen v1 értékekre kapunk pozitív v2-t, v2 milyen határok között változhat, stb. Végül v2-t v1 függvényeként felírva behelyettesíthetjük a megtett út képletébe, így az egy csak v1 -től függő kifejezés lesz, de továbbra sem egy konkrét számérték.
|
| Előzmény: [815] laci777, 2009-02-22 00:21:36 |
|
| [821] Lóczi Lajos | 2009-02-22 18:20:58 |
 Rögzített x H-ra n H-ra n  esetén fn(x) esetén fn(x) f(x):= f(x):= x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy  . Ezt kell igazolni most. Ehhez egy kis függvényvizsgálatra van szükség. . Ezt kell igazolni most. Ehhez egy kis függvényvizsgálatra van szükség.
1. Látszik, hogy ha x rögzített, akkor a konvergencia n-ben monoton: fn(x)<fn+1(x)<f(x), vagyis |fn(x)-f(x)|=f(x)-fn(x)=:gn(x).
2. Pl. L'Hospital-lal belátod, hogy  illetve két deriválással, hogy gn(x) konkáv. De gn(0)=0 is igaz. Vagyis rögzített n-re gn olyan nemnegatív konkáv függvény, amely 0-ban 0, a végtelenben pedig a határértéke pozitív. Egy ilyen függvény viszont minden x illetve két deriválással, hogy gn(x) konkáv. De gn(0)=0 is igaz. Vagyis rögzített n-re gn olyan nemnegatív konkáv függvény, amely 0-ban 0, a végtelenben pedig a határértéke pozitív. Egy ilyen függvény viszont minden x H esetén kisebb, mint a limesze, tehát H esetén kisebb, mint a limesze, tehát 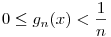 , minden x-re és n-re. , minden x-re és n-re.
3. Emiatt 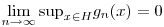 . .
|
| Előzmény: [819] plac, 2009-02-22 14:22:15 |
|
| [820] Lóczi Lajos | 2009-02-22 17:23:04 |
 Viszont igazzá válik az állítás, ha megköveteljük, hogy a két végpontban ugyanazok legyenek a függvényértékek, vagyis f(a)=g(a) és f(b)=g(b) legyen.
Ekkor ugyanis a két konvex alakzat tartalmazni fogja egymást (az egyik alakzat a két végpont, az őket összekötő szakasz és f "lelógó" grafikonja által határolt síkidom; a másik ugyanígy, csak g-vel), és ismert (itt a Fórumon már kétszer is előkerült a bizonyítása, csak meg kell keresd :), hogy ha egy konvex alakzat tartalmaz egy másikat, akkor a külső alakzat kerülete nem lehet kisebb.
|
| Előzmény: [818] M. Feri, 2009-02-22 13:45:13 |
|
| [819] plac | 2009-02-22 14:22:15 |
 Hello! A kérdésem a következő lenne. Valaki megtudja nekem mondani, hogy fn(x)=x.arctan(nx), H=(0, ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni. ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni.
|
|
|






 H-ra n
H-ra n
 esetén fn(x)
esetén fn(x) x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy
x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy