| [860] gubanc | 2009-03-13 12:41:36 |
 Nagyrabecsült FÓRUMOSOK! Sehogy sem bírok ezzel a feladattalÿ:( segítenétek?
Legyenek n és k adott pozitív egészek és tekintsük azon f: {1; 2; 3; ...; n}  {-k; -k+1; ...; k-1; k} függvényeket, amelyekre |f(i) - f(j)| {-k; -k+1; ...; k-1; k} függvényeket, amelyekre |f(i) - f(j)| k bármely i, j k bármely i, j {1; 2; 3; ...; n} esetén. Hány ilyen f függvény van? {1; 2; 3; ...; n} esetén. Hány ilyen f függvény van?
Üdv: gubanc
|
|
|
|
| [857] Lóczi Lajos | 2009-03-08 20:49:07 |
 Itt minden bizonnyal két dolgot érdemes összekombinálni: van egy képlet az integrálfüggvény Fourier-együtthatóinak kiszámítására (az eredeti függvény Fourier-együtthatóiból), így elég csak a logaritmus és a kotangens függvény kompozíciójának meghatározni a sorfejtését. (A függvény paritása miatt az egyik paritású együtthatók nullák lesznek.) A kotangenset szétbontva, lényegében ln (cos ).sin , ln (cos ).cos , ln (sin ).cos , ln (sin ).sin integrandusú határozott integrálok maradnak (az argumentumokban persze a megfelelő helyeken ott a szumma futóindexe). Ezeket az integrálokat ki lehet számolni (persze az integrandus nem korlátos volta miatt az integrálok konvergenciáját ellenőrizni kell), egyszer kiszámítottam őket, de csak elég trükkösen jöttek ki. (Utólag aztán látható volt, hogy az a feladat a 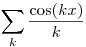 és és  függvénysorok összegével van kapcsolatban, amelyeket egyszerűbben egy függvénysorok összegével van kapcsolatban, amelyeket egyszerűbben egy 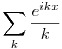 komplex exponenciális sor összegeként volt érdemes kiszámolni.) Szóval esetleg próbálj meg ezeket a nyomokon elindulni; mindenesetre a direkt számolások nem lesznek egyszerűek. komplex exponenciális sor összegeként volt érdemes kiszámolni.) Szóval esetleg próbálj meg ezeket a nyomokon elindulni; mindenesetre a direkt számolások nem lesznek egyszerűek.
|
| Előzmény: [855] plac, 2009-03-07 16:12:53 |
|
| [856] Lóczi Lajos | 2009-03-08 20:00:58 |
 Ha a diszkrimináns kisebb nullánál, a képlet formálisan ugyanaz, csak konjugált komplex számokat tartalmaz (amelyek együttesen valós értéket adnak). De az Euler-összefüggésekkel ezt az esetet mindig átírhatod exponenciális függvényt és szinuszt/koszinuszt tartalmazó alakra, amiben már csak valós számok vannak.
|
| Előzmény: [854] akinom91, 2009-03-07 13:03:18 |
|
|
| [854] akinom91 | 2009-03-07 13:03:18 |
 Köszönöm szépen mind a két megoldási módot, sikerült az explicit képletet is megkapni (igaz, segítséggel, még életemben ilyet nem csináltam). A lényeg, hogy mind a 2 hasznos volt, tanultam valami újat, csak máskor is fel tudjam magamtól is használni. Ha már itt tartunk valaki fel tudná nekem írni, hogy a Fibonacci-féle sorozatot, hogy kell megadni explicit módon? Ezt kaptam:
Fibonacci sorozat: apn+1=bpn+cpn-1
Karakterisztikus egyenlet: aR2=bR+c; R1, R2 a karakterisztikus egyenlet megoldásai.
Ha R1=R2 => pn=R1n(A+nB); Ha R1 R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!) R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!)
Ott akadtam meg, ha a karakt. egyenlet esetében  <0. Ilyen esetben, hogy lehet felírni az explicit képletet? <0. Ilyen esetben, hogy lehet felírni az explicit képletet?
Előre is köszi!
|
| Előzmény: [853] Káli gúla, 2009-03-07 00:54:41 |
|
| [853] Káli gúla | 2009-03-07 00:54:41 |
 Ha E-vel jelölöd a csupa egyesekből álló mátrixot, akkor A=E-I, tehát A2+A=(E2-2E+I)+(E-I)=E2-E, ami a csupa kettesekből álló mátrix, ezért A2+A=2E=2(A+I). Ez ugyanaz, mint az a), és ebből A-val szorzással, indukcióval adódik a c) is.
|
| Előzmény: [852] akinom91, 2009-03-06 23:19:33 |
|
| [852] akinom91 | 2009-03-06 23:19:33 |
 Hát sajnos az első megoldásodnál fogalmam sincs, miről beszélsz, a másodikat meg nagyjából értem, amennyit leírtál (én is valami képletet próbáltam keresni). Meglátjuk, sikerül-e explicit képletet találni, ugyanis még ilyet nem oldottam, és nem tudom mennyire lehet gimnáziumi szinten... . És akkor a képletet amit feltételezzük, hogy megkapok, kell még bizonyítani mat. ind. módszerével, vagy ez már megvolt? :D Köszi a tippet az elinduláshoz, remélem érettségiig már kívülről fújom a típusfeladatok megoldásainak módszerét. :)
|
| Előzmény: [851] jonas, 2009-03-06 22:50:12 |
|
| [851] jonas | 2009-03-06 22:50:12 |
 A (c) pontot többféleképp is meg lehet közelíteni. Az egyik lehetőség, hogy az A mátrixot Jordan blokk alakra hozod, és ezt hatványozod.
A másik, hogy felhasználod az (a) pontot, amely szerint A2=A+2I ami alapján A3=A(A2)= A(A+2I)=A2+2A=3A+2I. Ebből megsejted, hogy az általános hatvány felírható An=pnA+qnI alakban. Valóban: An+1=A.An= A(pnA+qnI)=pnA2+qnA= (pn+qn)A+2pnI. Ebből pn+1=pn+qn, és qn=2pn, amiből pn+1=pn+2pn-1. A kezdeti feltétel is nyilván teljesül: p0=0,q0=1, p1=1,q1=0. (Persze ellenőrizned kell, hogy nem számoltam el.) Ennek a rekurziónak megkeresheted az explicit képletét. (Ez elvileg nem, csak gyakorlatban egyszerűbb annál, mintha az An mátrix mind a kilenc elemére írnál föl együttes lineáris rekurziót.)
|
| Előzmény: [850] akinom91, 2009-03-06 22:33:50 |
|



 {-k; -k+1; ...; k-1; k} függvényeket, amelyekre |f(i) - f(j)|
{-k; -k+1; ...; k-1; k} függvényeket, amelyekre |f(i) - f(j)| k bármely i, j
k bármely i, j {1; 2; 3; ...; n} esetén. Hány ilyen f függvény van?
{1; 2; 3; ...; n} esetén. Hány ilyen f függvény van? 


 ,
, R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!)
R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!)  <0. Ilyen esetben, hogy lehet felírni az explicit képletet?
<0. Ilyen esetben, hogy lehet felírni az explicit képletet? 
