|
|
| [1056] torcsi2010 | 2010-02-11 19:25:21 |
 és hogy mi látható ezen a képen és hogy mire használjuk ? előre is köszönöm
|
 |
|
| [1055] torcsi2010 | 2010-02-11 19:24:24 |
 halli valaki megtudja nekem mondani hogy miért csináljuk ezt a fizikai kísérletet ? /szappanoldatba mártott drótváz/
|
 |
|
| [1054] Fernando | 2010-02-09 10:58:46 |
 Szia Attila!
Először nekem is ennél lényegesebb nagyobb valszín jött ki (kb. tízszerese), de rájöttem, hogy ott rosszul alkalmaztam a De-Morgan azonosságot. Másodjára kétféleképpen kijött ugyanaz, mint mzperx-nek! Ha itt ezt szabad megbeszélni, akkor megbeszélhetnénk a megoldásokat, kinek hogyan jött ki.
|
| Előzmény: [1053] jenei.attila, 2010-02-05 11:27:02 |
|
| [1053] jenei.attila | 2010-02-05 11:27:02 |
 A val.-et jól számoltad. A téglatest felszíne pedig kisebb egyenlő mint a testátló négyzetének kétszerese, itt 648 (kockára teljesül). A teljesen elfajuló "téglatest felszíne pedig 0.Vagyis valóban nem elég az adat.
|
| Előzmény: [1052] mzperx, 2010-02-04 22:16:14 |
|
| [1052] mzperx | 2010-02-04 22:16:14 |
 Sziasztok, van két feladatom, az egyikben nem vagyok biztos, hogy jól oldottam meg, a másik meg szerintem igy nem elég.Légyszi segitsetek. 1. Magyarországon az autókat olyan rendszámtáblával látják el, melyen 3 betű és 3 számjegy szerepel( a betűkhöz az ABC 25 betűjét használják). Véletlenszerűen kiválasztva egy rendszámtáblát, mekkora annak a valószinűsége, hogy a betűk is és a számjegyek között is vannak egyformák? Szerintem 0, 032704. 2. Egy téglatest középpontja a testátló egyik harmadoló pontjától 3 cm távolságra van. mekkora a téglatest felszine? Szerintem túl kevés igy az adat.
|
|
| [1051] Fernando | 2010-02-03 22:46:48 |
 A kérdés elején nem úgy érted, hogy legyen F elemi felület R3- ban? Nem ígérem, hogy tudok érdemben válaszolni, egyelőre csak egy masszív fejfájásig jutottam el.. :) Node azért elővettem a saját ábrákkal bővített diffgeo könyvet...
|
| Előzmény: [1049] TiCoN314, 2010-01-09 13:23:19 |
|
| [1050] Fernando | 2010-02-03 13:04:09 |
 Kedves Cokee!
A tétel bizonyítása megtalálható: Dr. Leindler László Analízis című könyvében. Fellapozva a 76-77-dik oldalakat visszautal a Professzor a 49-dik oldalon olvasható 5.2.3 tételre, aminek aránylag hosszú a bizonyítása, az 51-dik oldal közepéig tart.
|
|
| [1049] TiCoN314 | 2010-01-09 13:23:19 |
 Üdv!
Differenciálgeometriával kapcsolatban lenne 1 kérdésem :)
Szóval adott egy 3 dimenziós felület r paraméterezéssel, G pedig 1 felületi görbe. (G(t) = r(g(t)), ahol g(t)=(g1(t),g2(t)) síkgörbe). Ekkor G deriváltja, G'(t) érintővektormező lesz a felületen. Ha G'(t)-t, mint a felületen értelmezett éritővektormezőt lederiváljuk a G görbe t pontban vett eritővektor irányában, akkor ez miért lesz egyenlőt G''(t)-vel, vagyis a G görbe t pontban vett 2. deriváltjával? Remélem érthető volt. :)
Válaszokat előre is köszönöm!
TiCoN
|
|
| [1048] Cokee | 2009-12-29 21:41:59 |
 Sziasztok!
Azt szeretném megkérdezni,hogy hol tudom megtalálni a bizonyítását a következőnek:
Függvények határértéke(véges hé. véges helyen),a két definíció ekvivalenciája(Cauchy-Heine)
Köszönöm előre is. Üdv.: Cokee
|
|
|
| [1045] jenei.attila | 2009-12-26 10:53:25 |
 Sőt, a sin 0-beli deriváltjára sem szerencsés hivatkozni, mert az éppen a nevezetes határérték, tehát logikai körforgás alakul ki. Na de nem is ez a lényeg, ezt tekintsétek inkább szőrszálhasogatásnak. Boldog Karácsonyt mindenkinek!
|
| Előzmény: [1044] jenei.attila, 2009-12-26 10:47:54 |
|
| [1044] jenei.attila | 2009-12-26 10:47:54 |
 Egy kis elírás: x nem 0-hoz, hanem végtelenbe tart. Alma! Szerintem nem szerencsés a L'Hospital szabályra hivatkozni, mivel ahhoz a sin fv.-t tudni kell deriválni. Azonban a szóban forgó határérték (sin(x)/x x->0) nevezetes, amelynek ismerete kell a sin deriválásához.
|
| Előzmény: [1046] Sirpi, 2009-12-25 23:37:01 |
|
|
| [1046] Sirpi | 2009-12-25 23:37:01 |
 Így van, ahogy mondod.
![\lim_{x \to \infty} \left[ x\cdot \sin(n/x)\right] = \lim_{x \to \infty} \frac {\sin(n/x)}{1/x} = n \cdot \lim_{x \to \infty} \frac {\sin(n/x)}{n/x} = n\cdot 1 = n](keplet.cgi?k=D30D402D7A257FEF)
Utóbbinál felhasználtuk, hogy a szinusz fv. meredeksége a 0-ban 1, azaz sin '0=1 (a 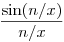 hányados a (0;0) és az (n/x;sin(n/x) pontokat összekötő szakasz meredeksége, ez 1-hez tart, ha n/x tart a 0-hoz. Ugyanez van a tangens függvény esetén is. hányados a (0;0) és az (n/x;sin(n/x) pontokat összekötő szakasz meredeksége, ez 1-hez tart, ha n/x tart a 0-hoz. Ugyanez van a tangens függvény esetén is.
|
| Előzmény: [1042] Hosszejni Darjus, 2009-12-25 22:33:40 |
|
| [1042] Hosszejni Darjus | 2009-12-25 22:33:40 |
 sziasztok! számológéppel szoktam próbálkozni magyarórán, hogy érdekes dolgokat találjak, és azt vettem észre (pontosabban arra következtetek az eredmények alapján), hogy ha x tart a végtelenbe és n egy valós szám, akkor
lim(x*tan(n/x))=lim(x*sin(n/x))=n.
Tudnátok erről mondani vmit (hogy hogyan lehetne bizonyítani, vagy hogy ez hülyeség, stb.)?
előre is köszi
|
|
|
| [1040] Yvi | 2009-12-15 22:41:36 |
 Köszönöm! Lenne még egy feladat, amivel nem boldogulok, íme: határozza meg az alábbi függvény lokális szélsőérték helyeit és esetleges nyeregpontjait: F(x,y,)=ex3+y2+12xy ahol x3+y2+12xy az e kitevői és x a köbön, y a négyzeten van. (még nem nagyon megy a képletszerkesztő használata)
|
| Előzmény: [1039] kallosbela, 2009-12-15 21:36:13 |
|
|
| [1038] Yvi | 2009-12-15 21:04:41 |
 Sziasztok, van egy kérdésem hogyan deriváljuk 4/xy-t parciálisan xre ha az egy rendes tört? kell a 4-et is deriválni? köszi előre is!
|
|
|
|
| [1035] Higgs | 2009-12-10 23:30:15 |
 Üdv!
Létezik olyan képlet amivel a 2 négyzetszám összegeként felírható számok számát 0, és n között meg lehet határozni?
|
|
|












