Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91]

Szeretnél hozzászólni? Jelentkezz be.

[1085] Marika	2010-03-12 20:04:59
Sziasztok! Ebben is segítségre szorulok. Egy háromszög két oldala 6,5cm és 7,3cm a közbezárt szög 72fok. Egy másik háromszög egyik oldala 13,4 a rajta fekvő 2 szög 30fok és 78fok. Egybevágó-e a két háromszög? köszönöm ha segittek megoldani .!

[1084] Marika	2010-03-12 19:48:09
Sziasztok! Szeretnék segítséget kérni! Megmagyarázná valaki hogy kell ezt a feladatot meg csinálni? Hegyes szögű-e az a háromszög melyben a szokásos jelölésekkel? A=17cm B=11cm C=22cm Előre is köszönöm a segítséget!

[1083] Janosov Milán

2010-03-11 00:33:50

Köszönöm a segítséget, és/de közben sikerült megoldanom a problémát (numerikus integrálással).

És esetleg azt lehet tudni, miért lassult be ma este a munkafüzet olyannyira, hogy esetenként tízszer kellett frissíteni, mire történt valami? Határidőkor ez kicsit tragikus :(

Előzmény: [1082] Alma, 2010-03-09 20:52:53

[1082] Alma	2010-03-09 20:52:53
Mit szeretnél kiszámolni? Hátha tudunk segíteni.
Előzmény: [1081] Janosov Milán, 2010-03-09 12:49:09

[1081] Janosov Milán	2010-03-09 12:49:09
Köszönöm a javaslatokat, az integrálás mint olyan azt hiszem már nem probléma. A függvényeimet kell egyszerűsíteni (kisebb függvényekre szépen dolgozik), az eredmént - már ha ad egyáltalán - nem szép, és nem is használható :).
Előzmény: [1080] Lóczi Lajos, 2010-03-09 11:55:49

[1080] Lóczi Lajos	2010-03-09 11:55:49
Arra vigyázz, hogy a program először y szerint, aztán x szerint integrál, ha Integrate[...,{x,...},{y,...}]-t írsz.
Előzmény: [1075] Janosov Milán, 2010-03-08 15:27:14

[1079] dfkuu

2010-03-08 21:07:08

Sziasztok! Sürgős lenne! A De Morgan azonosságot kellen bizonyítanom, de nem Venn-diagram segítségével, sajnos azt nem fogadták el.

Valaki mondja meg!

[1078] Alma	2010-03-08 18:34:29
Igen. Nekem az az általános tapasztalatom, hogy az Integrate parancs sokkal lassabb, ha határozott integrált számoltatsz ki, mintha primitív függvényét kérnéd csak. Így, én vagy határozatlanul integráltatok, vagy az NIntegrate paranccsal numerikusan számoltatok.
Előzmény: [1077] Janosov Milán, 2010-03-08 17:24:05

[1077] Janosov Milán	2010-03-08 17:24:05
Köszönöm, működik a szintaxis! Az létezhet, hogy kicsit bonyolultabb (törtkitevők, négy változó) függvénynél (tíz)perceket számol?
Előzmény: [1076] Alma, 2010-03-08 15:44:53

[1076] Alma

2010-03-08 15:44:53

próbáld a következőt ki:

$f\left[x\_,y\_\right]:=x^2+y^2;$

Integrate[f[x,y],{x,0,1},{y,0,1}]

Elvileg ennek így működnie kell, az eredmény 2/3. Próbáld először ezt, majd saját problémádon a szintaxist.

Előzmény: [1075] Janosov Milán, 2010-03-08 15:27:14

[1075] Janosov Milán

2010-03-08 15:27:14

Üdv!

A kérdésem valaki olyanhoz szól, aki jártas a Mathematica (7.0.1) kezelésében. Többváltozós függvényt szeretnék integrálni (több változó szerint), de sajnos nem sikerül (a 0-tól 1-ig vett határozott integrálban is lesz változó). Az alábbi szintaxis szerint próbáltam: Integrate[f(x1,x2,x3,...),(x1,0,1),(x2,0,1),...(xn,0,1)] - sima zárójelek helyett persze kapcsossal. Ha valaki tudna adni egy jó példát, hálás lennék!

[1074] BohnerGéza	2010-03-07 17:10:43
Célszerű jelölni a számjegyet, ha nem írható le mind egy karakterrel: pl. (5)(15), vagy (5)(1)(5) mást jelent. Ezt oldják meg a 16-os szr-ben az A=10, B=11, ..., F=15 jelöléssel.
Előzmény: [1072] D. Tamás, 2010-03-06 20:29:04

[1073] AzO	2010-03-06 21:13:07
A feladatot ugyan nem ismerem, de pont az indokolja, hogy 515 az utolso ket szamjegy, amit magad is irtal: 5^.17+15^.1=100, azaz az utolso helyiertekre a 15 kerul, az utolso elottire az 5. Jelolhetnenk betukkel is a 17-es szamrendszer szamjegyeit, es akkor minden egyes helyiertekre egykarakteres szimbolum kerulhetne, mint ahogy az a 10-es szamrendszerben megszokott.
Előzmény: [1072] D. Tamás, 2010-03-06 20:29:04

[1072] D. Tamás	2010-03-06 20:29:04
A B.4251-es feladat megoldása közben felmerült bennem egy kérdés: mit értünk egy adott p alapú számrendszer utolsó két számjegyén? Namost, ha p kisebb, mint 11, akkor egyértelmű, de a p nagyobb mint 10 akkor például a 100 a 17-es számrendszerben 515, hiszen 517+151=100. Éppen emiatt merültek fel nekem gondok, hogy most a 15 az utolsó két számjegy, vagy az 515?

[1070] S.Ákos	2010-02-27 12:37:38
BC+BD+BE>BC+DE=BC+AC>AB=2. 2 háromszög-egyenlőtlenség az ABC és BDE háromszögekre, meg kellett ugye AC=DE.
Előzmény: [1069] m.atekoos, 2010-02-27 11:24:09

[1069] m.atekoos

2010-02-27 11:24:09

Tudnátok segíteni?

Itt a feladat: egy egységnyi sugarú kör kerületére felvesszük ilyen sorrendben: A C D E B úgy hogy AB átmérő, tehát C,D,E egy félköríven helyezkedik el. Tudjuk hogy AC=DE. Biz be hogy CB+DB+EB>=2.

[1068] torcsi2010	2010-02-15 19:53:05
köszi a segítséget és sajnálom hogy a második kép nem jött össze :(

[1067] Fernando

2010-02-14 10:30:47

Valóban, helyesen:

$P(AB)=1-P(\overline{AB})=1-P(\overline{A}+\overline{B})=1-P(\overline{A})-P(\overline{B})+P(\overline{A}*\overline{B})$

Előzmény: [1066] jenei.attila, 2010-02-14 10:00:35

[1066] jenei.attila	2010-02-14 10:00:35
A képletsorod végén $P(\overline{AB})$ helyett $P(\overline{A}*\overline{B})$ lenne helyesen, amúgy a számolás jó. Számomra az én megoldásom egyszerűbbnek és jobban általánosíthatónak tűnik, persze ez ízlés dolga.
Előzmény: [1065] Fernando, 2010-02-13 13:36:05

[1065] Fernando

2010-02-13 13:36:05

Harmadik megoldás. Legyen A az az esemény, hogy a betűk között van egyezés. B , hogy a számok között van. Ekkor a De Morgan azonosságból a Poincaré formulával:

$P(AB)=1-P(\overline{AB})=1-P(\overline{A}+\overline{B})=1-P(\overline{A})-P(\overline{B})+P(\overline{A}\overline{B})$

$=1-\frac{25*24*23*10^3+25^3*10*9*8-25*24*23*10*9*8}{25^3*10^3}=0,032704$

Előzmény: [1064] Fernando, 2010-02-13 13:16:19

[1064] Fernando

2010-02-13 13:16:19

Összes eset ok, ismétléses variációk számának szorzata. Az én gonolatmenetem: kedvezők: tekintsük a betűket: a pár helyét 3-féleképpen tudjuk kiválasztani, a párok száma 25*24 és ehhez hozzáadjuk azokat az eseteket, amikor mindhárom betű azonos -tehát25-öt- hiszen nekünk az is jó. A számoknál ugyanígy járunk el. És kapcsolat van, szorzunk. Kapjuk:

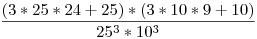
$\frac{(3*25*24+25)*(3*10*9+10)}{25^3*10^3}$

Ez amúgy egyenlő azzal amit te írtál és mzperx-nek is ez jött ki számszerint, a keresett valszín:

0,032704

Előzmény: [1063] jenei.attila, 2010-02-13 11:48:03

[1063] jenei.attila

2010-02-13 11:48:03

Az összes lehetséges rendszám 25³*10³. A páronként különböző betűket tartalmazó betűhármasok száma: 25*24*23, amiből a legalább két egyforma betűt tartalmazó betűhármasok száma : 25³-25*24*23. Hasonlóan a legalább két egyforma számjegyet tartalmazó számhármasok száma: 10³-10*9*8. A két kifejezés szorzata megadja a betűkben, és a számokban is legalább két egyforma jegyet tartalmazó rendszámok számát. Vagyis a keresett val.-ég:

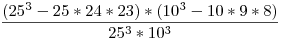
$\frac{(25^3-25*24*23)*(10^3-10*9*8)}{25^3*10^3}$

Előzmény: [1054] Fernando, 2010-02-09 10:58:46

[1062] Fernando	2010-02-12 19:00:33
A kép alapján akármi is lehet.
Előzmény: [1061] psbalint, 2010-02-12 16:06:53

[1061] psbalint	2010-02-12 16:06:53
Szerintem félreérted; ezt nem Leia használta, hanem Luke Skywalker! :)

[1059] Fernando	2010-02-12 11:24:09
Emlékeim szerint különösen jól sikerül a kísérlet, ha az oldathoz glicerint is adsz. A második képen látható eszköz "azonosíthatatlannak" tűnik. :(
Előzmény: [1055] torcsi2010, 2010-02-11 19:24:24

Már regisztráltál?
Új vendég vagy?