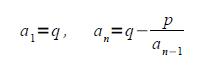|
| [1097] bily71 | 2010-03-27 21:34:26 |
 Üdv! Lenne egy kérdésem.
A törtek egészrészével fáradtságos munka a számolás, de azért vannak szabályok, amelyek megkönnyíthetik a dolgunkat, mint pl.: ![[x]-\left[\frac{x}{p}\right]=\left[\frac{(x-1)(p-1)}{p}\right]](keplet.cgi?k=CA0F15F193BE85D0) , vagy pl.: , vagy pl.: ![p\left[\frac{x}{p}\right]=[x-b]](keplet.cgi?k=B87A2531CDD0FC10) , ha a , ha a x<a+1, ahol a x<a+1, ahol a b (mod p), stb., (x b (mod p), stb., (x R, a,b R, a,b N, p N, p P). P).
Nem találtam megfelelő irodalmat, hol lehet bővebben olvasni erről a témáról?
|
|
|
|
| [1093] Sirpi | 2010-03-16 11:07:03 |
 Ugye a lánctört határértékben adja ki az értékét, és ha periodikus, akkor az általános trükk az, hogy ezt a határértéket elnevezzük A-nak, és megpróbálunk A-ra felírni egy egyenletet. Mivel 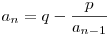 , ezért határértékben: , ezért határértékben:  , vagyis A2-Aq+p=0, és ezt már csak meg kell oldani A-ra, ami egy sima másodfokú egyenlet. , vagyis A2-Aq+p=0, és ezt már csak meg kell oldani A-ra, ami egy sima másodfokú egyenlet.
Persze az még kérdés, hogy a 2 gyök közül melyikhez fog tartani a lánctört...
|
| Előzmény: [1092] farkasroka, 2010-03-15 18:49:37 |
|
| [1092] farkasroka | 2010-03-15 18:49:37 |
 Sziasztok!
A következő sorozathoz keresnék képletet, ill. még arra lennék kíváncsi, hogy hogyan lehet egy általános lánctörtet átírni egyszerűre?
Segítségeteket előre is köszönöm!
|
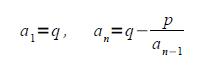 |
|
|
| [1090] Fernando | 2010-03-14 23:46:43 |
 A wolfram-ba beírva: zeta(1) ok; zeta(2) ok; zeta(-1)=-1/12. Miért is?
|
|
| [1089] Marika | 2010-03-13 16:01:18 |
 Nagyon szépen köszönöm a gyors segítséget!
|
|
|
| [1087] HoA | 2010-03-12 21:32:32 |
 A szögek alapján még nem lenne kizárt ( 30 + 78 + 72 = 180 ) , de az egybevágósághoz az kéne, hogy az oldalhosszak is megegyezzenek. Az pedig "ránézésre" is látszik, hogy 72 fokos szöget közbezáró 6,5 és 7,3 cm-es oldalak mellett a harmadik oldal nem lehet 13,4 cm ( alig kisebb, mint a két másik összege, 13,8 ) . Pontos válasz a cosinus tétel alapján: teljesül-e, hogy 13,42=6,52+7,32-2*6,5*7,3*cos72o . Szerintem nem, de számold ki.
|
| Előzmény: [1085] Marika, 2010-03-12 20:04:59 |
|
| [1086] Radián | 2010-03-12 21:26:04 |
 1084-re: Legyenek egy háromszög oldalai a,b,c, ahol a<=b<=c, ekkor a hegyesszögű háromszög oldalaira az alábbi feltétel teljesül: a*a+b*b>c*c ,ha a háromszög derékszögű: a*a+b*b=c*c (Pitagorasz-tétel),ha a háromszög tompaszögű: a*a+b*b<c*c (Ezek gyakorlatilag a koszinusztételből következnek.)
1085-re: Lehet egybevágó is, ha mindkét háromszög oldalainak hossza 6,5;7,3 és 13,4 cm , a szögek pedig a megfelelő módon 72,30,78 fokosak(13,4 cm-es oldalon fekvő 2 szög 30fok és 78fok, a vele szemközti pedig 72)hisz 72+30+78=180. Másképp nem lesz a két háromszög egybevágó.
|
| Előzmény: [1085] Marika, 2010-03-12 20:04:59 |
|
| [1085] Marika | 2010-03-12 20:04:59 |
 Sziasztok! Ebben is segítségre szorulok. Egy háromszög két oldala 6,5cm és 7,3cm a közbezárt szög 72fok. Egy másik háromszög egyik oldala 13,4 a rajta fekvő 2 szög 30fok és 78fok. Egybevágó-e a két háromszög? köszönöm ha segittek megoldani .!
|
|
| [1084] Marika | 2010-03-12 19:48:09 |
 Sziasztok! Szeretnék segítséget kérni! Megmagyarázná valaki hogy kell ezt a feladatot meg csinálni? Hegyes szögű-e az a háromszög melyben a szokásos jelölésekkel? A=17cm B=11cm C=22cm Előre is köszönöm a segítséget!
|
|
| [1083] Janosov Milán | 2010-03-11 00:33:50 |
 Köszönöm a segítséget, és/de közben sikerült megoldanom a problémát (numerikus integrálással).
És esetleg azt lehet tudni, miért lassult be ma este a munkafüzet olyannyira, hogy esetenként tízszer kellett frissíteni, mire történt valami? Határidőkor ez kicsit tragikus :(
|
| Előzmény: [1082] Alma, 2010-03-09 20:52:53 |
|
|
| [1081] Janosov Milán | 2010-03-09 12:49:09 |
 Köszönöm a javaslatokat, az integrálás mint olyan azt hiszem már nem probléma. A függvényeimet kell egyszerűsíteni (kisebb függvényekre szépen dolgozik), az eredmént - már ha ad egyáltalán - nem szép, és nem is használható :).
|
| Előzmény: [1080] Lóczi Lajos, 2010-03-09 11:55:49 |
|
|
| [1079] dfkuu | 2010-03-08 21:07:08 |
 Sziasztok! Sürgős lenne! A De Morgan azonosságot kellen bizonyítanom, de nem Venn-diagram segítségével, sajnos azt nem fogadták el.
Valaki mondja meg!
|
|
| [1078] Alma | 2010-03-08 18:34:29 |
 Igen. Nekem az az általános tapasztalatom, hogy az Integrate parancs sokkal lassabb, ha határozott integrált számoltatsz ki, mintha primitív függvényét kérnéd csak. Így, én vagy határozatlanul integráltatok, vagy az NIntegrate paranccsal numerikusan számoltatok.
|
| Előzmény: [1077] Janosov Milán, 2010-03-08 17:24:05 |
|
|
| [1076] Alma | 2010-03-08 15:44:53 |
 próbáld a következőt ki:
![f\left[x\_,y\_\right]:=x^2+y^2;](keplet.cgi?k=5495DBE406CD6BD3)
Integrate[f[x,y],{x,0,1},{y,0,1}]
Elvileg ennek így működnie kell, az eredmény 2/3. Próbáld először ezt, majd saját problémádon a szintaxist.
|
| Előzmény: [1075] Janosov Milán, 2010-03-08 15:27:14 |
|
| [1075] Janosov Milán | 2010-03-08 15:27:14 |
 Üdv!
A kérdésem valaki olyanhoz szól, aki jártas a Mathematica (7.0.1) kezelésében. Többváltozós függvényt szeretnék integrálni (több változó szerint), de sajnos nem sikerül (a 0-tól 1-ig vett határozott integrálban is lesz változó). Az alábbi szintaxis szerint próbáltam: Integrate[f(x1,x2,x3,...),(x1,0,1),(x2,0,1),...(xn,0,1)] - sima zárójelek helyett persze kapcsossal. Ha valaki tudna adni egy jó példát, hálás lennék!
|
|
| [1074] BohnerGéza | 2010-03-07 17:10:43 |
 Célszerű jelölni a számjegyet, ha nem írható le mind egy karakterrel: pl. (5)(15), vagy (5)(1)(5) mást jelent. Ezt oldják meg a 16-os szr-ben az A=10, B=11, ..., F=15 jelöléssel.
|
| Előzmény: [1072] D. Tamás, 2010-03-06 20:29:04 |
|
| [1073] AzO | 2010-03-06 21:13:07 |
 A feladatot ugyan nem ismerem, de pont az indokolja, hogy 515 az utolso ket szamjegy, amit magad is irtal: 5.17+15.1=100, azaz az utolso helyiertekre a 15 kerul, az utolso elottire az 5. Jelolhetnenk betukkel is a 17-es szamrendszer szamjegyeit, es akkor minden egyes helyiertekre egykarakteres szimbolum kerulhetne, mint ahogy az a 10-es szamrendszerben megszokott.
|
| Előzmény: [1072] D. Tamás, 2010-03-06 20:29:04 |
|



 x<a+1, ahol a
x<a+1, ahol a b (mod p), stb., (x
b (mod p), stb., (x R, a,b
R, a,b
 x2, akkor
x2, akkor