Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[1108] nadorp	2010-04-07 11:08:02
Annyiban igazad van, hogy hallgatólagosan kihasználtuk, hogy egy polinom minden pontjában folytonos, tehát hogy az $f(z)=\frac{z^n-1}{z-1}$ függvény a z=1 pontban folytonossá tehető, tehát minden z-re f(z)=z^n-1+...+z+1. Más szavakkal, z $\neq$ 1 esetén f(z)=z^n-1+...+z+1, de mivel a jobb oldal mindenhol folytonos, ezért f(1) a jobb oldal z=1 helyettesítési értékével értelmezhető
Előzmény: [1107] HoA, 2010-04-07 08:53:11

[1107] HoA

2010-04-07 08:53:11

A Geometria [1404] –ben kitűzött feladat szerepel Reiman István „Geometria és határterületei” és „Fejezetek az elemi geometriából” könyveiben. A megoldás ötlete az, hogy a komplex síkon az n-ik egységgyököket feleltessük meg a szabályos n-szög csúcsainak. Ezek az e_i egységgyökök a zⁿ=1 egyenlet megoldásai, a P=zⁿ-1=0 polinom nullhelyei, ahol e₀=1. Ezért a polinom felírható P=(z–1)(z–e₁)...(z–e_n-1) alakban. Ugyanakkor zⁿ-1=(z–1)(z^n-1+z^n-2+...+z+1) Mindkét kifejezést z-1 tényezővel osztva az adódó kifejezések z=1 helyen vett abszolútértékére adódik, hogy |(1–e₁)|^.|(1–e₂)|...|(1–e_n-1)|=1+1+..+1=n és itt a baloldal éppen a z=1 csúcsból a többi csúcsba húzott átlók hosszának szorzata.

A kérdés: „Középiskolában tanultuk”, hogy egy ilyen z-1 -gyel történő egyszerűsítés után a továbbiakban ki kell kötnünk, hogy z $\ne$ 1 . Itt pedig a folytatásban éppen a z=1 helyen nézzük a dolgokat. Nem hiányzik itt valami?

[1105] K Robi	2010-04-03 21:27:24
Köszönöm a gyors választ! És Lajosnak is.
Előzmény: [1104] sakkmath, 2010-04-03 21:21:18

[1104] sakkmath

2010-04-03 21:21:18

Ez a link így nem jön be, de így hívható be még: a Google-ba írd: köbszámok összege.

Kattints a harmadik találatra.

Előzmény: [1106] sakkmath, 2010-04-03 21:16:19

[1106] sakkmath

2010-04-03 21:16:19

Klikkelj ide. Itt az is kiderül, hogy a jobb oldalon már te is egyszerűsíthettél volna ... .

Megszerelve (kimaradt a http:// ...) Sirpi

Előzmény: [1102] K Robi, 2010-04-03 19:41:56

[1103] Lóczi Lajos	2010-04-03 21:11:48
Teljes indukcióval ki fog jönni. (Erre a kifejezésre keress rá.)
Előzmény: [1102] K Robi, 2010-04-03 19:41:56

[1102] K Robi

2010-04-03 19:41:56

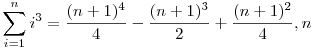$\sum_{i=1}^ni^3=\frac{(n+1)^4}{4}-\frac{(n+1)^3}{2}+\frac{(n+1)^2}{4},n$ természetes szám.

Meg tudná valaki mutatni a bizonyítását? Természetesen egy link is tökéletesen megfelelő olyan helyre, ahol megtalálom (lehetőleg magyar vagy angol vagy német nyelven).

[1101] Maga Péter	2010-03-29 08:52:14
A bizonyítás ,,helyből'' valóban nem könnyű. Van azonban egy valós függvénytani elmélet, aminek ez az egyik első alkalmazása. Lényegében azt lehet bebizonyítani, hogy egy valós-valós függvény folytonossági pontjainak halmaza előáll megszámlálható sok nyílt halmaz metszeteként (ez egyszerű következménye a folytonosság definíciójának); a racionális számok halmaza pedig nem (ez pedig következik Baire kategóriatételéből).
Előzmény: [1100] jonas, 2010-03-28 13:30:57

[1100] jonas	2010-03-28 13:30:57
Állítólag nincs, de ezt nem könnyű bizonyítani.
Előzmény: [1099] Hölder, 2010-03-28 13:18:20

[1099] Hölder	2010-03-28 13:18:20
Sziasztok! Arra lennék kiváncsi, hogy van -e olyan függvény, ami bármely valós szám esetén értelmezve van és a racionális pontokban folytonos, az irracionális pontokban pedig nem az?(pont a Riemann -féle függvénynek az "ellentettje")

[1098] bily71	2010-03-28 09:40:18
Bocs, még a kérdést is elírom:) ilyenekre gondoltam, mint pl.: $[x]-\left[\frac{x}{p}\right]=\left[\frac{(x+1)(p-1)}{p}\right]$ .
Előzmény: [1097] bily71, 2010-03-27 21:34:26

[1097] bily71

2010-03-27 21:34:26

Üdv! Lenne egy kérdésem.

A törtek egészrészével fáradtságos munka a számolás, de azért vannak szabályok, amelyek megkönnyíthetik a dolgunkat, mint pl.: $[x]-\left[\frac{x}{p}\right]=\left[\frac{(x-1)(p-1)}{p}\right]$ , vagy pl.: $p\left[\frac{x}{p}\right]=[x-b]$ , ha a $\le$ x<a+1, ahol a $\equiv$ b (mod p), stb., (x $\in$ R, a,b $\in$ N, p $\in$ P).

Nem találtam megfelelő irodalmat, hol lehet bővebben olvasni erről a témáról?

[1095] farkasroka	2010-03-16 13:03:10
Köszönöm a segítséget!

[1094] nadorp

2010-03-16 11:28:33

Legyenek x₁ és x₂ az x²-qx+p=0 egyenlet - akár komplex - gyökei. Ha x₁ $\neq$ x₂, akkor

$a_n=\frac{\left({x_2}^n-{x_1}^n\right)q-\left({x_2}^{n-1}-{x_1}^{n-1}\right)p}{\left({x_2}^{n-1}-{x_1}^{n-1}\right)q-\left({x_2}^{n-2}-{x_1}^{n-2}\right)p}$

Ha x₁=x₂, azaz q²=4p, akkor

$a_n=\frac{n+1}{2n}q$

Előzmény: [1092] farkasroka, 2010-03-15 18:49:37

[1093] Sirpi

2010-03-16 11:07:03

Ugye a lánctört határértékben adja ki az értékét, és ha periodikus, akkor az általános trükk az, hogy ezt a határértéket elnevezzük A-nak, és megpróbálunk A-ra felírni egy egyenletet. Mivel 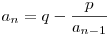$a_n=q - \frac p {a_{n-1}}$ , ezért határértékben: $A = q - \frac p A$ , vagyis A²-Aq+p=0, és ezt már csak meg kell oldani A-ra, ami egy sima másodfokú egyenlet.

Persze az még kérdés, hogy a 2 gyök közül melyikhez fog tartani a lánctört...

Előzmény: [1092] farkasroka, 2010-03-15 18:49:37

[1092] farkasroka

2010-03-15 18:49:37

Sziasztok!

A következő sorozathoz keresnék képletet, ill. még arra lennék kíváncsi, hogy hogyan lehet egy általános lánctörtet átírni egyszerűre?

Segítségeteket előre is köszönöm!

[1091] Lóczi Lajos	2010-03-15 03:00:16
"Mert" a Re(z)>1-re érvényes definiáló szummás alak analitikus kiterjesztéséből ez jön ki.
Előzmény: [1090] Fernando, 2010-03-14 23:46:43

[1090] Fernando	2010-03-14 23:46:43
A wolfram-ba beírva: zeta(1) ok; zeta(2) ok; zeta(-1)=-1/12. Miért is?

[1089] Marika	2010-03-13 16:01:18
Nagyon szépen köszönöm a gyors segítséget!

[1088] Radián	2010-03-13 09:26:33
Valóban, elnézést kérek tegnapi hanyagságomért.
Előzmény: [1087] HoA, 2010-03-12 21:32:32

[1087] HoA	2010-03-12 21:32:32
A szögek alapján még nem lenne kizárt ( 30 + 78 + 72 = 180 ) , de az egybevágósághoz az kéne, hogy az oldalhosszak is megegyezzenek. Az pedig "ránézésre" is látszik, hogy 72 fokos szöget közbezáró 6,5 és 7,3 cm-es oldalak mellett a harmadik oldal nem lehet 13,4 cm ( alig kisebb, mint a két másik összege, 13,8 ) . Pontos válasz a cosinus tétel alapján: teljesül-e, hogy 13,4²=6,5²+7,3²-26,57,3*cos72^o . Szerintem nem, de számold ki.
Előzmény: [1085] Marika, 2010-03-12 20:04:59

[1086] Radián

2010-03-12 21:26:04

1084-re: Legyenek egy háromszög oldalai a,b,c, ahol a<=b<=c, ekkor a hegyesszögű háromszög oldalaira az alábbi feltétel teljesül: a*a+b*b>c*c ,ha a háromszög derékszögű: a*a+b*b=c*c (Pitagorasz-tétel),ha a háromszög tompaszögű: a*a+b*b<c*c (Ezek gyakorlatilag a koszinusztételből következnek.)

1085-re: Lehet egybevágó is, ha mindkét háromszög oldalainak hossza 6,5;7,3 és 13,4 cm , a szögek pedig a megfelelő módon 72,30,78 fokosak(13,4 cm-es oldalon fekvő 2 szög 30fok és 78fok, a vele szemközti pedig 72)hisz 72+30+78=180. Másképp nem lesz a két háromszög egybevágó.

Előzmény: [1085] Marika, 2010-03-12 20:04:59

[1085] Marika	2010-03-12 20:04:59
Sziasztok! Ebben is segítségre szorulok. Egy háromszög két oldala 6,5cm és 7,3cm a közbezárt szög 72fok. Egy másik háromszög egyik oldala 13,4 a rajta fekvő 2 szög 30fok és 78fok. Egybevágó-e a két háromszög? köszönöm ha segittek megoldani .!

[1084] Marika	2010-03-12 19:48:09
Sziasztok! Szeretnék segítséget kérni! Megmagyarázná valaki hogy kell ezt a feladatot meg csinálni? Hegyes szögű-e az a háromszög melyben a szokásos jelölésekkel? A=17cm B=11cm C=22cm Előre is köszönöm a segítséget!

[1083] Janosov Milán

2010-03-11 00:33:50

Köszönöm a segítséget, és/de közben sikerült megoldanom a problémát (numerikus integrálással).

És esetleg azt lehet tudni, miért lassult be ma este a munkafüzet olyannyira, hogy esetenként tízszer kellett frissíteni, mire történt valami? Határidőkor ez kicsit tragikus :(

Előzmény: [1082] Alma, 2010-03-09 20:52:53

Már regisztráltál?
Új vendég vagy?