Fórum: Valaki mondja meg!

Pl. lineáris interpolációval: egy egyenesnek adott két pontban (30 és 40) az értéke, ebből felírod az egyenletét és megnézed, mit ad 37-nél.

"Van három feladatom"

Kihagytad a házi szót, nem?

Már régóta gondolom, hogy kellene a fórumon egy hf kérő topik.

Sziasztok! Van három feladatom, amivel kapcsolatban megkérdeznélek titeket, mi a véleményetek, mi a helyes megoldás? 1. Van olyan lineáris egyenletrendszer, amelynek végtelen sok megoldása van, de minden megoldása csak egész számokat tartalmaz. Úgy gondolom, hogy van, pl. x+y=0, ha x és y egészek, de nem tudom, hogy ilyenkor vehető -e az alaphalmaz tetszőlegesen. 2.Ha egy vektortérnek van nullvektortól különböző eleme, akkor végtelen sok eleme van. Úgy gondolom, jhogy igen, mert akkor a v vektor, mely nem nullavektor, annak tetszőleges pozitiv egész számszorosa is benne a van a vektortérben, de felmerült bennem az, hogy egy vektortér lehet -e igy véges, pl. -1, 0, 1 elemekből áll. 3. ha egy lineáris egyenletrendszer megoldásakor az elemi bázistanszformációk során egy ilyen sort találunk: x(2), 0, 1 , akkor nincs megoldás. Szerintem van, méghozzá az x(2) =1 -nek kell lennie.

Hali! Statisztikát is vágjátok?:) A kérdésem a következö lenne. Ha mondjuk a szabadság fok n-1=37 ezt hogy tudodm kikeresni táblázatbol?Akár khi-eloszlás, student eloszlás, F-eloszlás. Mert a táblázatban a szabadságfokok ugy vannak megadva hogy a 37 pont nincs megadva:)) 29 30 40 60 120 De akár monhatom azt is hogy 41 a szabadság fok mert, ez sincs benne:) Ilyenkor hogy kell kikeresni?

Köszi!

Egyébként pedig az OEIS A001235 sorozatában nézd meg a referenciákat, ha irodalmat akarsz kutatni.

Elég neked olyan szám, amit legalább kétféleképp lehet két köbszám összegeként fölírni? Mert akkor 1729^.n³ ilyen (n pozitív egész szám).

Legyen p_i annak a valószínűsége, hogy az i-edik mezőre lépünk a játék során (p₀=1), ekkor a teljes valószínűség tételéből: , itt minden p_i pozitív és triviálisan p₁₀₀>p₁₀₁>^...>p₁₀₅, ami kellett. Egyébként az is megmutatható, hogy nagy n-re (a játék véget ér, ha n-nél nagyobb egyenlő mezőre lépünk): , ha nin+5

Üdv!

Tegnap hallottam, hogy az 1729 a legkisebb szám, mely kétféleképpen írható fel 2 köbszám összegeként. Végtelen sok ilyen szám van? Van képlet mely csak ilyen számokat ad?

Gondolom a megoldás menete magában foglalja annak pontos bizonyítását is, hogy létezik ilyen legvalószínűbb érték!

Nem tűnik triviálisnak.

Engem is érdekel a "halálismert" megoldás menete!

A második kérdésre elfogadhatónak tartom (éjjel, 3/4 kettőkor) a következő gondolatmenetet:

Mivel elég sok dobás kell a 95-100 összeg eléréséhez, az ezek elérésének valószínűsége közti eltérés elhanyagolható a folytatáshoz képest. ...! ???

ja, ez pont elég, köszönöm szépen!

Szia! Ez talán jó lesz.

Sziasztok! . Tudna valaki adni egy linket ahol az összes csoport fel van sorolva modjuk 20-ad rendig vagy valami ilyesmi . Előre is köszönöm!

Talán nem mindenkinek halálismert (nekem egyáltalán nem volt az).

Másfelől viszont az én értelmezésemben az "átlépi" = "meghaladja", amiért is szerintem a 100 nem elfogadható megoldás.

Harmadrészt - és legfőképpen - : mi a megoldás módja, már akár az "eléri", akár a "meghaladja" értelmében? Engem érdekelne.

Másodikra 100 a megoldás, halálismert.

Sziasztok!

Tudna vki segíteni a következő feladatoknál:

Milyen vastag pénzérme esetén 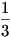a valószínűsége, hogy az érme az élére esik?

Szabályos dobókockával addig dobunk, míg a dobott számok S összege át nem lépi a 100-at. Mi S legvalószínűbb értéke?

Köszönettel:

Cokee

Üdv!

Holnap reggelre a következő feladatot tudnom kéne.Kerékpártömlőt pumpálunk. Szeretnénk elérni, hogy 4 atm legyen a belső nyomás. Ahhoz, hogy a tömlő szelepén átnyomjuk a levegőt 0.1 atm-val nagyobbnak kell lenni a nyomásnak a pumpában mint a tömlőben. Mekkora hőmérsékletre melegszik a levegő a pumpában, mielőtt a szelep nyílik? A levegő 2 atomos gáz legyen.Mennyivel nő a pumpában lévő 250 köbcenti levegő belső energiája a sűrítés alatt? Mekkora munkát végzünk a pumpában lévő 225 köbcenti levegőn a sűrítés alatt? Mekkora átlagos erővel kell nyomni a 20 centis löketű pumpát? Előre is köszönöm!

2005 6-os maradéka 1, így az ismétlődő 6 számjegy első jegyét kell venni, azaz 4 a keresett 2005-ik számjegy..

jo mind1 nem kell de ha mágis levezetné nekem még ma valaki akkor a freemailomraa küldjétek el előrree köszönöm de nem kell levezetni csak ha valaki nagyon ráér akkor nem lenne bajjj ha elküldenétek mégeyszer köszi

Köszönöm szépen és le is vezetnétek nekem ?

Köszönöm szépen a segitségedet. Nem elsőéves matekházi, csak érdekeltek a feladatok, még egyszer köszi. :-)

Remélem, nem elsőéves algebra házi feladatokat oldottam meg.:P

2. Ez sokkal könnyebb, tetszőleges két elem összeszorzásánál egyszerűen felírod mindkettőt a generátorelemekből, aztán azokat kicserélgeted a feltétel szerint, így előre hozhatod a második tényezőt.

1. Legyen R egységelemes gyűrű, jelöljük e-vel az egységelemét. Tegyük fel, hogy R ideál az S gyűrűben. Legyen :SS a következő: (s)=s-se. Belátjuk, hogy homomorfizmus. Az additivitás nyilvánvaló: (s₁+s₂)=s₁+s₂-(s₁+s₂)e=s₁-s₁e+s₂-s₂e=(s₁)+(s₂). A multiplikativitás csak egy szemernyivel nehezebb: (s₁s₂)=s₁s₂-s₁s₂e=s₁s₂-s₁s₂e-s₁es₂+s₁es₂e=(s₁-s₁e)(s₂-s₂e); itt használtuk, hogy s₁es₂=s₁es₂e, de ez azért igaz, mert e egységelem R-ben, s₁es₂ pedig R-beli, mert R ideál S-ben. Jelöljük ekkor az képét (ez egy részgyűrű) T-vel. Állítjuk, hogy T direkt kiegészítő S-ben R-hez. Ugyanis tetszőleges sS-re s=(s)+se, vagyis minden felbomlik. Másrészt ha s-se=tT R-ben is benne van, akkor, akkor s=t+se R-beli elem (mivel seR, hiszen R ideál), azaz s=se (e egységelem R-ben), így a közös elem csak a 0 lehet.