| [1172] leni536 | 2010-05-20 14:57:55 |
 X N(64,162) N(64,162)
Ez ugye egy pontszám alakulásának a valószinűségi változója. Tudjuk, hogy egy diák 0,1 valószínűséggel bukik meg. Legyen x0 a bukás ponthatára, így:
P(X<x0)=0,1
Standardizálva az X-et:
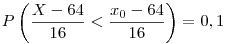
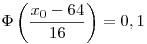
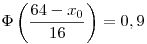
A standard eloszlást táblázatából:
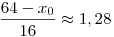
x0 43,52 43,52
Tehát jó közelítéssel 43 ponttal még buknak, 44-gyel már nem.
|
| Előzmény: [1171] Yvi, 2010-05-20 13:25:08 |
|
| [1171] Yvi | 2010-05-20 13:25:08 |
 Nagyon köszönöm, ha lehet, itt van még egy feladat ami nagyon nem megy: Egy osztály teszteredményeinek normál eloszlásának átlaga 64, szórása 16. Találja meg a legkisebb osztályzatot, ami még nem jelent bukást, hogyha a legrosszabb 10százalék bukik meg. Ezt meg próbáltam kiszámolni, hogy 1-P(X<x)=0.1 de valamit biztos elrontottam,mert mínusz érték jött ki. b.) feladat: Ha minden diák 60 és 70 pont között hármast kapott, és tudjuk, hogy pontosan 10 diák kapott hármast, hány diák írta meg a tesztet?
|
|
| [1170] Maga Péter | 2010-05-20 08:36:57 |
 Egy egész szám 5-nél kisebb távolságra van a 4-től pontosan akkor, ha nemnegatív, és legfeljebb 8. Innen az 5. A Csebisev' elvben csak azt engedné meg, hogy 4-et írj, de az egészértékűség miatt ezt fel tudod nyomni 5-re, és így erősebb becslést kapsz.
|
| Előzmény: [1169] Yvi, 2010-05-20 02:24:57 |
|
| [1169] Yvi | 2010-05-20 02:24:57 |
 Sziasztok, lenne egy valszám feladat amit nem értek: Egy telefonközpont napi 2000 hívást kap,annak a valószínűsége,hogy egy hívás téves, az 0.002.(független események) Mi a valószínűsége annak, hogy a 2000ből maximum 8 hívás téves? A megoldókulcs szerint ez binomiális eloszlás, illetve utána Csebisev egyenlőtlenséget kell használni. Ami leginkább nem világos, hogy mi az az 5 ott? (Elnézést, hogy ilyen halványak a vonalak, azért remélem látszik a lényeg)
|
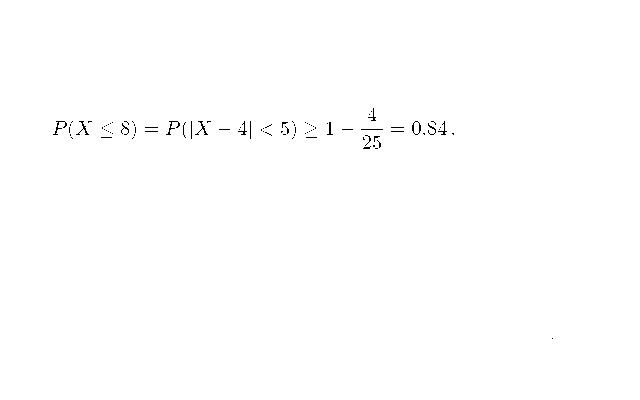 |
|
| [1168] Fernando | 2010-05-19 22:52:58 |
 Egyébként nyugi, maga Student (akit persze nem Studentnek hívtak:) is elszámolta annak idején az eloszlást.
Dolgozatban lineáris interpoláció a táblázati értékekre és kész.
Persze meg lehet próbálni definíció szerint is kiszámolni, vagy inkább kiszámoltatni számítógéppel és akkor kiderül, hogy mennyi az annyi. :)
|
| Előzmény: [1146] mologa, 2010-05-17 18:35:14 |
|
| [1167] Sirpi | 2010-05-19 11:46:44 |
 FF
(Egyébként nem tudod a win2000-et virtuális operációs rendszerként futtatni? Mert használhatnál fő oprendszerként bármit, amit szeretnél, és csak a speckó programodhoz, ami igényli a win2000-et, indítanád el a virtuális gépet.)
|
| Előzmény: [1166] HoA, 2010-05-19 10:57:33 |
|
| [1166] HoA | 2010-05-19 10:57:33 |
 Egyik gépepen meg kell tartanom a Windows2000 op. rendszert. Az Internet Explorer viszont már nem jó például a youtube-hoz. Hogy ne kelljen sokat kisérletezgetnem, tudja valaki, van-e olyan böngésző, ami megfelel az új követelményeknek és Windows2000 alá telepíthető?
|
| Előzmény: [1161] Róbert Gida, 2010-05-18 10:03:48 |
|
| [1164] Fernando | 2010-05-18 16:35:57 |
 Bár azt gondolom, hogy a pszichológiai szempontból pontatlan volt amit írtál, de ez mit sem változtat a dolog igazságtartalmán. Persze a dolog messzire vezetne nagyonis.
Röviden szólva a társadalom egyszerűen nem áll a tanárok mögött.
|
| Előzmény: [1162] bily71, 2010-05-18 11:02:52 |
|
| [1163] SmallPotato | 2010-05-18 13:38:38 |
 Na jó ... azért a helyzet nem ennyire egyszerű. Normális oktatás ma is van. A (vélt vagy valós) demokrácia ugyan kissé sajátossá tette a viszonyokat - de a jelen esetben inkább a tapasztalatból adódó különbségről beszélhetünk.
(Lásd HoA - jogos - észrevételét a fiatal versenyző elriasztásával kapcsolatosan. :-) )
|
| Előzmény: [1160] mologa, 2010-05-18 08:46:23 |
|
| [1162] bily71 | 2010-05-18 11:02:52 |
 A régi időkben az oktató egyik hatásos eszköze a fegyelmezés volt, mely része a nevelésnek, ugyanúgy, mint az oktatás. A mai törvények ezt az eszköszt kivették a tanárok és a gyámhivatal kezéből és olyan jogokkal ruházzák fel a gyermekeket, melyek egyszerűen nem illetik meg őket.
|
| Előzmény: [1161] Róbert Gida, 2010-05-18 10:03:48 |
|
|
|
| [1159] HoA | 2010-05-18 08:37:48 |
 Ne riaszd el a fiatal versenyzőt ha ilyen problémái vannak.
Lineáris kapcsolatot feltételezve ha a szabadságfok 40-ről 30-ra változik az érték pedig 21 ezrelékkel nő, akkor a 40 --> 37 változáshoz ennek 3 tizede , azaz 6,3 ezrelék , a táblázat pontosságát figyelembe véve kerekítéssel 6 ezrelék tartozik, így a keresett érték 2,027.
|
| Előzmény: [1157] SmallPotato, 2010-05-17 22:17:44 |
|
| [1158] SmallPotato | 2010-05-17 22:38:22 |
 A táblázati értéktől való eltérés két okból adódhat: egyrészt a közrefogó adatok pontossága véges (magyarán pl a 2,042 elvileg lehet akár 2,0415 vagy efféle és a 2,021 is lehet 2,0205, másrészt az összefüggés nem egészen lineáris (a 2,042 környékén láthatólag nagyobbak a lépések, mint a 2,021 környékén).
|
| Előzmény: [1157] SmallPotato, 2010-05-17 22:17:44 |
|
|
|
|
|
| [1153] Higgs | 2010-05-17 20:56:56 |
 Köszönöm Jonas, hasznos volt a link! Most a következő a kérdésem: m0(0 jobb alsó indexbe) nyugalmi tömegű relativisztikus részecske ugyanolyan nyugalmi tömegű álló részcskének ütközik tökéletesen rugalmatlanul. Mekkora a keletkező részecske tömege Lorentz faktorral kifejezve?
|
|
|
|
|
| [1149] mologa | 2010-05-17 18:38:32 |
 Hogy lehet bemásolni a képleteket is ide?:)
|
|
|
| [1147] mologa | 2010-05-17 18:36:17 |
 nem tud rendesen bemásolodni :((
|
|



 N(64,162)
N(64,162)  43,52
43,52