| [1200] Fernando | 2010-05-26 20:22:34 |
 A k=2 eset nagyon ismert Dr. Németh József tanítványai körében. :) Nekem a legjobban Euler bizonyítása tetszik, igaz ott jónéhány lépés létjogosultsága kérdéses. Németh József: Előadások a végtelen sorokról (Polygon): ebben olvasható vagy három biz.
|
| Előzmény: [1173] D. Tamás, 2010-05-20 19:08:29 |
|
| [1199] mologa | 2010-05-26 18:03:26 |
 Igazolja, hogy a minta normális eloszlású Adja meg a khi2 statisztika értékét ha az osztályok száma öt?
-1.48 , -1.48 , -1.45 , -1.06 , -1.05 , -1.04 , -1.04 , -0.94 , -0.94 , -0.75 , -0.70 , -0.55,-0.53 -0.48 , -0.38 , -0.09 , -0.05 , 0.04 , 0.05 , 0.11 , 0.18 , 0.19 , 0.32 , 0.36 , 0.48 , 0.51 , 0.60 0.70 , 0.70 , 0.83 , 1.30 , 1.50 , 2.08
minta elemszáma n = 33 átlag= -0,123 osztályok száma r=5 egy osztály szélessége Scsillag=0.8886 Scsillag= korrigált tapasztalati szórás :)) Az osztály szélességre miért a korrigált tapasztalati szórást veszi?
Osztály közök minusz végtelen-1.4559 -1,4559, -0,5673 -0,5673, -0,3212 -0.3212, -1,2099 -1,2099, minusz végtelen
Az osztály közök miért igy alakultak? Ezt nem értem:)
|
|
| [1198] mologa | 2010-05-26 16:58:47 |
 Sirpi elküldtem neked emailbe :)
|
|
| [1197] mologa | 2010-05-26 16:51:34 |
 uhhhh ez össze vissza mászott :))
|
|
| [1196] mologa | 2010-05-26 16:49:44 |
 2. Igazolja, hogy a minta normális eloszlású Adja meg a khi2 statisztika értékét ha az osztályok száma öt?
-1.48 , -1.48 , -1.45 , -1.06 , -1.05 , -1.04 , -1.04 , -0.94 , -0.94 , -0.75 , -0.70 , -0.55,-0.53 -0.48 , -0.38 , -0.09 , -0.05 , 0.04 , 0.05 , 0.11 , 0.18 , 0.19 , 0.32 , 0.36 , 0.48 , 0.51 , 0.60 0.70 , 0.70 , 0.83 , 1.30 , 1.50 , 2.08
minta elemszáma n = 33 A becsült paraméterek (átlag)=-0.123 korrigált szórás S csillag= 0.8886 Az osztályok száma r = 5
Egy osztály szélessége S csillag= 0.8886 Az osztály szélességre miért a (szórást) 0.8886 ot veszi?
Osztály közök Pi nPi
- - 1.4559 2 0.0668 2.2044 0.0190
-1.4559, -0.5673 9 0.2417 7.9761 0.1344
-0.5673, -0.3213 12 0.3830 12.639 0.0323 -0.3213, -1.2099 7 0.2417 7.9761 0.1195
-1.2099, - 3 0.0668 2.2044 0.2871 khi2=0.5893 Az osztályközök értéki miért igy jöttek ki? Ezt nem értemL Valaki levezeti
|
|
|
| [1194] mologa | 2010-05-26 16:40:15 |
 Sajnos nem tudom bemásolni a word-ben irt feladatot. Mig TeX-ben irnám meg kirügyeznék:))
|
|
|
|
|
| [1190] Hölder | 2010-05-23 23:49:40 |
 Sziasztok! Azon gondolkodtam el,hogy ha 2(n)+1 prim (kitevőben van az n), akkor n kettő hatvány (Fermat primek),de forditva igaz -e, azaz, ha n kettőhatvány,akkor 2(n)+1 prim, megnéztem egy jó ideig,addig igaz volt,az a sejtésem, hogy nem az.
|
|
|
|
|
|
| [1185] jonas | 2010-05-21 11:56:08 |
 A Poisson közelítést a binomiális eloszlásra akkor lehet használni, ha várhatóan kevés rossz üveg készül, például abban az esetben, amit Sirpi javasolt.
|
| Előzmény: [1182] Yvi, 2010-05-20 23:38:21 |
|
| [1184] Maga Péter | 2010-05-21 11:43:15 |
 A páros esetben  (2k)= (2k)= 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen  (3), (3), (5),... a kérdéses értékek, ezek tetszőleges pontossággal kiszámolhatók, akár a (5),... a kérdéses értékek, ezek tetszőleges pontossággal kiszámolhatók, akár a  , az e, a , az e, a  (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a  páratlan értékei, illetve ha nem, akkor esetleg más konstansokkal ( páratlan értékei, illetve ha nem, akkor esetleg más konstansokkal ( , e stb.) összefüggésbe hozhatók-e. A , e stb.) összefüggésbe hozhatók-e. A  -ról sem tudjuk, hogy racionális-e, és azt sem tudjuk, hogy -ról sem tudjuk, hogy racionális-e, és azt sem tudjuk, hogy  +e racionális-e (ha az lenne, akkor az e ugyanúgy kifejezhető lenne a +e racionális-e (ha az lenne, akkor az e ugyanúgy kifejezhető lenne a  -ből, mint a -ből, mint a 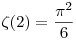 ), mégsem használjuk egyikre sem, hogy nem ismert. ), mégsem használjuk egyikre sem, hogy nem ismert.
|
| Előzmény: [1176] jenei.attila, 2010-05-20 19:36:13 |
|
|
| [1182] Yvi | 2010-05-20 23:38:21 |
 A binomiális eloszlással hogy jött ki a 803? Tényleg nem Poisson, csak elnéztem, az volt, oda írva, hogy a Poisson közelítést kell használni. Ez jelenti azt, hogy np=lambda?
|
| Előzmény: [1177] jonas, 2010-05-20 21:39:13 |
|
| [1181] jonas | 2010-05-20 22:57:29 |
 Persze nem kell nagyon komolyan venni ezt a tankönyvi példát, mert a válasz nagyon érzékeny az adatokra, mint pl. a szórás pontos értékére, a sör mennyiségének az eloszlására, meg az egyes üvegek függetlenségére. Ha egy kicsit módosítod a számokat, kaphatsz 0.1-et vagy 0.999-et is eredménynek.
|
| Előzmény: [1180] jonas, 2010-05-20 22:51:22 |
|
|
| [1179] Sirpi | 2010-05-20 22:40:07 |
 Szerintem el lett írva az átlag (51 helyett 50 kellene), mert úgy szimmetrikus a két határszám (48,9 és 51,1). És úgy valószínűleg értelmes lesz az eredmény is, ami kijön.
|
| Előzmény: [1177] jonas, 2010-05-20 21:39:13 |
|
| [1178] Higgs | 2010-05-20 22:20:09 |
 http://www.newscientist.com/article/dn18886-impossible-motion-trick-wins-illusion-contest.html
A valóságban is ezt a hatást keltené?
|
|
| [1177] jonas | 2010-05-20 21:39:13 |
 Ezt két lépésben kell megoldani. Először azt kell kiszámítani, hogy egy üveg sör mikor lesz hibás.
Annak a valószínűsége, hogy 48.9-nál kevesebb sör van az üvegben, elhanyagolhatóan kicsi, viszont mivel az átlag közel van, az 51.1-nél több sörnek egy üvegnél kb. 0.401 a valószínűsége. (Itt nyilván azt tettük föl, hogy a sör űrtartalma normális eloszlású.)
Ezért aztán a napi 2000 üvegből átlagosan 803 hibás van, tehát a binomiális eloszlást nem Poisson, hanem normális eloszlással kell közelíteni. Annak a valószínűsége, hogy 20-nál kevesebb túl nagy üveg sör készül, e miatt nagyon kicsi (értsd: előbb romlik el a gép), ha jól számolok, akkor 5.10-556 nagyságrendű.
(Nem vagyok túl jó statisztikából, úgyhogy valaki ellenőrizze a számításaimat.)
|
| Előzmény: [1175] Yvi, 2010-05-20 19:17:32 |
|
| [1176] jenei.attila | 2010-05-20 19:36:13 |
 A első probléma a Bernoulli-féle hatványösszeg probléma, amelyre egy nagyon szép levezetést találhatsz pl. Dörrie A diadalmas matematika c. könyvében. Egyébként magad is könnyen levezetheted, ha feltételezed, hogy a k-adik hatványok összege n-nek (a tagszámnak) egy k+1-ed fokú polinomja. Ekkor a polinomot határozatlan együtthatókkal felírva, n helyére 1,2,...k+2-őt helyettesítve, egy lineáris egyenletrendszert kapsz az együtthatókra. Az hogy a zárt képlet n-nek k+1-ed fokú polinomja, könnyen látható abból, hogy pk(n+1)-pk(n)=nk (ahol pk(n) a zárt alak n tagra) egy k-ad fokú polinom. Márpedig egy k+1-ed fokú polinom két egymás melletti természetes számon felvett helyettesítési értéke k-adfokú polinom. Tehát ha a fenti egyenletrendszernek van megoldása, akkor az megadja a zárt képletet is. Ennél egy lényegesen szellemesebb levezetést találsz az említett könyvben. A második probléma jóval nehezebb, és semmi köze az elsőhöz. Tudomásom szerint páros k-kra ismert zárt alak (k=2-re Euler adta meg először), míg páratlanokra nem ismert (ha nem így van, nyugodtan javítsatok ki).
|
| Előzmény: [1173] D. Tamás, 2010-05-20 19:08:29 |
|







 (3) rac. együtthatós polinomjaként kifejezhető páratlan k-kra is
(3) rac. együtthatós polinomjaként kifejezhető páratlan k-kra is 
 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen
2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen  (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a
(Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a 