Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[1262] Huszár Kristóf

2010-07-05 14:44:10

Szia Jedy!

huszar[PONT]kristof[KUKAC]gmail[PONT]com

Remélem, tudok segíteni.

Előzmény: [1259] Jedy, 2010-07-04 17:00:31

[1261] Róbert Gida

2010-07-04 21:26:35

Mi az, hogy legoptimálisabb? Optimálisnál jobb, vagy mi a túró?

Amúgy eddig egyetlen több, mint 80,000-es *városra* oldották meg a TSP-t. A TSP-re egy rakás heurisztika működik, az Eternity 2-nél pedig backtracking-nél nincs nagyon jobb, jelenleg.

Előzmény: [1260] Higgs, 2010-07-04 18:15:55

[1260] Higgs	2010-07-04 18:15:55
Üdv! A következő nem világos. Már ismert olyan algoritmus ami több mint 80.000 város legoptimálisabb bejárását megadja, de a 256 darabból álló Eternity 2-őt nem tudta eddig senki megoldani.

[1259] Jedy

2010-07-04 17:00:31

Hello Kristóf!

Nem tudom elkérhetném-e az e-mail címedet,hogy néhány kérdéssel zaklassalak?Előre is köszi.

Előzmény: [1258] Huszár Kristóf, 2010-07-04 14:49:09

[1258] Huszár Kristóf	2010-07-04 14:49:09
Sziasztok! Most fejeztem be az első évemet az ELTE matematika BSc. szakán és nagyon pozitívak a tapasztalataim. Mindenkinek, aki ilyen irányban gondolkozik csak ajánlani tudom. Szép nyarat :)

[1257] psbalint	2010-07-04 09:30:13
A Müncheni Műszaki Egyetem a legjobb műszaki egyetem német nyelvterületen, kivéve az ETH Zürichet.

[1256] vogel	2010-07-03 21:40:46
Elég nyilvánvaló, hogy gagyi nem lehet... Mintha a magyar nem lenne (neked) elég színvonalas. (bsc-s tapasztalat nélkül)
Előzmény: [1255] Jedy, 2010-07-03 21:24:17

[1255] Jedy	2010-07-03 21:24:17
http://www.ma.tum.de/Studium/Studiengaenge szerintetek a Müncheni Műszaki Egyetem Finane and Actuarial Science és Operations Reseaech képzései magas színvonalat nyújthatnak?Esetleg ezekről valakinek nincsenek információi?

[1254] Róbert Gida

2010-07-02 17:45:44

"Ti mit ajánlotok nekem,egy bsc matek szak után"

Msc matek?

Előzmény: [1252] Jedy, 2010-07-02 11:08:47

[1253] psbalint

2010-07-02 14:45:13

Szia! Német nyelvterületen nagyon sok helyen találsz Wirtschaftsmathematik BSc képzéseket, angolul Mathematics in Economics. Magyarországon egyértelműen a BCE-KTK-n a Gazdaságelemzés BSc a legjobb ilyen szak. Vagy ami neked talán még jobban tetszene, van az ELTE-n és a BCE-n közös Biztosítási és pénzügyi matematika mesterszak, erre a gazdaságelemzésről és az ELTE matekról is ugyanolyan jó eséllyel pályázhatsz. Ezt német nyelvterületen is megtalálod sok helyen Finanz- und Versicherungsmathematik néven, de míg Magyarországon csak mesterkepzésben van (tudtommal), kint alapképzésben is akad. én ide járok http://www.math.tuwien.ac.at/

[1252] Jedy

2010-07-02 11:08:47

Sziasztok!

Igazából az szte-re szeretnék bsc matekra,menni de alapjába véve a közgazdaság érdekel.Ti mit ajánlotok nekem,egy bsc matek szak után mivel érdemes foglalkoznom,hova érdemes tanulni mennem (esetleg külföldön is elsősorban német nyelvterülten)?

[1251] Tóbi	2010-07-01 15:27:34
Szerintem itt minden kérdésedre megtalálod a választ.
Előzmény: [1250] Jedy, 2010-07-01 08:46:50

[1250] Jedy

2010-07-01 08:46:50

sziasztok!

Merőben új témáról szeretnék kérdezni,hátha valaki nagyobb tudással rendelkezik ezen a téren.Valaki tudja pontosan,hogy kiből is lehet kockázatelemző,és alapjába véve mit is csinál?Bármilyen információt szívesen fogadnék.Köszönöm:)

[1249] Lóczi Lajos	2010-06-25 23:26:49
Nem, akkor nem tudunk.
Előzmény: [1248] Fernando, 2010-06-25 18:37:09

[1248] Fernando

2010-06-25 18:37:09

Köszönöm!

Másik kérdés: ha a kiválasztási axiómát nem fogadjuk el, akkor is tudunk konstruálni nem L-mérhető halmazt?

Előzmény: [1238] Maga Péter, 2010-06-20 18:09:54

[1247] jonas	2010-06-23 12:16:04
Igen, én is zöldségeket írok.
Előzmény: [1246] nadorp, 2010-06-23 08:01:57

[1246] nadorp	2010-06-23 08:01:57
Nem Gauss kvadratikus reciprocitás tétel ?
Előzmény: [1243] jonas, 2010-06-22 18:10:40

[1245] S.Ákos	2010-06-22 21:32:54
Köszönöm, sikerült (megint) elírnom, amire gondoltam.
Előzmény: [1243] jonas, 2010-06-22 18:10:40

[1244] Róbert Gida	2010-06-22 18:38:32
Euler kritérium ellenőrzéséhez nem kell semmilyen prímfelbontást meghatároznod.
Előzmény: [1243] jonas, 2010-06-22 18:10:40

[1243] jonas

2010-06-22 18:10:40

Hadd foglaljam röviden össze a helyzetet, mert volt némi keveredés.

Bármilyen p prímre az 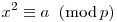$x^2 \equiv a \left.\right.(\mod p)$ kongruencia a számok kb. felére oldható meg (a p-hez nem osztható számoknak pontosan a felére, plusz még a p-vel osztható számokra). Összetett számokra nem ez a helyzet, itt több a számra nem oldható meg a kongruencia, mivel lényegében szétesik több másodfokú kongruenciára minden prímosztóra; hogy hány a-ra van megoldás, az így a p prímfelbontásából könnyen kiszámolható.

A p négyes maradéka abban segít, hogy eldöntsd, konkrétan x² $\equiv$ -1 megoldható-e. Van arra is elmélet, hogyan lehet meghatározni, hogy egy bizonyos a-ra és p-re meg lehet-e oldani a kongruenciát, ehhez „csak” néhány (max (|a|,|p|)-nél kisebb vagy egyenlő) szám prímfelbontását kell tudni kiszámolni. Ebből az is következik, hogy rögzített a-ra és változó p prímekre a megoldhatóság csak p-nek a 4a-s osztási maradékától függ. Ez az Euler-féle kvadratikus reciprocitási tételen alapul, számelmélet kurzuson tanítani szokták, és le van írva a remek Erdős–Surányi-féle Válogatott fejezetek a számelméletből könyvben.

Előzmény: [1242] Róbert Gida, 2010-06-22 13:08:09

[1242] Róbert Gida

2010-06-22 13:08:09

Egyre zöldebbeket írtok. Ha például a=1, akkor a kongruencia mindig megoldható, még az sem kell, hogy p prím.

Amúgy a kongruencia pontosan akkor oldható meg, ha 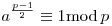$a^{\frac {p-1}{2}} \equiv 1 \mod p$ , illetve, ha a osztható p-vel. (Ez van páratlan p prím esetén, p=2-re mindig van megoldás.) Mellesleg ez az Euler kritérium.

Előzmény: [1241] m2mm, 2010-06-22 10:22:42

[1241] m2mm	2010-06-22 10:22:42
szerintem p maradéka mod 4. 4k+1 alakú prímekre mindig megoldható, 4k-1 alakúra nincs megoldás. A tételnek szerintem nincs külön neve.
Előzmény: [1240] Róbert Gida, 2010-06-21 23:28:11

[1240] Róbert Gida	2010-06-21 23:28:11
p maradéka mod 4p az ránézésre p. De nem egészen értem a kérdést.
Előzmény: [1239] S.Ákos, 2010-06-21 19:19:55

[1239] S.Ákos

2010-06-21 19:19:55

Üdv!

Valaki tudja, hogy mi a neve a következő tételnek: Az x² $\equiv$ a(mod p) kongruencia akkor és csak akkor oldható meg (p prím), ha p maradéka egy (mod 4p) meghatározott halmazba tartozik?

[1238] Maga Péter	2010-06-20 18:09:54
Sőt, tetszőleges L^p-ben is igaz ez p>1-re (Hunt, nem sokkal Carleson után). A vicces az, hogy disztribúciós értelemben L¹-beli függvényhez is konvergál a Fourier-sora, ez nem nehéz, csak a fogalmakat kell ismerni.
Előzmény: [1237] Tassy Gergely, 2010-06-20 15:06:25

Már regisztráltál?
Új vendég vagy?