| [1350] bily71 | 2010-09-20 17:03:25 |
 Eszembe jutott egy régebbi vitánk a Brun-állandóról. Továbbra is fenntartom, hogy amig nem tudjuk, hogy az ikerprimek száma véges-e, avagy végtelen, addig felesleges, sőt butaság vizsgálni a Brun-állandó racionális, vagy irracionális voltát. Egy sorozat összegéről csak akkor tételezetjük fel, hogy irracinális, ha már tudjuk, hogy az végtelen sok tagból áll.
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
| [1349] bily71 | 2010-09-20 16:49:38 |
 Mondjuk B első számjegye 1, a második 4, a harmadik 1,... vagyis B a  soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta. soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta.
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
|
| [1347] jonas | 2010-09-20 15:27:34 |
 Hmm, akkor most már én is mondok igazi segítséget. Fannka: a házi feladatokhoz általában segít valamelyik korábbi (órai vagy házi) feladat. Nézd át az előző heti feladatsort, és a megoldásokat, és találd ki, melyik kettő illik ide. Ha nem tudod a megoldást a megfelelő feladatokra, akkor próbáld meg először azokat megoldani; ha nem megy, kérdezz meg valakit, aki bent volt az órán, és jegyzetelt. (Nagy általánosságban a nők jobban jegyzetelnek az egyetemi órákon, mint a férfiak, de sok egyéni különbség van.)
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
| [1346] Sirpi | 2010-09-20 15:20:55 |
 Képzeld azt, hogy az első számjegyet 1/2, a 2.-at 1/4, a 3.-at 1/8, stb. másodperc alatt írják a szám végére (mindig feleződik az idő). Ekkor 1 másodperc után elő is áll a végeredményként kapott szám. És ha B nem onnan kapta a nevét, hogy hihetetlenül B-na, akkor nagyon könnyen el tudja érni, hogy ez irracionális legyen (egyelőre nem lövöm le).
|
| Előzmény: [1342] bily71, 2010-09-20 14:51:06 |
|
|
| [1344] HoA | 2010-09-20 14:57:53 |
 Arra gondolsz, hogy ne mi oldjuk meg a házi feladatait? Ha igen, akkor amit leírtam, ugyanúgy csak segítség, mint a javaslat az 1 kút, 2 kút, stb. megközelítéshez. A bizonyításhoz igazolni kell a grafikon említett tulajdonságait.
Vogel hozzászólásából nem látom, miért ne adhatnánk ötleteket, hisz ő is ad, meg te is. Vagy másra gondoltál? Lehet, hogy tudnom kéne, mi az az fmx ?
|
| Előzmény: [1341] jonas, 2010-09-20 14:37:24 |
|
|
| [1342] bily71 | 2010-09-20 14:51:06 |
 J-nek van nyerő stratégiája, ugyanis ahhoz, hogy ez a szám irracionális legyen végtelen sok tizedesjegyet kell leirni, vagyis a játék sosem ér véget. Ha eltekintünk attól az apróságtól, hogy az ember élete véges és vég nélkül folytatódik a játék, B akkor sem nyerhet, mert akárhányadik lépésnél is tart, a tizedesjegyek száma mindig véges.
|
| Előzmény: [1340] jonas, 2010-09-20 14:27:57 |
|
| [1341] jonas | 2010-09-20 14:37:24 |
 HoA, csak azért segítsz neki, mert ő is kutya fényképeket rak föl, vagy pedig nem láttad, hogy vogel mit írt? Csak kíváncsiságból kérdezem.
|
| Előzmény: [1339] HoA, 2010-09-20 12:12:42 |
|
|
| [1339] HoA | 2010-09-20 12:12:42 |
 Erre a feladatra van egy egyszerű, szemléletes megoldás, ha már szóba került leírom: Képzeljünk az autóra egy póttankot, az egész pályára elegendő benzinnel. Valamelyik kúttól indulva rajzoljunk egy grafikont, ami az autóban lévő benzin mennyiségét mutatja a megtett út függvényében. Az induló kútnál megugrik a kút tartalmával, utána a következő kútig egyenletesen csökken, itt megint helyben nő ennek a kútnak a tartalmával, és így tovább. Egy fűrészfogazás jellegű ábrát kapunk. A feltétel miatt a kiinduló kúthoz visszaérve pont annyi benzin lesz az autóban, mint induláskor. Lehet, hogy lesznek olyan pontok, ahol a benzin a kezdeti szint alatt van, vagyis a póttankból fogyasztunk.
Nézzük meg, hogyan változik a grafikon, ha egy másik kúttól indulunk. A menete ugyanaz, csak függőlegesen el lesz tolva, felefelé vagy lefelé - és persze az elejéről egy darab a végére kerül. A megoldás: A tetszőleges kúttól induló grafikonon válasszuk ki a legmélyebb pontot. Ez nyilván valamelyik kúthoz történő érkezésnél van. Ettől a kúttól indulva a grafikon végig a póttank szintje felett halad, a póttank elhagyható.
|
| Előzmény: [1335] Fannka, 2010-09-19 21:06:18 |
|
|
| [1337] Fannka | 2010-09-19 22:35:44 |
 szabad tudnom ki vagy, Vogel?:P már csak azért is h tudjam, ki tengeti a vasárnap estéit rajtam kívül KöMaL fórumon:) meg h mennyire égtem le itt...
|
 |
|
| [1336] vogel | 2010-09-19 21:27:52 |
 Először vizsgáld meg 1 kútra, 2 kútra... 2 kút esetén el lehet indulni egy kútból úgy, hogy tovább mehess egy másik kúthoz? Stb. Ha semmiképp sem megy, inkább konzultálj/gondolkodj a társaiddal az fmx (:-P) házikról, mert mindenre nem fogsz itt választ kapni.
|
| Előzmény: [1335] Fannka, 2010-09-19 21:06:18 |
|
| [1335] Fannka | 2010-09-19 21:06:18 |
 Egy kör alakú autópálya mentén benzinkutak vannak, bennük különböző mennyiségű benzin. Tudjuk, hogy összesen pont annyi benzin van szétosztva a kutak közt, amennyi egy kör megtételére elég. Bizonyítsuk be, hogy van olyan pontja a pályának, ahonnan egy autó üres tankkal elindulva végig tud menni a kutakban található benzin segítségével.
|
 |
|
|
| [1333] Fannka | 2010-09-19 20:43:13 |
 J És B felváltva írnak a tizedesvessző után számjegyeket végtelen sokáig. J nyer, ha a kapott szám racionális, B ha irracionális. Kinek van nyerő stratégiája? (ui: és köszi az előző megoldásokat:)
|
 |
|
|
| [1331] tamas553 | 2010-09-19 12:14:42 |
 Van két kitérő egyenesünk a térben:
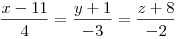

Mekkora a két egyenes távolsága?
|
|
| [1330] Kristóf Miklós 2 | 2010-09-18 16:33:47 |
 Kedves Jonas, köszönöm kedves válaszod, végre láttam egy egyszerűbb megoldást. Nekem ennél bonyolultabb jött ki. Bizonyára azért olyan népszerű, mert egyszerűen megfogalmazható, mégse egyszerű a megoldás.
|
| Előzmény: [1329] jonas, 2010-09-17 11:26:31 |
|
|
| [1328] Kristóf Miklós 2 | 2010-09-17 09:51:37 |
 Kedves Mindenki! Van egy aranyos feladatom, amit szeretnék megosztani veletek.
Van egy r sugarú legelő, és az egyik széléhez ki van kötve egy kecske. A kötél hossza R. A kecske mindent lelegel, amit elér. Milyen hosszú a kötél, ha a kecske a legelőnek épp a felét legeli le?
Adjuk meg 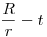 10 jegy pontosan! 10 jegy pontosan!
|
|
| [1327] jonas | 2010-09-16 17:09:58 |
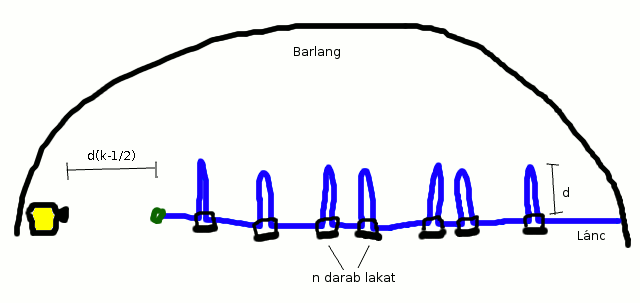
 Én meg tudom csinálni n+1 lakattal is, bármi legyen is a k.
Rögzítsük a barlang egyik oldalához a kincsesládát, ezen legyen egy lakat. A lakat kulcsát rögzítsük egy hosszú láncra a barlang másik végéhez. A láncot n darab lakattal rövidebbre vesszük úgy, hogy minden rablóhoz pontosan egy lakatja van, és ehhez csak neki van kulcsa. Minden lakat két, egymástól d távolságra lévő láncszembe van beakasztva, és a lefogott d hosszú darabok nem fedik át egymást. A lánc hossza úgy van beállítva, hogy ha k lakatot kinyitnak, akkor már a végén lévő kulcs eléri a kincsesláda lakatját, de ha csak k-1-et nyitnak ki, akkor nem.
|
 |
| Előzmény: [1326] Róbert Gida, 2010-09-16 15:54:30 |
|
| [1326] Róbert Gida | 2010-09-16 15:54:30 |
 Még ennél is van jobb, ha nem egy szimplán leüthető lakatról van szó, hanem egy elektronikusról. Legyen N egy nagy pozitiv egész szám, a kulcs ami a széfet nyitja pedig egy random [N/2,N) intervallumba eső R egész. Az i-edik alkalmazott kulcsa az Rmod pi szám, ahol 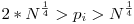 és pi prím (különbözőek). Bármely 4 összeáll, akkor ki tudják nyitni a zárat a kínai maradéktétel miatt (az elektronikus zár kiszámolja R-et a kínaiból), de bármely 3 még nem. és pi prím (különbözőek). Bármely 4 összeáll, akkor ki tudják nyitni a zárat a kínai maradéktétel miatt (az elektronikus zár kiszámolja R-et a kínaiból), de bármely 3 még nem.
|
| Előzmény: [1325] jonas, 2010-09-16 13:30:35 |
|



 soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta.
soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta.








