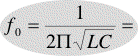|
|
| [133] waszlavikm | 2007-01-18 20:00:37 |
 Tisztelettel üdvözlök mindenkit!
51 éves vagyok, sajnos régen jártam iskolába. Kérem, ha valaki tud segítsen! Adott egy kör alakú kert. A kör kerületén, azaz a kert szélén, leverünk egy karót, melyhez kötéllel kikötünk egy éhes kecskét. Milyen hosszú legyen a madzag, hogy a kecske, a kert területének a felét legyen képes lelegelni?
Köszönettel: Waszlavik Miklós
|
|
| [132] ^mtk | 2007-01-18 19:26:54 |
 Koszonom!
Az alabbi kepletbol kellene szamitani L-t es C-t. Legyszi segitsetek..aztan egyelore ennyi volt:)
Koszonom!
|
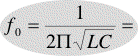 |
| Előzmény: [131] i, 2007-01-17 20:36:47 |
|
|
|
|
|
| [127] i | 2007-01-14 14:08:30 |
 Szívesen :)
|
|
|
| [125] i | 2007-01-14 12:58:20 |
 Az mindegy, csak a végén 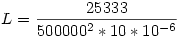 lesz. lesz.
Én az ilyesmit matekórán tanultam valamikor régen, egyenletrendezés címszóval lehetne esetleg rákeresni...
|
|
| [124] ^mtk | 2007-01-14 12:10:50 |
 Eredetileg a nevezoben kellene legyen a : 10*10 a -6.-on. Igy mar maskeppen fog festeni?
Amugy tudnal ajanlani valami anaygot hogy hol tudom ezeket megnezegetni/megtanulni?
Koszonom!
|
| Előzmény: [122] i, 2007-01-13 23:10:38 |
|
|
| [122] i | 2007-01-13 23:10:38 |
 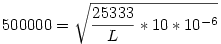
Ezt négyzetre emeled: 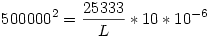
Beszorzol L-lel, és leosztasz 5000002-nel:
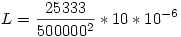
És már csak ki kell számolni :)
|
|
| [121] ^mtk | 2007-01-13 22:47:18 |
 Sziasztok!
En uj vagyok itt .. Nemi segitsegre lenne szuksegem,mivel nem ertem a matematikat,de igyekszem.
A kerdesem a kovetkezo lenne:
f = gyokalatt(n/L*C)
namost egy konkret esetre kellene megoldas.
500000 = gyokalatt(25333/L*10*10 a minusz 6.-on)
Itt L erteket kellene kiszamolni.
Legyszi irjatok le nekem hogy hogy kell,sorrol sorra,ok? Nem muszaly a megoldas csak az elv...( C-re is ugyanaz?)
Koszonom.
|
| Előzmény: [1] Brigi, 2005-08-26 19:45:29 |
|
|
| [119] S.Ákos | 2006-12-31 13:08:45 |
 vki meg tudná mondani, hogy lehet bizonyítást találni arra, hogy
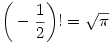
|
|
| [118] HoA | 2006-12-31 11:20:03 |
 A Fórum olvasóinak nagy része valószínűleg ismeri ezt a feladatot. Amiért mégis úgy gondoltam én is, hogy érdemes feltenni a megoldást, az Korea "Milyen stratégiák lehetségesek?" kérdése. Be tudjuk-e bizonyítani, hogy nincs más stratégia, mellyel egy kivételével mindenki biztosan eltalálja sapkája színét ?
|
| Előzmény: [117] jenei.attila, 2006-12-30 20:57:56 |
|
| [117] jenei.attila | 2006-12-30 20:57:56 |
 Megegyezhetnek pl. hogy, ha az utolsó maga előtt páros sok piros sapkát lát, akkor pirosat mond, különben kéket. Eszerint ő 50 százalékos eséllyel találja el a saját fején lévő sapka színét, azonban a többiek már biztosan tudni fogják, mert csak azt kell számon tartaniuk hogy mit mondtak a mögöttük lévők, és mit látnak maguk előtt (természetesen csak a piros sapkák paritása érdekes). Ha pl. az n-edik pirosat mondott, az azt jelenti, hogy 1-től n-1 ig páros számú piros sapka van. Az n-1 edik ember megszámolja a maga előtt látható piros sapkákat, ha ez páros akkor az ő fején kék sapka van, különben piros, s.í.t. Vagyis ezzel a stratégiával csak az n-edik ember mondhat más színt, mint amilyen sapka a fején van.
|
| Előzmény: [116] Korea, 2006-12-30 19:33:35 |
|
| [116] Korea | 2006-12-30 19:33:35 |
 Üdv mindenkinek,és mindenkinek sikerekben gazdag, boldog újesztendőt kívánok. Segítséget kérnék az alábbi feladat megoldásához, mert nekem bizony fogalmam sincs, hogyan kell ezt megoldani. a segítséget előre is köszönöm. Ha valaki tud segíteni, megköszönöm, ha az e-mail címemre is elküldi a megoldást.
A feladat:
n db ember fején véletlenszerűen piros vagy kék sapka van. Egymás mögött állnak, mindenki csak az előtte állókat látja, a saját és mögötte állók sapkáját nem. A sorban utolsónak állótól kezdődően visszafelé mindenki sorban megtippelheti, hogy milyen színű sapka van a fején (vagy kéket, vagy pirosat mondhat). Sorbaállás és sapkahúzás előtt összebeszélhet az n ember, megbeszélhetnek egy közös stratégiát. Milyen stratégiák lehetségesek? Mekkora találatszám várható?
|
|
| [115] Matthew | 2006-12-30 14:49:57 |
 Üdv Mindenkinek!
Van egy problémám:
Az alábbi képen van egy tábla tele gombokkal.Ha az egyik gombot megnyomom,akkor az a gomb,és az oldalaival határos gmbok is zöld színűvé változnak(két oldalán,alatta és fölötte).Hogyan lehet az összes gombot zöld színűre változatni,ha egy zöld színű gombra kattintva az újra feketévé változik,ill.,ha olyan gombra kattintok,amelynek egyik(vagy több) oldalával határos gomb már zöld színű,akkor az szintén fekete lesz?Aki tud,légyszi segítsen!Előre is köszönöm.Mindenkinek boldog újévet kívánok!
|
 |
|
|
|
|
| [111] Sirpi | 2006-12-04 20:44:30 |
 A számtani-négyzetes közepek közti egyenlőséget használva kétszer (vagy a számtani-4. hatványközepest egyszer) rögtön adódik, hogy csak az x=0 megoldás:
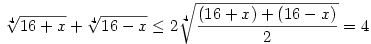 . Egyenlőség csak 16+x=16-x, vagyis x=0 esetén. . Egyenlőség csak 16+x=16-x, vagyis x=0 esetén.
|
| Előzmény: [109] Doom, 2006-12-03 18:55:01 |
|