Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91]

Szeretnél hozzászólni? Jelentkezz be.

[1395] David820607	2010-10-06 16:46:06
Létezik (nem csupa azonos tagból álló) tetszőlegesen hosszú számtani sorozat csupa teljes hatványból?

[1394] Szekér István

2010-10-06 15:44:39

Helló, ez most nem matekos kérdés lesz:

Amikor regisztráltam, majd beléptem, ezt kérdezte: hanyadik osztályba jársz 2009/2010 tanévben (ami a tavalyi tanév volt) kiválasztom, hogy 9. osztály (most 10.-es vagyok), aztán jöttem rá, hogy ez nem jeó. Hogy tudom megváltoztatni az évfolyamom? Regisztráljak újra?

[1393] Csimby	2010-10-02 22:19:07
Nincs mit, te is segíthetsz nekünk a szomszéd topicban :)
Előzmény: [1392] Khesteg, 2010-10-02 22:09:22

[1392] Khesteg	2010-10-02 22:09:22
Eh...tényleg. Nem vettem észre hogy lehet egyszerűsíteni. Köszi szépen a segítséget :)

[1391] Csimby

2010-10-02 19:04:16

Inkább $-\frac{\infty}{\infty}$ az, mint $\frac00$ , de a lényeg hogy a végén lehet egyszerűsíteni:

$\lim{\frac{\ln{x}}{\frac1x}}=\lim{\frac{\frac1x}{-\frac{1}{x^2}}}=\lim{-x}=0$

De ha mondjuk azt tanultátok, vagy tudod bizonyítani, hogy n $\to$ $\infty$ esetén $\lim{\root{n}\of{n}}=1$ , akkor abból is könnyen kijön.

Előzmény: [1390] Khesteg, 2010-10-02 18:27:18

[1390] Khesteg	2010-10-02 18:27:18
Hát ebből nekem nem jön ki mert a határérték végig 0/0 alakú marad, mert nem tűnik el a nevezőből az x.

[1389] Csimby	2010-10-02 17:38:40
$x^x=(e^{\ln{x}})^x=e^{x\ln{x}}=e^{\frac{\ln{x}}{\frac{1}{x}}}$ és a kitevőre alkalmazhatod a L'Hospital-t.
Előzmény: [1388] Khesteg, 2010-10-02 17:11:55

[1388] Khesteg	2010-10-02 17:11:55
Valaki le tudná nekem vezetni a lim(x tart 0-hoz) x(az x-ediken) megoldását plz? Nem igazán tudom összehozni olyan alakra hogy alkalmazhassam a L'Hospital szabályt...vagy az nem is kell?

[1387] Maga Péter

2010-09-23 11:33:26

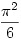Nem egészen. A wikipedia azt mondja, hogy $\zeta$ (2)-ről Euler 1735-ben mutatta meg, hogy $\frac{\pi^2}{6}$ , de a $\pi$ ²-ről csak 1794-ben bizonyította be Legendre, hogy irracionális. Euler pedig 1783-ban meghalt.

Valójában Euler bizonyítása (arra, hogy végtelen sok prím van) úgy nézett ki, hogy a

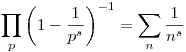
$\prod_p\left(1-\frac{1}{p^s}\right)^{-1}=\sum_n\frac{1}{n^s}$

s>1 feltétel mellett fennálló azonosságban tartott s-sel 1-hez. Ha pedig indirekte véges sok prím lenne, akkor a szorzat egy véges számhoz, az összeg pedig a végtelenbe tartana.

Előzmény: [1386] bily71, 2010-09-23 09:27:08

[1386] bily71

2010-09-23 09:27:08

Köszönöm, ez tetszik, zseniálisan egyszerü, elegáns és frappáns. Máris adtál egy ötletet. :)

Ez Eulertől származik, úgy-e?

Előzmény: [1374] Róbert Gida, 2010-09-21 20:04:59

[1385] bily71	2010-09-23 09:23:50
Vagyis nem a valódi kezdőlépés.
Előzmény: [1384] bily71, 2010-09-23 09:13:30

[1384] bily71	2010-09-23 09:13:30
Abban az értelemben közelebb jutnánk, hogy kizárjuk az első esetet, miszerint az ikerprimek száma véges, de ez nem a kezdő lépés a bizonyitás menetében.
Előzmény: [1383] Maga Péter, 2010-09-22 22:23:31

[1383] Maga Péter

2010-09-22 22:23:31

Azt mondod [1372]-ben, hogy ,,Én nem azt mondom, hogy közelebb kerülnénk a Brun-konstans problémájának megoldásához (...)''

Vesd már ezt össze a [1367]-es hozzászólásoddal: ,,"Az ikerprímsejtés bebizonyításával semmivel nem jutsz közelebb Brunhoz..."'' (ezt RG [1366]-osából idézed)

,,De igen!''

Most akkor mi van???

Előzmény: [1372] bily71, 2010-09-21 17:21:48

[1382] SAMBUCA	2010-09-22 17:02:11
nem véges, hanem véges tizedestört (alakú számok). minden [0,1]-beli szám véges.
Előzmény: [1381] bily71, 2010-09-22 16:35:02

[1381] bily71	2010-09-22 16:35:02
Igen. A csúcsok véges számokat reprezentálnak.
Előzmény: [1379] SAMBUCA, 2010-09-22 13:28:46

[1380] Tóbi	2010-09-22 13:34:23
Helyesek a meglátásaid.
Előzmény: [1379] SAMBUCA, 2010-09-22 13:28:46

[1379] SAMBUCA	2010-09-22 13:28:46
(i) hibás. nem egy csúcs reprezentál egy valós számot, hanem egy (végtelen hosszú) út.
Előzmény: [1377] bily71, 2010-09-22 12:38:37

[1378] bily71	2010-09-22 12:41:48
A csúcsok helyett számolhatjuk az éleket is, hiszen minden élhez rendelhető egy valós szám.
Előzmény: [1377] bily71, 2010-09-22 12:38:37

[1377] bily71

2010-09-22 12:38:37

Tehát mégegyszer:

(i) a fában ugyanannyi elágazás (csúcs) van, mint valós szám,

(ii) a szintek száma megszámlálhatóan végtelen,

(iii) minden szinten véges sok elágazás van, (az n-edik szinten 10ⁿ darab),

(iv) alkossanak az egy szinten lévő elágazások halmazokat,

(v) megszámlálhatóan végtelen sok véges elemszámú halmaz uniója megszámlálhatóan végtelen sok elemü halmazt eredményez.

Hol a hiba?

Előzmény: [1373] bily71, 2010-09-21 17:47:53

[1376] bily71	2010-09-22 12:18:54
Olvasd el az [1357]-t, az [1362]-t s és az [1365]-t.
Előzmény: [1375] Nánási József, 2010-09-21 20:06:29

[1375] Nánási József	2010-09-21 20:06:29
Kedves bily71! Kérlek írd fel nekem $\frac13$ -ot kétféle tizedestört alakban.
Előzmény: [1353] bily71, 2010-09-20 19:25:18

[1374] Róbert Gida

2010-09-21 20:04:59

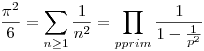
$\frac {\pi ^2}{6}=\sum _{n\ge 1}\frac {1}{n^2}=\prod _{p prim} \frac {1}{1-\frac {1}{p^2}}$

Bal oldalt irracionális szám áll, így nem lehet véges sok prím, mert különben a jobboldalt racionális szám állna. Ez klasszikus bizonyítás, de Erdőstől is van egy ilyen bizonyítás.

Előzmény: [1372] bily71, 2010-09-21 17:21:48

[1373] bily71

2010-09-21 17:47:53

"Sirpi módszerrel" megszámlálható, ugyanis minden elágazásnál tizszeresre nő a bejárható utak száma, mivel n elágazás van (n= $\infty$ ), az utak száma 10ⁿ.

1/2 másodperc alatt elszámolok 1-ig, 1/4 alatt 10-ig, 1/8 alatt 100-ig, és igy tovább, vagyis 1 mp. alatt megszámoltam az összes utat :-)

Előzmény: [1353] bily71, 2010-09-20 19:25:18

[1372] bily71

2010-09-21 17:21:48

Mondanál egy példát arra, hogy úgy sikerült bizonyitani valamely természetes számokból álló sorozat végtelen voltát, hogy a tagok reciprokainak részösszegének sorozata irracionális számhoz tart? Egyátalán, hogy lehetünk ebben biztosak, mig nem tudjuk, hogy véges-e, vagy végtelen? (Egy rac. szám lehet két nagyon-nagyon nagy egész szám hányadosa is.)

Én nem azt mondom, hogy közelebb kerülnénk a Brun-konstans problémájának megoldásához, hanem azt, hogy ha tisztáztuk az ikerprim-kérdést, akkor elkezdhetjük a vizsgálódást, addig nem. Ha tévedek, légy szives javits ki, de ne úgy, hogy: "nincs igazad".

Előzmény: [1368] Maga Péter, 2010-09-21 11:36:43

[1371] Maga Péter	2010-09-21 11:56:35
Még egy érdekesség: van olyan végtelen játék, ahol egyik félnek sincs nyerő stratégiája, ami egy kicsit furcsa a véges játékokhoz szokott szemnek. Ennek bizonyítása a kiválasztási axiómán múlik. Ez az egyik szép példája annak, hogy a kiválasztási axióma -- hasson bármily természetesnek -- elég erős, nagyon-nagyon nem természetesnek ható következményekkel bír.
Előzmény: [1370] Maga Péter, 2010-09-21 11:52:51

Már regisztráltál?
Új vendég vagy?