Fórum: Valaki mondja meg!

Lehet, hogy van egyszerűbb megoldás, csak én vagyok fáradt hozzá.

köszönöm a segítséget. triviális feladatok között volt, és miután gondoltam/ajánlották a szitára/a szitát, én még mindig azt hittem, van valami teljesen nyilvánvaló megoldás, amit nem veszek észre.

Nem, ez így hibás, mert a mazsolák eloszlkása nem ugyanaz, mint a pálcikák eloszlása. Például ha két mazsolád és két süteményed lenne, akkor 1/4 valószínűséggel menne a bal oldali süteménybe mindkét mazsola, de 1/3 valószínűséggel menne mindkét mazsola a pálcáktól balra.

Feltételezem, hogy ezt úgy kell érteni, hogy ha a nagymama az egész tésztába rakott mazsolákat pontosan leszámolja, és biztosan ugyanannyit, n darabot rak.

Ha a tésztát tíz részre osztja, akkor minden mazsola egymástól függetlenül kerül a tíz rész valamelyikébe, és feltesszük azt is, hogy a tíz rész pontosan egyforma méretű, vagyis egyforma valószínűséggel kerülnek beléjük a mazsolák.

Most akkor ha kiválasztassz k konkrét süteményt, akkor annak a valószínűsége, hogy az összes mazsola ezekbe kerül, (k/10)ⁿ. Ebből azt hiszem, szitával következik, hogy annak a valószínűsége, hogy minden süteménybe kerül mazsola,

Ezt átalakítod 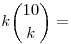alapján, majd az összeget explicit alakra hozod, és innen próbáld meg te megoldani.

igen ez megvolt, de még mindig nem teljesen világos. lerakunk egy sorba n golyót, és lerakunk közéjük 9 pálcikát. és ahogy sorban rakosgatjuk a pálcikákat, mindig megnézzük, hogy mekkora valószínűséggel kerül olyan helyre (pl két pálcika egymás mellé), hogy az egy süteményre 0 mazsolát eredményezne. ez így megállja a helyét? most mondhatnám hogy azért csináltam golyókkal-pálcikákkal mert egy nem szakkörös gimisnek kell elmagyaráznom (egyébként így van), de igazából azért azért, mert nem tudtam kitalálni semmilyen matematikai képletes vagyis klasszikus megoldást.

Ha n tárgyat elhelyezünk 10 dobozban véletlenszerűen, mennyi a valószínűsége, hogy nem lesz üres doboz?

Egy másik lehetőség, hogy megkérdezzük a nagymamát.

Az első feladatban az egyenlet sinx-re másodfokú. Ha gondolod sinx-et jelölheted pl.: a-val. A-t beírva a sinx helyére egy sima másodfokú egyenletet kapunk.(öt a négyzet mínusz három a mínusz egy egyenlő nulla). Ezt gondolom meg tudod oldani. Lesz két megoldás, ebből jelen eseteben egy lesz mínusz egy és egy közötti. A színusz ÉK-e -1 - 1, tehát a másodfokú egyenlet egyik megoldásából (amelyik nem esik mínusz egy és egy közé) nem lesz megoldás, a másikból pedig teljesen egyszerűen sinx=a, amit gondolom szintén meg tudsz oldani. A második egyenletet átalakíthatod úgy, hogy 9sinx négyzet-(sinx négyzet+cosx négyzet)=8, ebből a négyzetes összefüggést használva (sinx négyzet+cosx négyzet=1)sinx=1, innen már gondolom megy. És most sajnos el kell mennem...

Sziasztok! Nem tudom megcsinálni a következő feladatot, elvileg könnyű, de mégsem tudom elkezdeni sem. Szóval egy nagymama süteményt süt, 1 kg tésztát gyúr össze, amibe mazsolát is tesz. Utána a tésztát 10 részre osztja, és ezek lesznek a sütemények. Hány mazsolát kell belegyúrnia a tésztába, hogy legalább 99 százalékos valószínűséggel mindegyik darabba jusson legalább 1 db mazsola?

Sziasztok ! Tud valaki segíteni SOS Ezeket a feladatokat kellene megoldanom!

5 sin 2-on x-3sin x=1

8 sin 2-on x -cos 2-onx=8

tg x +ctg x=2

Lécci magyaráűzzátok el hogy kell megcsinálni !!

Köszi!!

...Köszönöm szépen a ,,támogató" hozzáállást '

Jogos, tényleg kissé durvára sikerült a reakció (amire Te meg is találtad az ütős választ - azért remélem, egy hsz alapján nem leszek egy polcra pakolva RG-vel :-) ). Csak ezek a dolgok már lényegében ki lettek tárgyalva a Goldbach-os topikban, és próbáltam elejét venni, hogy ide is átköltözzenek.

Na, kezdesz hasonlitani robert gidára stilusban :)

Amugy ha valaki neki akar állni komoly sejtéseknek vagy nehezebb feladatoknak érdemes előbb tisztába lenni pontosan a logikával (meg persze még...-al), de hogy miből mi következik, például látszik, hogy amire itt akartál ( ez most nem sirpinek szolxd) utalgatni, azok önmagukban igazak, sőt trivik voltak, de te ugy láttad vmiért hogy következik belőle a goldbach sejtés, (vaaagy lehet hogy csak ki akartál jönni néhány trivi állítással, ami véletlenül olyan goldbach sejtéses volt :))

Szóval probálkozz előbb egyszerűbb dolgokkal szépen lépésről lépsre begyakorolni a következtetési szabályokat, na sok sikert.

Légyszi csak egy topikot szemetelj tele a Goldbach-sejtéssel kapcsolatban, szóval ezt például ne. Előre is köszi.

Egyébként sikerült belátnod, hogy minden páros szám előáll két páratlan összegeként, grat.

Tisztelt fórumozók ! Kérem igazolják vagy cáfolják az alábbi állításaimat : 1. minden 2-nél nagyobb prím felírható 2n+1 formájában , 2. minden páros szám felírható 2n alakban , 3. ha p és k prímeket felírjuk : p=2n+1 és k=2z+1 akkor p+k=(2n+1)+(2z+1) -esetleg ez egyenlő továbbá 2(n+z+1) -el ??? 4. minden 2-nél nagyobb szám felírható,mint két szám összege +1 vagyis,ha x nagyobb,mint 2 akkor x felírható,mint x=a+b+1 Segítségüket előre is köszönöm szépen !

Egyszerű kulcsszavakra kereséssel itt egy link például.

Üdv! Az érdekelne, hogyan lehet sorok összegét komplex függvények segítségével (rezidum tétel alkalmazásával) kiszámolni. Egy konkrét kidolgozott példa is jól jönne. Sajnos erről nem nagyon találok anyagot:S Előre is köszönöm!

Az akinek van olyan gépe, amivel numerikusan ki tudja integrálni, akár ki is dobhatja ezeket a táblázatokat, feltéve, hogy a gépe nem 3V-os gombbelemmel működik, ami ha esetleg lemerülne nem kapható a közelben lévő éjjel nappal nyitva tartó FICKO áruházban. Ilyenkor aztán lehetséges, hogy arra fog kényszerülni, hogy a szemétből előkeresse a kidobott táblázatokat, ha véletlenül nem környezetvédő és nem vitte el már korábban a legközelebbi szelektív hulladékgyűjtőbe. Ekkor persze letölthetné a Netről, de ha javaslatodnak megfelelően onnan is kidobták ezeket, akkor arra kényszerül, hogy elmenjen és kihalássza a szelektív gyűjtőből, azt remélve, hogy azóta nem ürítették ki a tartályt. Ha véletlenül kiürítették, akkor még mindig bízhat abban, hogy van a Földön olyan ember, aki csupán heccből betanulta az egész Fi(z) táblázatot. Gondolva arra, hogy a Föld mágneses terének csökkenésével egy esetleges nagyobb napkitörés az egész földi számítógépes rendszert tönkre teszi.

Már, ha benne van a táblázatban, egyébként meg interpolálni kell a két szomszédos értékből.

Vagy géppel numerikusan kiintegrálni, és akkor ezeket a táblázatokat ki is dobhatjuk.

Bocsánat ! ... igen valóban ,... a kérdés pedig az lenne HOGY bizonyítjuk be , hogy ebben az esetben n bármely értékére létezik egy k és egy p ,,különböző" szám mire az egyenlet igaz !

Igen ! igaz ! KÖSZÖNÖM SZÉPEN !!! ... Bocsánat,csak azt ki hagytam,hogy k nem lehet egyenlő p-vel ! BOCSÁNAT !!!

Nem, ez elméletileg sem igaz. Egy azonosság bizonyítása azt jelenti, hogy kimutatjuk: a felírt egyenlőség a benne szereplő változók bármely megengedett értéke mellett teljesül. A szóban forgó egyenlőség pl n=2, p=0 és k=0 esetben nem igaz, tehát van ellenpélda. Persze végtelen sok ellenpélda van ... de ha csak egyetlen is akad, akkor már nincs mit bizonyítani.

Megpróbálok segíteni, hogy a „feladat koncepcionálisan összeálljon a fejedben”.

Teljes táblázat: itt

Köszönöm ! ...,de így akadtam rá ! ... és elméletileg ez igaz is ,mert ,ha n=2,p=0,k=1 ebben az esetben az ,,állítás" igaz ... és így tovább. szóval csak egy bizonyítás levezetését lehet-e erre ,,csinálni" ??? KÖSZÖNÖM SZÉPEN !

Humbug lenne.

Nem is igaz (általában ...), hogy az "adataiddal" n = k+p+1.

Biztosan így akartad feltenni a kérdést / biztosan ez a feladat?

Tisztelt Fórumozók ! SEGÍTSETEK !!! KÖSZÖNÖM !

Ha n=2,3,4,5,...,+végtelenig, p=0,1,2,...,+végtelenig és k=0,1,2,...,+végtelenig akkor az n=k+p+1 bizonyítása mi lenne ?