|
| [1536] Kemény Legény | 2011-05-26 14:00:11 |
 Észrevétel:
a0b2+a1b+a2=(a0b+a1)b+a2
a0b3+a1b2+a2b+a3=((a0b+a1)b+a2)b+a3
a0b4+a1b3+a2b2+a3b+a4=(((a0b+a1)b+a2)b+a3)b+a4
a0b5+a1b4+a2b3+a3b2+a4b+a5=((((a0b+a1)b+a2)b+a3)b+a4)b+a5
Ez alapján néhány egyszerű lépéssel hozd pl. felső háromszögmátrix alakra.
|
| Előzmény: [1535] komalboy, 2011-05-26 13:40:11 |
|
| [1535] komalboy | 2011-05-26 13:40:11 |
 Sziasztok!
Valaki gyorsan (a héten) tudna szép megoldást - bizonyítást - adni a következő problémára?
Előre is köszi. :)
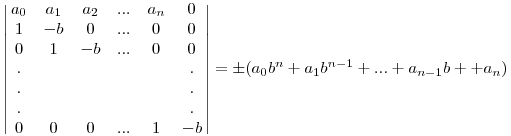
|
|
| [1534] pvong17 | 2011-05-26 01:33:41 |
 A divergenciáról és a rotációról tudtok valahol érthető leírást?
|
|
|
| [1532] Valvehead | 2011-05-16 21:38:19 |
 Egy diff. egyenletet megoldottam és még a powerful wolfram mathematica segítségével sem vagyok biztos benne, hogy jó-e? A könyvben máshogy van, ezért érdekel nagyon, hogy jól csináltam-e. Ha nem, akkor hol hibáztam? A feladat: Y'=(x+7y+2)/(3x+5y+6)
Először eltüntetem a konstansokat: u=x-2; v=y; du=dx; dv=dy Így az egyenlet: 1. dv/du=(u+7v)/(3u+5v)
A z=v/u helyettesítés szétválasztható diff. egyenletre vezet, kérdés, mi lesz a dv/du?
Nálam: z=(v/u) => dz/dv=1/u => dv=dz*u; Ezt visszaírva az 1. egyenletbe:
(dz*u)/du=(1+7z)/(3+5z)
Legjobb tudásom szerint helyesen jártam el, de a könyvben nagyon más megoldás van, mint amit én kapok. Köszönöm szépen előre is annak, aki segít!
|
|
|
| [1530] Füge | 2011-05-11 20:29:59 |
 Szia!
Az érintős feladatoknál (ha nem akarunk deriválni) azt kell kihasználni, hogy az érintőnek és az adott alakzatnak pontosan egy metszéspontja van, azaz ha megoldjuk a két egyenletet egyenletrendszerként, akkor annak pontosan egy megoldása lesz.
Legyen az egyenes egyenlete: e: y=mx+b
k: x2+y2=16
p: 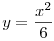
Nézzük meg először az egyenes és a kör metszéspontját. Helyettesítéssel a következő egyenletet kapjuk:
x2+(mx+b)2=16
x2+m2x2+2mbx+b2=16
x2(1+m2)+x(2mb)+(b2-16)=0
Egy másodfokú egyenletnek akkor és csak akkor van pontosan egy megoldása, ha a diszkriminánsa 0, tehát:
(2mb)2-4(1+m2)(b2-16)=0
Ebből 64m2-4b2+64=0
A parabola és az érintő egyenes metszéspontja:
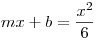
0=x2-(6m)x-6b
Az előzőek alapján D=0
36m2+24b=0
Innentől gondolom már megy, kétismeretlenes másodfokú egyenletrendszer.
|
| Előzmény: [1529] laci777, 2011-05-11 19:57:42 |
|
| [1529] laci777 | 2011-05-11 19:57:42 |
 Sziasztok!
A segítségeteket szeretném kérni egy E2-szintű példánál:( (ha lehet):
A feladat meghatározni az x2+y2=16 kör, és a 6y=x2 parabola közös érintőegyeneseinek egyenletét.
Sajnos csak addig világos, hogy y tengelyre szimmetrikus a 2 egyenes, de még deriválással sem megy, mivel az 1/3x máshol x, mint ahol a -x/négyzetgyök(16-x2) az x:( (ráadásul deriválás nélkül kellene megoldani).
Mentségem, hogy ilyen jellegű példát sem vettünk:(
Előre is köszönök szépen minden segítséget:)
Szép estét kívánok mindenkinek!
|
|
|
|
| [1526] jonas | 2011-05-07 22:50:42 |
 Amikor a fodrász vágja a hajamat, akkor leveszem a szemüvegemet, úgyhogy nem sokat látok. Ő viszont lát engem, akár közvetlenül, akár a tükörből, mert persze a fodrász szalonban tükör van a falon.
|
| Előzmény: [1521] Hajnika96, 2011-05-07 12:13:34 |
|
| [1525] lorantfy | 2011-05-07 20:43:32 |
 Periszkóppal nézel valakit egy fal mögül, aki a periszkóp csövét látja ugyan, de mivel a szemedet a periszkóp csövéhez szorítod, arról nagyon kevés fény indul visszafelé, így a másik ember a szemedet sem láthatja.
|
 |
| Előzmény: [1521] Hajnika96, 2011-05-07 12:13:34 |
|
|
|
| [1522] HoA | 2011-05-07 19:09:28 |
 Többféle lehetséges megoldás van. Én egy olyat mutatok, amihez tükör sem kell - de persze tükörrel is igaz marad. Ha valaki egy sötét szobában áll, ahonnan egy kis kémlelőnyíláson néz ki - pl. lakótelepi lakásajtókon van ilyen - ő lát téged, aki kint állsz de te nem látod őt - akár tükörrel csináljátok ezt akár közvetlenül.
|
| Előzmény: [1521] Hajnika96, 2011-05-07 12:13:34 |
|
| [1521] Hajnika96 | 2011-05-07 12:13:34 |
 Fizika órán kaptunk egy kérdést és ha azt hétfőre jól megválaszolom kapok egy ötöst. A kérdés a következő: Láthat-e tükörből bennünket az, akit mi nem látunk?Hogyan?
A segítséget előre is köszönöm:)
|
|
| [1520] Moderátor | 2011-04-24 19:26:44 |
 ,,Én láttam a feladatot, ezért nem is akartam először megnevezni a kérdezőnek, illetve többet mondani róla, viszont miután már feltöltötted a bizonyítását már lényegében mindegy volt.''
Egyáltalán nem volt mindegy.
Ilyen esetben az a teendő, hogy azonnal értesíted a szerkesztőséget és a moderátorokat.
|
| Előzmény: [1514] Zine, 2011-04-22 20:16:59 |
|
| [1519] Maga Péter | 2011-04-24 13:12:18 |
 És ha most valamelyik megoldás betűről betűre egyezik akár a Zine, akár az én postommal, akkor sem lehet tőle elvenni a pontokat, mert nem tudjátok eldönteni, hogy Radián-e az illető, vagy csak egy nyitott szemmel (és némi szerencsével) fórumozó versenyző.
|
| Előzmény: [1517] Moderátor, 2011-04-23 12:53:10 |
|
|
| [1517] Moderátor | 2011-04-23 12:53:10 |
 A moderátorok nincsenek olyan sokan, és nem vették észre. :-(
A [1484] a) kérdése a B.4345. feladathoz kapcsolódott. (Mondjuk R(3,3,3)=17 nem sokat segít a megoldáshoz.)
Elég nagy szemtelenség aktív kömal feladatokhoz épp a kömal fórumon segítséget kérni...
|
| Előzmény: [1511] Maga Péter, 2011-04-22 15:11:23 |
|
|
|
| [1514] Zine | 2011-04-22 20:16:59 |
 Én láttam a feladatot, ezért nem is akartam először megnevezni a kérdezőnek, illetve többet mondani róla, viszont miután már feltöltötted a bizonyítását már lényegében mindegy volt.
Egyébként ilyenkor, ha valaki ismeri a tételt, akkor leírja a megoldásában hogy ez a tétel neve, hivatkozik egy bizonyításra, és kész? Vagy erre nem is adnának pontot?
|
| Előzmény: [1511] Maga Péter, 2011-04-22 15:11:23 |
|
| [1513] rizsesz | 2011-04-22 18:49:20 |
 Ez azért meglehetősen furcsa; szerintem talán az történhetett, hogy az elektronikusan beküldött megoldások értékét feltöltötték, a papír alapúakat pedig még nem (ilyen olykor megesik).
|
| Előzmény: [1512] Róbert Gida, 2011-04-22 17:32:24 |
|











