Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Fórum: Valaki mondja meg!

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]    [79]    [80]    [81]    [82]    [83]    [84]    [85]    [86]    [87]    [88]    [89]    [90]    [91]    [92]    [93]  

Szeretnél hozzászólni? Jelentkezz be.
[1551] phoenix2011-10-04 18:11:47

Sziasztok, azt szeretném kérdezni, hogyha be kell látnunk, van két olyan prímszám, amely osztható 10 ad 10-nel, akkor bizonyításnak mondható, ha egy konkrét példát veszünk? (10 ad 10+3 ; 3) mondjuk fejből nem tudnék ilyet mondani, de ez is tipikus skatulyaelves megoldást igényel? skatulyáknak lehet venni a 10 ad 10-nel vett osztási maradékokat? és ha azt kell belátni hogy végtelen sok prímszám közül bármely kettő különbsége osztható 129-cel? Mondjuk 129 = 3*43... Köszönöm

[1550] Bütyök2011-09-18 18:51:52

Boldog boldogtalan blogolja a finoman szólva vízióit:) Legjobb csak a matematikai definiciókat figyelembe venni. Az pedig a differenciálgeometria tárgyalja. Ilyeneket nem olvasok el....

Előzmény: [1549] pvong17, 2011-09-10 02:31:44
[1549] pvong172011-09-10 02:31:44

Néhány hónapja a rotációról és a divergenciáról kérdeztem. itt van egy leírás róluk, ha még érdekel valakit: divergencia, rotáció.

Előzmény: [1534] pvong17, 2011-05-26 01:33:41
[1548] SmallPotato2011-08-09 23:14:47

"az indukcióvektor mindig merőleges a (pl. részecske) sebességére" - ez így nyilván nem igaz. Adott mágneses térbe például az indukcióvektor irányához képest bármilyen irányú sebességgel belőhetünk részecskét, és annak sebessége (irányban és nagyságban) nyilván nem ugrásszerűen fog változni.

A bevezető mondat eredetileg (és helyesen) bizonyára kb. úgy hangzik, hogy "a Lorentz-erő mindig merőleges a részecske sebességére" (és tegyük hozzá: az indukcióvektorra), amiből kiderül az is, hogy a szóban forgó erő nem az (akár álló, akár mozgó) mágnesezhető anyagokra, hanem a mágneses térben mozgó elektromos töltésekre hat.

Előzmény: [1547] mathbf, 2011-08-09 21:39:35
[1547] mathbf2011-08-09 21:39:35

A mágneses mező nem végez munkát, mivel az indukcióvektor mindig merőleges a (pl. részecske) sebességére. Ezt írja a tankönvem. Akkor azt, hogy két mágnes vonzza egymást, vagy a mágnes vonzza a vasreszeléket minek tudjuk be? A vasreszelék mozog miközben erő hat rá, tehát munkavégzés történik, nem?

[1546] epsilon2011-07-11 15:14:34

Köszi! Ez valóban így van!

Előzmény: [1545] sakkmath, 2011-07-10 17:49:52
[1545] sakkmath2011-07-10 17:49:52

Igaz. Korongok helyett gyalogokkal:

Előzmény: [1544] epsilon, 2011-07-10 16:37:01
[1544] epsilon2011-07-10 16:37:01

Üdv mindenkinek! Lenne egy kérdésem: igaz-e, hogy egy 8×8-as sakktáblán elhelyezhető 16 korong úgy, hogy minden sorban, minden oszlopban és a két átló mentén is 2-2 korong legyen? Előre is kösz a választ, üdv: epsilon

[1543] Csimby2011-06-19 20:26:06

Szerintem itt a legelső jegyzetben megtalálod: http://www.math.elte.hu/ mori/oraim.html

Előzmény: [1542] Fernando, 2011-06-19 13:48:28
[1542] Fernando2011-06-19 13:48:28

Egy statisztikai kérdésben kérem lehetőleg gyors segítségeteket. Kérdés: milyen regularitási feltételek esetén alkalmazható likelihood-hányados próba? (mikor tart eloszlásban a -2lnA chi négyzet eloszláshoz?) Milyen eloszlások esetén teljesülnek ezek a regularitási feltételek?

Köszi!

[1541] Zilberbach2011-05-28 15:16:11

Elnézést kérek, ha túl kereskedelmi jellegű a kérdésem, de lehet hogy mást is érdekelne a válasz.

A laptopomról kezd letörni a (fölhajtható) képernyő ezért azt fontolgatom, lehet hogy veszek egy tabletet, azzal nem fordulhat elő ilyen baleset.

Az árakat böngészve azt vettem észre hogy a windows-os tabletek általában kb. dupla áron vannak, mint az androidosok.

Mi az ami miatt ezt a jelentős árkülönbözet esetleg megérheti kifizetni a fölhasználónak?

[1540] farkasroka2011-05-27 06:10:40

jaaajjjjjj:)

köszi!!

Előzmény: [1539] Fálesz Mihály, 2011-05-26 19:48:10
[1539] Fálesz Mihály2011-05-26 19:48:10

Segítség: y\cdot y' = \left(\frac{y^2}2\right)'.

Előzmény: [1538] farkasroka, 2011-05-26 18:42:21
[1538] farkasroka2011-05-26 18:42:21

Sziasztok!

Van egy diffegyenletem, konkrétan az alábbi.

Csak azt szeretném tudni, hogy néz ki az általános megoldása. (pl. lineáris inhomogénnél C1Y+C2Y+y0) Elég lenne annyi, hogy hol nézzek utána. Eddig nem találtam semmit csak a lineáris esetről, azzal nincs is probléma.

Előre is köszi!

[1537] SAMBUCA2011-05-26 15:43:04

Én pedig azt javaslom, hogy keress nemnulla kifejtési tagokat, például az alapján, hogy az első sorból melyik elemet választottuk ki. nem lesz sok.

Előzmény: [1535] komalboy, 2011-05-26 13:40:11
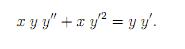[1536] Kemény Legény2011-05-26 14:00:11

Észrevétel:

a0b2+a1b+a2=(a0b+a1)b+a2

a0b3+a1b2+a2b+a3=((a0b+a1)b+a2)b+a3

a0b4+a1b3+a2b2+a3b+a4=(((a0b+a1)b+a2)b+a3)b+a4

a0b5+a1b4+a2b3+a3b2+a4b+a5=((((a0b+a1)b+a2)b+a3)b+a4)b+a5

Ez alapján néhány egyszerű lépéssel hozd pl. felső háromszögmátrix alakra.

Előzmény: [1535] komalboy, 2011-05-26 13:40:11
[1535] komalboy2011-05-26 13:40:11

Sziasztok!

Valaki gyorsan (a héten) tudna szép megoldást - bizonyítást - adni a következő problémára?

Előre is köszi. :)

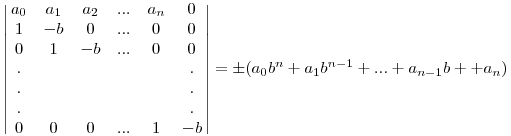
\left|\matrix{a_{0}&a_{1}&a_{2}&...&a_{n}&0\cr 1&-b&0&...&0&0\cr 0&1&-b&...&0&0\cr .&&&&&.\cr.&&&&&.\cr.&&&&&.\cr 0&0&0&...&1&-b\cr}\right| =\pm(a_{0}b^{n} + a_{1}b^{n-1} + ... + a_{n-1}b + + a_{n})

[1534] pvong172011-05-26 01:33:41

A divergenciáról és a rotációról tudtok valahol érthető leírást?

[1533] Valvehead2011-05-16 22:34:44

Jáájjj, de buta vagyok. Rájöttem, az előző bejegyzés mostmár tárgytalan.

Előzmény: [1532] Valvehead, 2011-05-16 21:38:19
[1532] Valvehead2011-05-16 21:38:19

Egy diff. egyenletet megoldottam és még a powerful wolfram mathematica segítségével sem vagyok biztos benne, hogy jó-e? A könyvben máshogy van, ezért érdekel nagyon, hogy jól csináltam-e. Ha nem, akkor hol hibáztam? A feladat: Y'=(x+7y+2)/(3x+5y+6)

Először eltüntetem a konstansokat: u=x-2; v=y; du=dx; dv=dy Így az egyenlet: 1. dv/du=(u+7v)/(3u+5v)

A z=v/u helyettesítés szétválasztható diff. egyenletre vezet, kérdés, mi lesz a dv/du?

Nálam: z=(v/u) => dz/dv=1/u => dv=dz*u; Ezt visszaírva az 1. egyenletbe:

(dz*u)/du=(1+7z)/(3+5z)

Legjobb tudásom szerint helyesen jártam el, de a könyvben nagyon más megoldás van, mint amit én kapok. Köszönöm szépen előre is annak, aki segít!

[1531] laci7772011-05-12 16:56:06

Kedves Füge!

Köszönöm szépen az érthetően adott magyarázatot és megoldást:)

További szép napot Neked - és mindenkinek:)

Előzmény: [1530] Füge, 2011-05-11 20:29:59
[1530] Füge2011-05-11 20:29:59

Szia!

Az érintős feladatoknál (ha nem akarunk deriválni) azt kell kihasználni, hogy az érintőnek és az adott alakzatnak pontosan egy metszéspontja van, azaz ha megoldjuk a két egyenletet egyenletrendszerként, akkor annak pontosan egy megoldása lesz.

Legyen az egyenes egyenlete: e: y=mx+b

k: x2+y2=16

p: 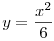y=\frac{x^2}{6}

Nézzük meg először az egyenes és a kör metszéspontját. Helyettesítéssel a következő egyenletet kapjuk:

x2+(mx+b)2=16

x2+m2x2+2mbx+b2=16

x2(1+m2)+x(2mb)+(b2-16)=0

Egy másodfokú egyenletnek akkor és csak akkor van pontosan egy megoldása, ha a diszkriminánsa 0, tehát:

(2mb)2-4(1+m2)(b2-16)=0

Ebből 64m2-4b2+64=0

A parabola és az érintő egyenes metszéspontja:

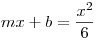
mx+b=\frac{x^2}{6}

0=x2-(6m)x-6b

Az előzőek alapján D=0

36m2+24b=0

Innentől gondolom már megy, kétismeretlenes másodfokú egyenletrendszer.

Előzmény: [1529] laci777, 2011-05-11 19:57:42
[1529] laci7772011-05-11 19:57:42

Sziasztok!

A segítségeteket szeretném kérni egy E2-szintű példánál:( (ha lehet):

A feladat meghatározni az x2+y2=16 kör, és a 6y=x2 parabola közös érintőegyeneseinek egyenletét.

Sajnos csak addig világos, hogy y tengelyre szimmetrikus a 2 egyenes, de még deriválással sem megy, mivel az 1/3x máshol x, mint ahol a -x/négyzetgyök(16-x2) az x:( (ráadásul deriválás nélkül kellene megoldani).

Mentségem, hogy ilyen jellegű példát sem vettünk:(

Előre is köszönök szépen minden segítséget:)

Szép estét kívánok mindenkinek!

[1528] Róbert Gida2011-05-11 01:57:30

Újra felfedezte a Ramsey tételt a kitűző? http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=B4345&l=hu

Előzmény: [1518] Róbert Gida, 2011-04-23 14:45:41
[1527] Hajnika962011-05-08 17:39:14

Köszönöm a segítséget!!:)

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]    [79]    [80]    [81]    [82]    [83]    [84]    [85]    [86]    [87]    [88]    [89]    [90]    [91]    [92]    [93]