|
| [1553] phoenix | 2011-10-04 19:59:49 |
 Nem tudom bebizonyítani, hogy prím, mert ha be tudnám, akkor onnan triviális lenne .. de nem hiszem hogy ilyen úton kell elindulni, azt kell bebizonyítani hogy van két ilyen prím, és az volt a kérdésem, hogy a bizonyítás ebben a részfeladatban ha mondok kettő ilyet az elég? vagy
|
| Előzmény: [1552] jonas, 2011-10-04 19:29:41 |
|
| [1552] jonas | 2011-10-04 19:29:41 |
 Nem értem. Azt szeretnéd belátni, hogy van két olyan prímszám, aminek a különbsége pontosan 1010 ? Be tudod bizonyítani, hogy mondjuk a 1010+33 prímszám, de a 1010+13 nem az?
|
| Előzmény: [1551] phoenix, 2011-10-04 18:11:47 |
|
| [1551] phoenix | 2011-10-04 18:11:47 |
 Sziasztok, azt szeretném kérdezni, hogyha be kell látnunk, van két olyan prímszám, amely osztható 10 ad 10-nel, akkor bizonyításnak mondható, ha egy konkrét példát veszünk? (10 ad 10+3 ; 3) mondjuk fejből nem tudnék ilyet mondani, de ez is tipikus skatulyaelves megoldást igényel? skatulyáknak lehet venni a 10 ad 10-nel vett osztási maradékokat? és ha azt kell belátni hogy végtelen sok prímszám közül bármely kettő különbsége osztható 129-cel? Mondjuk 129 = 3*43... Köszönöm
|
|
| [1550] Bütyök | 2011-09-18 18:51:52 |
 Boldog boldogtalan blogolja a finoman szólva vízióit:) Legjobb csak a matematikai definiciókat figyelembe venni. Az pedig a differenciálgeometria tárgyalja. Ilyeneket nem olvasok el....
|
| Előzmény: [1549] pvong17, 2011-09-10 02:31:44 |
|
|
| [1548] SmallPotato | 2011-08-09 23:14:47 |
 "az indukcióvektor mindig merőleges a (pl. részecske) sebességére" - ez így nyilván nem igaz. Adott mágneses térbe például az indukcióvektor irányához képest bármilyen irányú sebességgel belőhetünk részecskét, és annak sebessége (irányban és nagyságban) nyilván nem ugrásszerűen fog változni.
A bevezető mondat eredetileg (és helyesen) bizonyára kb. úgy hangzik, hogy "a Lorentz-erő mindig merőleges a részecske sebességére" (és tegyük hozzá: az indukcióvektorra), amiből kiderül az is, hogy a szóban forgó erő nem az (akár álló, akár mozgó) mágnesezhető anyagokra, hanem a mágneses térben mozgó elektromos töltésekre hat.
|
| Előzmény: [1547] mathbf, 2011-08-09 21:39:35 |
|
| [1547] mathbf | 2011-08-09 21:39:35 |
 A mágneses mező nem végez munkát, mivel az indukcióvektor mindig merőleges a (pl. részecske) sebességére. Ezt írja a tankönvem. Akkor azt, hogy két mágnes vonzza egymást, vagy a mágnes vonzza a vasreszeléket minek tudjuk be? A vasreszelék mozog miközben erő hat rá, tehát munkavégzés történik, nem?
|
|
|
|
| [1544] epsilon | 2011-07-10 16:37:01 |
 Üdv mindenkinek! Lenne egy kérdésem: igaz-e, hogy egy 8×8-as sakktáblán elhelyezhető 16 korong úgy, hogy minden sorban, minden oszlopban és a két átló mentén is 2-2 korong legyen? Előre is kösz a választ, üdv: epsilon
|
|
|
| [1542] Fernando | 2011-06-19 13:48:28 |
 Egy statisztikai kérdésben kérem lehetőleg gyors segítségeteket. Kérdés: milyen regularitási feltételek esetén alkalmazható likelihood-hányados próba? (mikor tart eloszlásban a -2lnA chi négyzet eloszláshoz?) Milyen eloszlások esetén teljesülnek ezek a regularitási feltételek?
Köszi!
|
|
| [1541] Zilberbach | 2011-05-28 15:16:11 |
 Elnézést kérek, ha túl kereskedelmi jellegű a kérdésem, de lehet hogy mást is érdekelne a válasz.
A laptopomról kezd letörni a (fölhajtható) képernyő ezért azt fontolgatom, lehet hogy veszek egy tabletet, azzal nem fordulhat elő ilyen baleset.
Az árakat böngészve azt vettem észre hogy a windows-os tabletek általában kb. dupla áron vannak, mint az androidosok.
Mi az ami miatt ezt a jelentős árkülönbözet esetleg megérheti kifizetni a fölhasználónak?
|
|
|
|
| [1538] farkasroka | 2011-05-26 18:42:21 |
 Sziasztok!
Van egy diffegyenletem, konkrétan az alábbi.
Csak azt szeretném tudni, hogy néz ki az általános megoldása. (pl. lineáris inhomogénnél C1Y+C2Y+y0) Elég lenne annyi, hogy hol nézzek utána. Eddig nem találtam semmit csak a lineáris esetről, azzal nincs is probléma.
Előre is köszi!
|
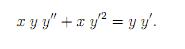 |
|
|
| [1536] Kemény Legény | 2011-05-26 14:00:11 |
 Észrevétel:
a0b2+a1b+a2=(a0b+a1)b+a2
a0b3+a1b2+a2b+a3=((a0b+a1)b+a2)b+a3
a0b4+a1b3+a2b2+a3b+a4=(((a0b+a1)b+a2)b+a3)b+a4
a0b5+a1b4+a2b3+a3b2+a4b+a5=((((a0b+a1)b+a2)b+a3)b+a4)b+a5
Ez alapján néhány egyszerű lépéssel hozd pl. felső háromszögmátrix alakra.
|
| Előzmény: [1535] komalboy, 2011-05-26 13:40:11 |
|
| [1535] komalboy | 2011-05-26 13:40:11 |
 Sziasztok!
Valaki gyorsan (a héten) tudna szép megoldást - bizonyítást - adni a következő problémára?
Előre is köszi. :)
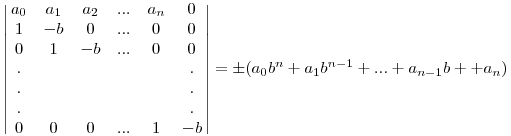
|
|
| [1534] pvong17 | 2011-05-26 01:33:41 |
 A divergenciáról és a rotációról tudtok valahol érthető leírást?
|
|
|
| [1532] Valvehead | 2011-05-16 21:38:19 |
 Egy diff. egyenletet megoldottam és még a powerful wolfram mathematica segítségével sem vagyok biztos benne, hogy jó-e? A könyvben máshogy van, ezért érdekel nagyon, hogy jól csináltam-e. Ha nem, akkor hol hibáztam? A feladat: Y'=(x+7y+2)/(3x+5y+6)
Először eltüntetem a konstansokat: u=x-2; v=y; du=dx; dv=dy Így az egyenlet: 1. dv/du=(u+7v)/(3u+5v)
A z=v/u helyettesítés szétválasztható diff. egyenletre vezet, kérdés, mi lesz a dv/du?
Nálam: z=(v/u) => dz/dv=1/u => dv=dz*u; Ezt visszaírva az 1. egyenletbe:
(dz*u)/du=(1+7z)/(3+5z)
Legjobb tudásom szerint helyesen jártam el, de a könyvben nagyon más megoldás van, mint amit én kapok. Köszönöm szépen előre is annak, aki segít!
|
|
|
| [1530] Füge | 2011-05-11 20:29:59 |
 Szia!
Az érintős feladatoknál (ha nem akarunk deriválni) azt kell kihasználni, hogy az érintőnek és az adott alakzatnak pontosan egy metszéspontja van, azaz ha megoldjuk a két egyenletet egyenletrendszerként, akkor annak pontosan egy megoldása lesz.
Legyen az egyenes egyenlete: e: y=mx+b
k: x2+y2=16
p: 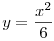
Nézzük meg először az egyenes és a kör metszéspontját. Helyettesítéssel a következő egyenletet kapjuk:
x2+(mx+b)2=16
x2+m2x2+2mbx+b2=16
x2(1+m2)+x(2mb)+(b2-16)=0
Egy másodfokú egyenletnek akkor és csak akkor van pontosan egy megoldása, ha a diszkriminánsa 0, tehát:
(2mb)2-4(1+m2)(b2-16)=0
Ebből 64m2-4b2+64=0
A parabola és az érintő egyenes metszéspontja:
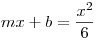
0=x2-(6m)x-6b
Az előzőek alapján D=0
36m2+24b=0
Innentől gondolom már megy, kétismeretlenes másodfokú egyenletrendszer.
|
| Előzmény: [1529] laci777, 2011-05-11 19:57:42 |
|