|
|
| [1590] Antal János Benjamin | 2011-12-29 14:31:08 |
 Elnézést, eléggé pontatlan vagyok. A feladat, hogy egy téglalap oldalai egész számok és területe és kerülete megegyezik, a két megoldás megvan, neten is kerestem rá megoldást, ott is csak a két megoldást láttam, konkrét levezetést sehol nem találtam. Tehát a és b is egész számok.
|
|
| [1589] takács krisztina | 2011-12-29 11:28:34 |
 Ha valai tud küldeni korábbi 9.-es Gordiusz feladatsorokat, annak nagyon örülnék, a takiri@freemail.hu címre kérem.
|
|
|
|
| [1586] Antal János Benjamin | 2011-12-29 02:16:29 |
 Sziasztok! Az alábbi egyenlőséget kéne megoldani (elvileg középiskolai emelt szintű matek tudással meg lehet ):
ab=2a+2b
Előre is köszönöm
|
|
|
|
| [1583] Lapis Máté Sámuel | 2011-12-10 15:51:11 |
 Sziasztok! Tudna valaki segíteni ebben a feladatban? A megoldás menetre is szükségem lenne!Mivel egyenlő 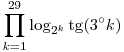 ? ?
|
|
|
| [1581] lorantfy | 2011-11-27 16:29:05 |
 Két pontból még nem tudod felírni a második parabola egyenletét. Kell még valamilyen információ. Jó lett volna, ha beírod az eredeti feladatot! Én arra gondolok, hogy a másik parabola szimmetria tengelye is az y tengely. Ha ez benne van az eredeti szövegben akkor BINGO! (Tudod honnan származik a BINGO szó?) Akkor csak egyetlen paramétert kell meghatározni, a-t. Mindkettőt toljad feljebb 10-el aztán integráljad őket -1-től +1 és a két integrál különbsége a közbezárt terület.
|
| Előzmény: [1580] laci777, 2011-11-27 15:56:42 |
|
| [1580] laci777 | 2011-11-27 15:56:42 |
 sziasztok!
tudna valaki segíteni az alábbi feladatban? meg kell(ene) határozni az y=3xnégyzet parabola, valamint az ezt az (1;3) pontban, az y tengelyt pedig a (0;-10) pontbam metsző másik parabola által bezárt terület nagyságát.
sajnos még a második parabolánál is annyit "sikerült" kiszámolnom, hogy (a+b)=13 (ahol az axnégyzet+bx-10 a második parabola egyenlete) onnan talán már menne(?)
előre is köszönöm szépen üdv laci
|
|
|
| [1578] Fálesz Mihály | 2011-11-22 06:55:05 |
 A különböző értelmben vett határértékeket nem lehet csak úgy össze-vissza cserélgetni (pedig időnként nagyon praktikus lenne). Itt legalább háromféle határérték keveredik össze, a végtelen szorzat, az egyes prímek kitevőinek összege, a különböző prímhatványok szintén végtelen szorzata... Tulajdonképpen végtelen sok divergens sorozat szorzatára próbálsz következtetni.
Ha a végtelen szorzat értéke egy pozitív racionális szám, akkor sem igaz, hogy egy prím kitevője a szorzatban (a részletszorzatok határértékében) egyenlő a tényezőkben szereplő kitevők összegével (a kitevők részletösszegei határértékével). Még akkor sem, ha a kitevők összege létezik.
Pl. lehet az összes ai tényező 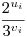 alakú, ahol ui,vi alkalmas pozitív egészek; ilyenek végtelen sorzataként minden nemnegatív szám előáll. (A alakú, ahol ui,vi alkalmas pozitív egészek; ilyenek végtelen sorzataként minden nemnegatív szám előáll. (A 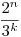 alakú számok a pozitív valós számok között sűrűn vannak.) alakú számok a pozitív valós számok között sűrűn vannak.)
De olyan végtelen szorzatot sem nehéz konstruálni, ahol az összes prím összesen kétszer szerepel, egyszer a számlálóban, egyszer a nevezőben, összességében minden prím ,,kiesik'', a szorzat értéke mégsem 1, hanem mondjuk 2.
|
| Előzmény: [1576] bily71, 2011-11-21 22:28:11 |
|
|
| [1576] bily71 | 2011-11-21 22:28:11 |
 Üdv!
Lenne egy kérdésem.
A pozitív racionális számok definíció szerint felírhatók két azonos előjelű egész hányadosaként. Az egyértelműség kedvéért vegyük csak azt az esetet, mikor mind a számláló, mind a nevező pozitív egész.
A számelmélet alaptétele szerint bármely egynél nagyobb pozitív egész, a sorrendtől eltekintve, egyértelműen bomlik prímszámok szorzatára. Ebből következik, hogy  n n N* felírható N* felírható 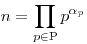 alakban, ahol P={prímek}, alakban, ahol P={prímek},  p p N és 0, vagy véges sok esetben igaz, hogy N és 0, vagy véges sok esetben igaz, hogy  p p 0. 0.
A fentiekből következik, hogy  q q Q+ felírható Q+ felírható 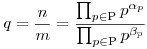 alakban, mely felírás egyértelmű, ahol n,m alakban, mely felírás egyértelmű, ahol n,m N*, (n,m)=1, N*, (n,m)=1,  p, p, p p N és 0, vagy véges sok esetben igaz, hogy N és 0, vagy véges sok esetben igaz, hogy  p, p, p p 0. 0.
Legyen (an,n N*) olyan sorozat, ahol ai N*) olyan sorozat, ahol ai Q+! Ekkor Q+! Ekkor 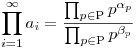 , mely alakot az egyszerűsítések elvégezte után kapunk. , mely alakot az egyszerűsítések elvégezte után kapunk.
A kérdésem:
Jól gondolom-e, hogy amennyiben az egyszerűsítések elvégezte után 0, vagy véges sok esetben igaz, hogy  p, p, p p 0, akkor 0, akkor 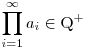 , különben , különben 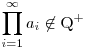 ? ?
Másik:
Jól gondolom-e, hogy ha létezik olyan prím, hogy a sorozat végtelen sok tagjára igaz, hogy a prím előfordul a nevezőben, de véges sok tagjára igaz, hogy előfordul a számlálóban, vagy fordítva, a sorozat végtelen sok tagjára igaz, hogy a prím előfordul a számlálóban, de véges sok tagjára igaz, hogy előfordul a nevezőben, akkor 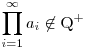 ? ?
|
|
|
| [1574] laci777 | 2011-10-17 15:45:56 |
 Sziasztok!
Ugyan most vesszük a deriválást, de egy feladat kifogott rajtam. Ha valaki tudna segíteni, megköszönném.
A példa: adott egy r sugarú gömb. Mekkora az ebbe a gömbbe szerkeszthető maximális térfogatú henger?
Bocs, ha túl egyszerű ez a pélfa, de bevallom kifog rajtam:(
Előre is köszönöm.
|
|
| [1573] Tóbi | 2011-10-15 18:16:03 |
 Legyen O egy pont a síkon. Legyen r az O távolságának maximuma az 5n adott objektumtól. Vegyünk egy O középpontú R sugarú kört. Ha R elég nagy, akkor belátjuk, hogy lesz rajta megfelelő P pont. A körvonal egy pontjának távolsága egy adott ponttól legalább R-r, ezen távolságok összege így legalább 2nR-2nr. Ha e egy adott egyenes, legyen e' a vele párhuzamos O-n átmenő egyenes. Ha p a körvonal egy pontja, akkor p és e távolsága legfeljebb annyi, mint p és e' távolsága plusz r. p és e' távolságának átlaga, miközben p fut a körön 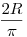 lesz, mivel ennyi a |sin(x)|R függvény átlagos nagysága is. Így összegezve a 3n egyenesre legfeljebb lesz, mivel ennyi a |sin(x)|R függvény átlagos nagysága is. Így összegezve a 3n egyenesre legfeljebb 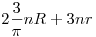 lesz az átlagos távolságösszeg. Ha R elég nagy, akkor lesz az átlagos távolságösszeg. Ha R elég nagy, akkor 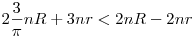 . Tehát valamely P pont jó lesz a körvonalon (például az, aminek minimális a távolságösszege az egyenesektől). . Tehát valamely P pont jó lesz a körvonalon (például az, aminek minimális a távolságösszege az egyenesektől).
|
| Előzmény: [1572] logarlécész, 2011-10-15 16:03:51 |
|
| [1572] logarlécész | 2011-10-15 16:03:51 |
 Adott a síkon 2n pont és 3n egyenes. Bizonyítsuk be, hogy van a síkon olyan P pont, hogy P-nek a 3n egyenestől való távolságainak összege kisebb, mint p-nek a 2n ponttól való távolságainak összege!
Eddig még n=1-re sem tudtam belátni.
Ha valaki tudna segíteni megköszönném. (Nem fontos és sürgős, csak érdekel.)
|
|
|
|
| [1569] phoenix | 2011-10-05 17:45:17 |
 Valamit én is gondoltam, de azt hittem átlátom amit írtam, de mégse ... lényegében az a) ill. b) feladatrész ugyanolyan elven működik ezek szerint, csak máshogy kell csoportosítani. Köszi a pontosítást vagy az érthetőbb megvilágítást :-) Köszi
|
| Előzmény: [1568] Sirpi, 2011-10-05 17:13:38 |
|
| [1568] Sirpi | 2011-10-05 17:13:38 |
 Uhh, belekavarodtam a skatulyáidba :-)
A lényeg, hogy 129 skatulyánk van (a prímek 129-es maradéka alapján), tehát valamelyik maradékból végtelen sok van, és erre a végtelen sok prímre igaz, hogy bármely kettő különbsége osztható 129-cel. Nyilván ez a bizonyítás tökéletesen működik bármilyen más számra is. Lényegében ezt írtad le Te is, csak túl sok volt a kérdőjel, és túl hosszúak a mondatok :-)
|
| Előzmény: [1567] phoenix, 2011-10-05 16:40:36 |
|








 Q+ esetén
Q+ esetén  p lehet végtelen is, sőt lehet, hogy nem is értelmezett. Előfordulhat, hogy
p lehet végtelen is, sőt lehet, hogy nem is értelmezett. Előfordulhat, hogy  n
n 0.
0.  p
p
