| [161] epsilon | 2007-02-28 19:26:43 |
 Hali! Szerintem nem létezik egy legnagyobb A mert a jobboldal bármilyen nagy lehet, ugyanis a jobboldali kifejezés így írható (n/n-1) az (n-1)-ik hatványon, × n, és az első tag az "1/e" számhoz tart, amikor n a végtelenhez tart, és a második tényező, az "n" tetszőlegesen nagy, amikor n a végtelenhez tart, tehát A minden korlátnál nagyobb lehet. Magyarán mondva a jobboildali tagból alkotott általános tagú sorozat korlátlan.
|
|
| [160] S.Ákos | 2007-02-28 18:57:12 |
 Sziasztok!
Vki meg tudná mondani, hogy hogy lehetne meghatározni azt a legnagyobb egészet, melyre
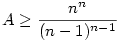
teljesül?(A egy tetszőleges poz. valós szám)
|
|
|
|
| [157] ScarMan | 2007-02-27 14:23:25 |
 Ha definiálunk egy új változót vagy függvényt vagy akármit, akkor az egyenlőségjel melyik oldalára kell írni a kettőspontot? Az új változó felől vagy a másik oldalra?
|
|
| [156] fermel | 2007-02-25 19:03:27 |
 Most már teljesen világos. Bár én a cserék alkalmazását kihagyom, de az indoklásom ugyanazokon az alapokon nyugszik. Nagyon sokat segítettél, köszönöm szépen. fermel
|
| Előzmény: [155] Sirpi, 2007-02-25 16:34:00 |
|
| [155] Sirpi | 2007-02-25 16:34:00 |
 Szóval felteszem, hogy le lehet tenni 5 pontot úgy, hogy ne keletkezzen rossz hármas. Ekkor nem lehet semelyik sorban 3 pont, mert akkor azok súlypontja a középső, így csak 2-2-1 lehet a megoszlás (nem feltétlen ebben a sorrendben), és ugyanez az oszlopokra is.
Azt állítom, hogy ha nincs rossz 3-as, akkor 2 sort megcserélve sem fog rossz 3-as keletkezni. Rossz 3-as csak úgy jöhet létre, hogy minden sorból és minden oszlopból egy elemet választok ki, hiszen egyik sor és oszlop sincs tele, az meg nem lehet, hogy 2-t az egyik sorból és 1-et egy másikból. Ilyenkor viszont a csere változatlanul hagyja az x- és y- koordináták összegét is, vagyis ha nem volt rossz hármas, akkor nem is jött létre új a csere hatására. Vagyis innentől szabadon csereberélhetem a sorokat és oszlopokat.
1. csere: a legfelső sorba viszek egy "dupla" (azaz 2 kiválasztott elemet tartalmazó) sort
2. csere: ebben a sorban a 2 elemet az első két helyre teszem
3. csere: felviszem a 2. sorba a másik dupla sort
4. csere: mivel az első 2 sorban 4 elem van, de csak 3 hely, ezért valahol egyeznek. Ezt az egyezést oszlopcserével az első oszlopba viszem
És ahogy már mondtam, most a (0,0) (1,0) (0,1) elemek ki vannak választva, és két eset van aszerint, hogy a 2. sorban melyik a másik kiválasztott elem. Innen úgy fejeződik be a bizonyítás, ahogy már leírtam.
|
| Előzmény: [154] fermel, 2007-02-25 16:14:08 |
|
| [154] fermel | 2007-02-25 16:14:08 |
 Pontosan eddig a segédállításig jutottam el én is és ennek a bizonyításánál akadtam el. A te bizonyításodból még sajnos az nem világos számomra, hogy miért csak az 1. és 2. eset jöhet szóba az első 4 pont vonatkozásában.( nem igazán értem a cseréket) Kifejtenéd kicsit bővebben? A bizonyítás többi része teljesen világos. Köszönöm. fermel
|
| Előzmény: [153] Sirpi, 2007-02-25 15:25:40 |
|
| [153] Sirpi | 2007-02-25 15:25:40 |
 8 nyilván nem elég (elég a koordináták 3-as maradékait kiírni):
(0; 0) (0; 0) (0; 1) (0; 1) (1; 0) (1; 0) (1; 1) (1; 1)
Itt csak úgy lehetne a súlypont rácspont, ha a négyzet valamelyik csúcsába esne, de akkor azt a csúcsot háromszor kellene kiválasztanunk, de mindegyik csak kétszer szerepel.
* * *
Ezek után be kellene látni, hogy 9 pontból viszont mindig kiválasztható a megfelelő 3.
Ennek belátásához egy segédállítás: a {0,1,2}×{0,1,2} halmaz 5 különböző elemét kiválasztva biztosan lesz köztük három, aminek súlypontja rácspont.
Ez azért van így, mert ha valamelyik sorban ki van választva 3 elem is, akkor készen vagyunk, ellenkező esetben viszont 2-2-1 a sorokban a kiválasztott elemek megoszlása, és ugyanez igaz az oszlopokra is. Veszem az első "dupla" sort és megcserélem az elsővel, majd oszlopcserékkel elérem, hogy a két elem az első 2 legyen a sorban. Ezután felviszem a 2. sorba a másik "dupla" sort, ennek valamelyik eleme felett is van elem, ezt az oszlopot megcserélem az első oszloppal. Innen két eset lehet az első két sor tekintetében:
1) a 4 pont egy négyzetet alkot a (0,0) (1,0) (0,1) (1,1) pontok által
2) a (0,0) (1,0) (0,1) (2,1) pontok vannak az első két sorban
Mindkét esetben nyilvánvaló, hogy a 3. sorban bármelyik elemet is választjuk ehhez a 4-hez, az létre fog hozni egy "rossz" ponthármast. Ezzel a segédállítást beláttuk.
Innen pedig készen vagyunk, mert maximum 4 különböző pontot választhatunk ki, mindegyiket legfeljebb kétszer (ha 3-szor választanánk, akkor az adott megháromszorozott pont önmagában meg fog felelni), ami összesen 8 pont legfeljebb.
Így beláttuk, hogy 9 pont kell legalább, hogy garantáltan kiválasztható legyen közülük 3 úgy, hogy azok súlypontja is rácspont.
|
| Előzmény: [152] fermel, 2007-02-25 12:46:22 |
|
| [152] fermel | 2007-02-25 12:46:22 |
 Valóban igaz,hogy nem is biztos, hogy létrejön háromszög. A feladatot akkor átfogalmazva: Hány rácspont elegendő, hogy biztosan találjak három olyat,hogy a megfelelő koordináták összege biztosan osztható legyen hárommal? Igazából egy kombinatorikai feladatot helyeztek geometriai csomagolásba, a lényeg számomra a kombinatorikai rész megoldása lenne. Most éppen ott tartok, hogy a válasz valószínűleg 9, de a bizonyítással gondjaim vannak. fermel
|
| Előzmény: [151] S.Ákos, 2007-02-23 19:22:32 |
|
|
|
|
|
| [147] tim20 | 2007-02-22 07:17:19 |
 Egy furcsa fa első nap 1,1/2-szeresére nőtt. Másnap az előző nap 1,1/3-szorosára, harmadnap az előző nap 1,1/4-szeresére és így tovább. Hány nap alatt nőtt meg az eredeti magasságának 100-szorosára?
|
|
| [146] fermel | 2007-02-17 15:06:02 |
 Mekkora az a legkisebb n, melyre biztosan igaz a következő? n db síkbeli rácspont esetén biztosan találunk köztük három olyat, amelyek által alkotott háromszög súlypontja is rácspont.
Köszönöm a segítséget. fermel
|
|
| [145] tim20 | 2007-02-16 13:01:02 |
 A könyvet sajnos nem tudom most beszerezni, de én azt mondom, hogy a második a nagyobb. Megerősítenél ha Te még a könyv oldalszámát is tudod? Előre is köszi.
|
| Előzmény: [144] jonas, 2007-02-16 12:09:19 |
|
|
| [143] tim20 | 2007-02-16 11:39:14 |
 Melyik a több? Fél tucat tucat tucat tucat, vagy hat tucat tucat tucat tucat? A második vagy az első vagy egyenlőek?
|
|
| [142] Lóczi Lajos | 2007-02-15 11:44:52 |
 Itthon a fuggvenyt inkabb Riemann-fuggvenynek hivjuk, a Dirichlet-fuggveny a racionalis szamok karakterisztikus fuggvenye (vagy annak "komplementere") szokott lenni.
|
| Előzmény: [141] jonas, 2007-02-14 23:12:49 |
|
|
| [140] nyida | 2007-02-14 22:13:33 |
 Helló! Kellene nekem kép, link, akármi arról a függvényről, amit Riemann talált ki, és az a szabály, hogy ha x irracionális, akkor a függvény 0, ha x racionális, akkor a függvény értékét a racionális szám közönséges törtalakjából a számláló 1-re cserélésével kapjuk. A függvényt 0 és 1 közt értelmezzük. Ez az első olyan függvény, ami minden racionális ponton szakad, minden irrac ponton folytonos. Kösz
|
|
| [139] Noémi | 2007-02-12 00:19:52 |
 Sziasztok! Éppen egy felejthetetlen kiselőadásra készülök, és véletlenül bukkantam erre az oldra. Így viszont kapva kapok eme páros , és soha vissza nem térő lehetőségen és a segítségeteket kérném. Én inkább (kb. 100%) humán beálítottságú vagyok, viszont, most a fősulin kéne tartanom egy előadást, melynek címe; elektromosság, mágnesesség. A tanárnő azt kérte, hogy mindenképpen CSAK érdekességeket említsek a témával kapcsolatban,(viszont az bármi lehet ami egy kicsit is kontektussal van e témával) és kerüljem az unalmas elméleti részt, melynek nagyon örültem, egészen addig amíg újfent rá nem jöttem, hogy értelmes ötleteknek még a halvány szikrája sem sziporkázik elmémben. Úgy gondoltam, miközben a fórum oldalain mozgattam szemgolyómat, hogy nektek biztos lennének jó ötleteitek eme fergeteges problémámra (remélem ennél nagyon soha nem lesz :) Én persze ha megadtok témát, annak utána nézek, s pótolom eme témával kapcsolatos hiányosságomat. Előre is köszönöm mindannyiotoknak; Noémi :)
|
|
| [137] thukaert | 2007-01-30 19:54:26 |
 A többváltozós diofantoszi egyenleteknél szükség van arra hogy megoldást rendezett n-es formájában adjuk meg, hiszen az hogy egy diofantoszi egyenletnek (2,1) megoldása az nem azt jelenti hogy az (1,2) is az.A sorrend itt a változók sorrendjét követi pl.: (x,y)=(2,1) ez pontosan azt jelenti hogy x=2 és y=1
vagy
(x,y,z)=(3,4,5) x=3 y=4 z=5
így (1,2) nem egyenlő (2,1)-el a rendezés tehát fontos,mert nem biztos hogy az egyenlet szimmetrikus a változóiban.
|
| Előzmény: [136] epsilon, 2007-01-30 13:08:45 |
|
| [136] epsilon | 2007-01-30 13:08:45 |
 Helló! Banális a kérdés, de, nem látom az értelmét, hogy egy adott diofantikus egyenlet egész megoldásainak keresésénél, miért teszik oda, hogy az (x,y) rendezett egész megoldásait kerseik? Mit kellene pluszban érteni a rendezés alatt, mint amit megszoktunk, hogy (x,y) nem ugyanaz mint (y,x), másvalamit? Vagy ezzel ki akarják zárni az (x,x) számpárokat?
|
|










