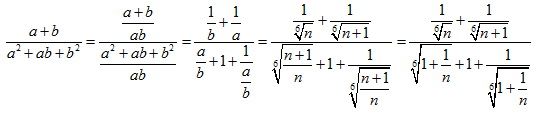| [1629] epsilon | 2012-01-18 09:39:59 |
 Tisztelt Fórumtagok! Továbbra is érdekel a kocka és a gömb metszésvonala, ígyhát bárkitől szívesen várok bármilyen ötletet. Üdv: epsilon
|
|
| [1628] Jhony | 2012-01-14 10:17:54 |
 köszönöm a választ,de a kédrésem arra utal ,vannak e hasonló iker prímek (magasabb számtartományokban is ) és,ha igen meddig - talán végtelen - szóval olyan iker prímek melyek összege plusz/minusz egy újabb ikerprímet generál (alkot)
|
| Előzmény: [1618] bily71, 2012-01-10 18:57:36 |
|
| [1627] epsilon | 2012-01-13 15:48:23 |
 Üdv lorantfy! Köszi, hogy a témában hozzászóltál, és előre köszönöm, ha rajzprogram is lesz a kezedügyében. Nekem nincs ilyen, gy közönséges rajzzal próbálkoztam kísérletezni, de én csak annyit látok, mintha 3 különálló körív lenne, ellenben ezek egymással kongruensek (szimmetria okok miatt). Jó lenne, ha megtudhatnám, hogy ez a sejtésem igaz-e? Előre is kösz mindennemű segítségedet! További szép napot!
|
| Előzmény: [1626] lorantfy, 2012-01-13 14:37:35 |
|
| [1626] lorantfy | 2012-01-13 14:37:35 |
 A gömb és a kocka lapjainak metszésvonalai körívek lesznek. Kétféle lap lesz ilyen szempontból. Az egyiken 3xgyök(3)/2 sugarú körív lesz, a másikon gyök(3)/3 sugarú körív. Ha rajzólóprogram közelben leszek, majd felteszek egy ábrát.
|
| Előzmény: [1625] epsilon, 2012-01-13 11:47:10 |
|
| [1625] epsilon | 2012-01-13 11:47:10 |
 Üdv mindenkinek, és először is BÚÉK! Máris lenne egy kérdésem: Adott egy 1 egységnyi kocka, annak valamelyik csúcsában mint középpontban r=2×gyök(3):3 sugarú gömböt rajzolunk. Érdekelne a kockafelület és a gömbfelület (közös) metszésvonala.Miből áll ez? Hogy látható? Valaki tudna-e segíteni ebben? Előre is köszönöm, további szép napot: epsilon
|
|
|
|
| [1622] Hölder | 2012-01-11 21:47:11 |
 Szerintem ugyanazt a mátrixot jelentik, mert a Jordan-blokkok megegyeznek. Persze lehet, hogy nem jól mondom. Kiss Emil algebra könyvében biztosan van erre is valami hasznos, de az okosabbak véleményét kérdem, mondjuk az ottani definíció alapján. Persze előfordulhat, hogy a definíció sem egyértelmű. Sajnos nem tudom a választ...
|
| Előzmény: [1620] jonas, 2012-01-11 10:16:03 |
|
|
|
| [1619] Hölder | 2012-01-11 10:08:28 |
 Legyen A és B két n-ed rendű valós elemekből álló mátrix. Igaz -e az, hogy akkor és csakis akkor hasonlóak egymáshoz, ha a Jordan-normálalakjuk megegyezik?
|
|
| [1618] bily71 | 2012-01-10 18:57:36 |
 Ellenpélda: 120-1=119=7.17, 120+1=11.11, 120=103+17.
A Goldbach-sejtés szerint minden 2-nél nagyobb páros előáll két prím összegeként. A 2n 1 alakú (páratlan) számok között a prímek egyre ritkulnak, ahogy n nő, így amit írtál, hogy legalább az egyik szomszéd prím, egyre ritkábban fordul elő, az ikerprím-sejtés ennek ellenére azt mondja, hogy végtelen sok esetben mindkét szám prím. 1 alakú (páratlan) számok között a prímek egyre ritkulnak, ahogy n nő, így amit írtál, hogy legalább az egyik szomszéd prím, egyre ritkábban fordul elő, az ikerprím-sejtés ennek ellenére azt mondja, hogy végtelen sok esetben mindkét szám prím.
|
| Előzmény: [1615] Jhony, 2012-01-10 18:23:35 |
|
|
| [1616] Jhony | 2012-01-10 18:48:07 |
 - egy matematikai ikerprímekkel kapcsolatos feladat,kérdésem, a következő ,,véges vagy végtelen azon ikerprímek sora ,(mint pl. az 5,7) melyek összege plusz,mínusz egy ,kettő újabb,másik prímszámot generál,alkot ?"
- sőt kicsit tovább megyek és azt kérdezem : ,,véges vagy végtelen azon ikerprímek sora melyek összege plusz,mínusz egy, másik,újabb ikerprímet generál,alkot ?" - erre példa az (5,7) lásd. 5+7=12 +/- 1 = 11/13
- a válaszokat és a segítséget előre is köszönöm !
Üdvözlettel,Jhony !
|
| Előzmény: [1615] Jhony, 2012-01-10 18:23:35 |
|
| [1615] Jhony | 2012-01-10 18:23:35 |
 Köszönöm szépen a választ ! --- nos a kettő közül,az egyikhez hasonló ez lenne ,,két prímszám összege plusz,minusz egy legalább egy ,de lehetséges,hogy kettő újabb prímszámot(számokat) generál(alkot)" .
|
| Előzmény: [1614] HoA, 2012-01-09 22:25:17 |
|
| [1614] HoA | 2012-01-09 22:25:17 |
 Attól tartok, bármilyen óvatosan fogalmazol is, nemhogy manapság, de szerintem az utóbbi kétszáz évben szinte reménytelen, hogy érdekes vagy hasznos - mások által nem ismert és nem triviális - sejtése legyen valakinek, aki nem rendelkezik az érintett matematikai ágazat mély ismeretével. Itt a fórum támái között több helyen találsz utalást hasonló kérdésekre. Például Goldbach sejtés, ikerprím sejtés.
|
| Előzmény: [1613] Jhony, 2012-01-09 17:30:46 |
|
| [1613] Jhony | 2012-01-09 17:30:46 |
 - megtudná-e mondani valaki mi a helyzet manapság ,ha valakinek van egy vagy kettő matematikai sejtése - már csak az a kérdés,hogy máig senki által nem említett sejtések-e és ...,hogy a matematika ,,világában" mennyire számítanak ,számítanának ,,érdekes",mondjuk ,,hasznos" sejtésnek - bizonyos szemszögből nézve ...
- a válaszokat,hozzászólásokat előre is köszönöm !
|
|
|
| [1611] bloghus | 2012-01-09 13:07:50 |
 Egy cég kétféle terméket gyárt. A P(x; y) -3x(négyzet)-y(köb)+6xy profitot (millió forint) fejezi ki a termékek árainak függvényében (ezer forint). A termékek milyen egységára mellett maximális a profit és mennyi az értéke?
|
|
|
|
| [1608] Jhony | 2012-01-05 14:53:52 |
 - meg tudná mondani valaki hol van a hiba az alábbi bizonyításban --- ,ha van ??? --- és,hogy azt bizonyítja e helyesen amit gondoltam ,vagyis azt a bizonyos ,,sejtést" ?
1. subst. - let p and k , two prime numbers greater or equal 2,from the set of prime numbers, P, in the form : p=2a + 1 and k=2b + 1 , such that a and b are natural numbers,from the set of natural numbers N, - let m=2n ,m greater or equal 4,even number,from the set of natural numbers N and n grater or equal 2,natural number from set of natural numbers N, 2. concl. - every even integer greater than 2 can be expressed as the sum of two primes 3. prove:- by ,,reductio ad absurdum” * - step 0. for n=2 --- m=4 --- 4=2+2 ** - step 1. for - if n is greater or equal 3 so always will be a number a and b such that n=a + b + 1 - prove. 3=1+1+1 4=2+1+1 5=2 +2+1 ................ n=a+b+ 1 - so for n=k than k=a+b+1 - suppose that is true - for k+1=(a+b+1)+1=(k)+1=k+1 - so for k+1 is true - for n grater than 2 always will be a number a and b such that n =a+b+ 1 *** - step 2. - every even integer greater than 4 can be expressed as the sum of two primes m=p+k - prove by ,,reductio ad absurdum" - so than m is not equal p+k - so than 2n is not equal 2a+1+2b+1 - so than 2n is not equal 2a+2b+2 / divide both sides by 2 - so than n is not equal a+b+1 - so what is in contradiction with the proof from step 1. where n=a+b+1 was proved that is true - so than m=p+k is proved that is true so,, every even integer greater than 4 can be expressed as the sum of two primes” --- q.e.d.
- köszönöm szépen és bocsánat a zavarásért !
|
|
|
|
| [1605] logarlécész | 2012-01-02 17:44:53 |
 Ezek után mit csinálunk? Rendezzük, vagy azt mondjuk, hogy ha n tart a végtelenbe, akkor kb. n=n+1 => a=b => a kifejezés: 2/3a a tart a végtelenbe => 2/3a->0
A második attól függetlenül, hogy kihozza a jó megoldást(?), inkább fizikus megoldásnak tűnik a kerekítgetéssel. :-)
Az igazi megoldási menetben beírjuk a kifejezéseket és rendezgetjük tovább?
|
| Előzmény: [1601] lorantfy, 2011-12-30 16:48:24 |
|









 1 alakú (páratlan) számok között a prímek egyre ritkulnak, ahogy n nő, így amit írtál, hogy legalább az egyik szomszéd prím, egyre ritkábban fordul elő, az ikerprím-sejtés ennek ellenére azt mondja, hogy végtelen sok esetben mindkét szám prím.
1 alakú (páratlan) számok között a prímek egyre ritkulnak, ahogy n nő, így amit írtál, hogy legalább az egyik szomszéd prím, egyre ritkábban fordul elő, az ikerprím-sejtés ennek ellenére azt mondja, hogy végtelen sok esetben mindkét szám prím.
 3 , akkor van olyan a és b egész, hogy n=a + b + 1 , csak ezeket nem szabad összekeverni az elején definiált, k-hoz ill. p-hez tartozó a-val és b-vel.
3 , akkor van olyan a és b egész, hogy n=a + b + 1 , csak ezeket nem szabad összekeverni az elején definiált, k-hoz ill. p-hez tartozó a-val és b-vel.
 .
.