|
|
|
| [1708] Kemény Legény | 2012-03-18 20:35:35 |
 733...32=5377...7288...89
még jobb választás, erre B 7.5 jön ki. Ez már közel lehet a megoldáshoz, ugyanis az OEIS adatbázisban A069665 néven további elemei is meg vannak adva a sorozatnak, amik kb. ilyen átlagot produkálnak (de nincs semmi dokumentum a további referenciák között). 7.5 jön ki. Ez már közel lehet a megoldáshoz, ugyanis az OEIS adatbázisban A069665 néven további elemei is meg vannak adva a sorozatnak, amik kb. ilyen átlagot produkálnak (de nincs semmi dokumentum a további referenciák között).
|
| Előzmény: [1707] Kemény Legény, 2012-03-18 20:27:15 |
|
| [1707] Kemény Legény | 2012-03-18 20:27:15 |
 Nem biztos, hogy közelebb visz a megoldáshoz - már ha egyáltalán megválasztható a kérdés - de négyzetszámok esetén B 6, ugyanis 6, ugyanis
533...32=2844...4088...89,
ahol n db 3-as követi az 5-öst, illetve n-1 db 4-es és 8-as van egymás mellett az eredményben. Talán szerencsésebb próbálkozással ennél jobb is található, idő hiányában nem vizsgáltam tovább, amint 4.5-nél jobbat találtam, megálltam.
|
| Előzmény: [1706] Sirpi, 2012-03-17 23:21:36 |
|
| [1706] Sirpi | 2012-03-17 23:21:36 |
 Találtam egy új problémát, nem tudom, mennyire van kivesézve.
Legyen a1,a2,... egy végtelenbe tartó egész számsorozat, és számjegyátlagának liminf-je legyen A, limsup-ja B.
Ekkor nyilván 0 A A B B 9, de nevezetes sorozatoknál tudunk ennél többet is mondani? 9, de nevezetes sorozatoknál tudunk ennél többet is mondani?
Például ha an=n2, akkor A = 0, és B 4,5, de B-re van jobb? Az 1, 2, stb. jegyű számokra a maximális számjegyátlag így alakul (optimum, számjegyátlaga): 4,5, de B-re van jobb? Az 1, 2, stb. jegyű számokra a maximális számjegyátlag így alakul (optimum, számjegyátlaga):
9 9.000000
49 6.500000
289 6.333333
6889 7.750000
97969 8.000000
698896 7.666667
9696996 7.714286
79869969 7.875000
876988996 7.777778
És ha an=2n, arra tud valaki bármi építő jellegűt?
|
|
|
| [1704] SmallPotato | 2012-03-16 21:21:14 |
 Gyanús volt a képlet, utánakerestem (ha már a közzétevő titkot csinál belőle).
A Colebrook–White-képletről van szó; a D az egyenértékű csőátmérő (teljes keresztmetszetben kitöltött cső esetében a valódi belső átmérő); Re a Reynolds-szám, amely a viszkozitás, a csőátmérő és az áramlási sebesség függvényében több nagyságrendet fog át.
A legszebb, hogy a szócikkben szerepel is, hogy az egyenlőséget a  csősúrlódási tényező iteratív kiszámítására használják. csősúrlódási tényező iteratív kiszámítására használják.
|
| Előzmény: [1703] jonas, 2012-03-16 20:50:24 |
|
|
| [1702] jonas | 2012-03-16 20:47:33 |
 Azért még egy kérdésem van. A [1691] vagy a [1690] egyenletet kell nézni? Esetleg külön-külön mindkettő érdekel? Kemény Legény az előbb észrevette, hogy ezek különböznek.
|
| Előzmény: [1700] TLevi, 2012-03-16 11:07:46 |
|
| [1701] Lóczi Lajos | 2012-03-16 13:23:44 |
 A válasz már kétszer elhangzott korábban a kérdésedre: nincs "egyszerű megoldás erre az egyenletre", csak olyan, amelyik speciális függvényt tartalmaz. (És ez nem azon múlik, hogy valakinek milyen "mennyiségű és milyenségű" matematikai ismerete van -- az egyenlet fajtája ilyen.)
Az a program (pl. Excel), amelyet a konkrét számolásra szeretnél használni, tud a (korábban már említett) Lambert-féle W-függvénnyel dolgozni? Ha igen, felírok egy formulát, amelyet a D és Re paraméterekkel tudsz manipulálni és az egyenlet megoldását adja  -ra. -ra.
|
| Előzmény: [1700] TLevi, 2012-03-16 11:07:46 |
|
| [1700] TLevi | 2012-03-16 11:07:46 |
 Igen, az lg tízes alapú logaritmust jelent. Igen, a 2,51 és 3,71 konstansokat csak három jegy pontosan ismerem. Tovabb folytatnam ... a lambdat meg mindig nem sikerul kifejeznem (kello mennyisegi es milyensegu matematikai ismereteim hianya miatt). Tehat, ha kapnek egy egyszeru megoldast erre az egyenletre (pl. igy: lambda egyenlo..... - tehat nem "1/gyok lambda egyenlo.....), az megint nagyon jo lenne ha ezt parametrikusan tudnam valtoztatni a tobbi valtozo (D es Re) fuggvenyeben (pl. Excelbe beirt keplettel). Megegyszer: sajnos a matek nem az erossegem!
Tisztelettel TLevi
|
| Előzmény: [1698] jonas, 2012-03-15 09:17:19 |
|
| [1699] TLevi | 2012-03-16 10:58:19 |
 szia!
Hogy miert van ket mertekegyseg az egyenletben? ezek az ertekek igy vannak megadva mertekegysegekkel, de ahogy ertem, a lambdanak nincs mertekegysege.
|
| Előzmény: [1697] jonas, 2012-03-15 09:12:48 |
|
|
|
| [1696] Kemény Legény | 2012-03-15 08:52:18 |
 Nem használhatsz valamilyen matematikai segédprogramot, ami numerikusan megoldja az egyenletet? Például Maple, Mathematica, Matlab,... mind rendelkezik beépített numerikus egyenletmegoldóval.
Azt mellesleg tudod, hogy az 1690-es és 1691-es képleteid nem ekvivalensek? (egy negatív előjel nem stimmel).
Az 1691-es megoldása numerikusan:   1.3123. Ezt online is megkaphatod a WolframAlpha segítségével. 1.3123. Ezt online is megkaphatod a WolframAlpha segítségével.
|
| Előzmény: [1695] TLevi, 2012-03-15 08:06:04 |
|
| [1695] TLevi | 2012-03-15 08:06:04 |
 Kosz a segitseget!
De... sajnos a matek nem az eros oldalam Lehetseges, hogy ha adok ertekeket, akkor kaphatnek egy erteket a labdara?
ha igen, akkor:
D=0,051545455 [m] k=0,07 [cm] Re=5885548.364 (valtoztatdato kellene legyen de ebben az esetben ennyi)
Tehat, ha ezekkel sikerulne egy lambda erteket kapni, az jo lenne (erre az esetre...de az meg jobb lenne, ha a lamdat a D es a Re fuggvenyeben lehetne valtoztatni)
Elore is kosz' a segitseget!
Tisztelettel TLevi
|
| Előzmény: [1694] Lóczi Lajos, 2012-03-14 18:43:43 |
|
| [1694] Lóczi Lajos | 2012-03-14 18:43:43 |
 Általában az ilyen transzcendens egyenletekből véges sok elemi függvénnyel nem lehet kifejezni a változókat. A te példád is ilyen. Tulajdonképpen csak a numerikus megoldás jön szóba.
Ha mégis kell valamilyen "formula", akkor  kifejezhető pl. a Lambert-féle W-függvénnyel, lásd az Examples részt. Praktikusan persze ez nem jelent sok segítséget. kifejezhető pl. a Lambert-féle W-függvénnyel, lásd az Examples részt. Praktikusan persze ez nem jelent sok segítséget.
|
| Előzmény: [1693] TLevi, 2012-03-14 14:53:29 |
|
| [1693] TLevi | 2012-03-14 14:53:29 |
 ...A Re - t keplettel kellett kiszamitani...hat Reynolds szam, de valtoztathato mas parameterek fuggvenyeben. A "lambda" is valtoztathato egyutthato. (linearis terheles-vesztessegi egutthato)...(remelem jo a forditas)
|
| Előzmény: [1692] Lóczi Lajos, 2012-03-14 14:43:54 |
|
|
| [1691] TLevi | 2012-03-14 13:30:41 |
 Sziasztok!...variacio egy temara:
Segitseget szeretnek egy egyenlet megoldasahoz! Az egyenletet mellekelem "*.jpg" formatumban. Nem tudom, hogyan kell kifejeznem a "lambdat" a tobbi ertek fuggvenyeben. (csak a lambda ismeretlen) Elore is koszonom a segitseget!
|
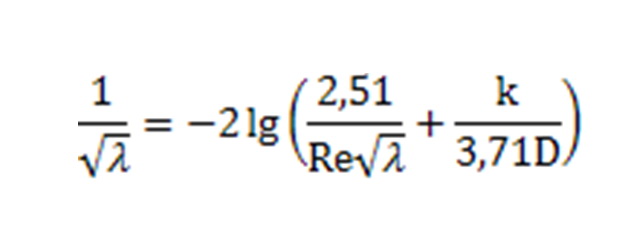 |
|
| [1690] TLevi | 2012-03-14 13:28:54 |
 Sziasztok!
Segitseget szeretnek egy egyenlet megoldasahoz! Az egyenletet mellekelem "*.jpg" formatumban. Nem tudom, hogyan kell kifejeznem a "lambdat" a tobbi ertek fuggvenyeben. (csak a lambda ismeretlen) Elore is koszonom a segitseget!
Udv, TLevi
|
 |
|
| [1689] Lóczi Lajos | 2012-03-14 09:31:59 |
 Először is pontosítanod kell a feladatot.
Pl. x a változó? Valós?
 egy paraméter? Valós? Pozitív? 1-nél nagyobb? egy paraméter? Valós? Pozitív? 1-nél nagyobb?
Az aszimptotikus egyenlőséget hol érted? Ha x  ? (Különben a függvény nem is invertálható mindenhol.) ? (Különben a függvény nem is invertálható mindenhol.)
Milyen tételre hivatkoznak?
Próbáld az aszimptotikus egyenlőség két oldalán szereplő kifejezések hányadosának limeszét vizsgálni úgy, hogy "új változót" vezetsz be és így az inverzfüggvény kiküszöbölhető.
|
| Előzmény: [1688] Zine, 2012-03-13 21:38:16 |
|
| [1688] Zine | 2012-03-13 21:38:16 |
 Nem szeretnék megoldást kapni, csak ötletet szeretnék kérni, hogyan lehetne belátni a következőt:
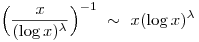
ahol a baloldal a -1-edik hatvány az inverzfüggvényt jelöli. Egy tétel felhasználásával ki tudom hozni, azonban magát a tételt nem teljesen értem, így ettől különböző megoldást szeretnék találni. Előre is köszönöm!
|
|
|





 7.5 jön ki. Ez már közel lehet a megoldáshoz, ugyanis az OEIS adatbázisban A069665 néven további elemei is meg vannak adva a sorozatnak, amik kb. ilyen átlagot produkálnak (de nincs semmi dokumentum a további referenciák között).
7.5 jön ki. Ez már közel lehet a megoldáshoz, ugyanis az OEIS adatbázisban A069665 néven további elemei is meg vannak adva a sorozatnak, amik kb. ilyen átlagot produkálnak (de nincs semmi dokumentum a további referenciák között). A
A
 csősúrlódási tényező iteratív kiszámítására használják.
csősúrlódási tényező iteratív kiszámítására használják.

 1.3123. Ezt
1.3123. Ezt 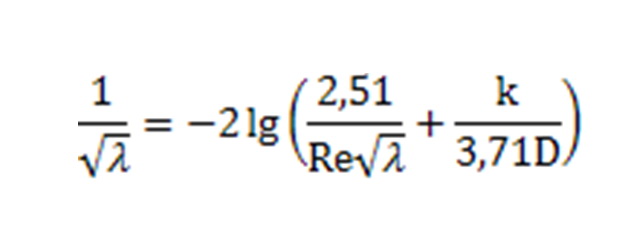


 ? (Különben a függvény nem is invertálható mindenhol.)
? (Különben a függvény nem is invertálható mindenhol.) 