| [1736] sakkmath | 2012-04-08 16:25:51 |
 Megnéztem a könyvben a faladatot. A szerző a 86 - 88. oldalakon öt megjegyzést fűz a megoldáshoz. Az 1. megjegyzése még jó, a többi hibás! Például a 2. megjegyzés hibája ez: "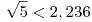 ". ".
Scharnitzky a 3. megjegyzésben elkövetett súlyos hibát a 4. és 5. sorszámúakban még tovább is ragozta.
|
| Előzmény: [1731] kovátsnorbi1994, 2012-04-07 21:30:34 |
|
|
| [1734] Róbert Gida | 2012-04-08 11:51:50 |
 De ez például már igaz: 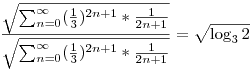
"Nem értem, hogy az egyenlőség két oldalán lévő érték hogyan lesz egyenlő, vagyis miért emelhető-e szumma jel elé az összegzési indexet is tartalmazó hányados, ha véges sok esetben nincs egyenlőség a jobb- és baloldal között."
Egy mondatban ennyi zöldséget rég olvastam.
|
| Előzmény: [1731] kovátsnorbi1994, 2012-04-07 21:30:34 |
|
|
|
| [1731] kovátsnorbi1994 | 2012-04-07 21:30:34 |
 Jó estét minden Fórumozónak!
A segítségetekre lenne szükségem egy példatárban olvasott megjegyzés értelmezésével kapcsolatban: A megjegyzéshez kapcsolódó feladat az /1989-1992/-es Egyetemi Felvételi Feladatok (Scharnitzky-féle) példatár 87. oldalán olvasható, ahol konvergens Taylor-sorral adnak felső becslést  értékére. Itt leírják a következő átalakítást, ami nem világos számomra : értékére. Itt leírják a következő átalakítást, ami nem világos számomra :
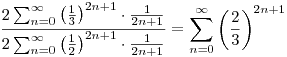
Megnéztem konkrét, véges sok esetre az átalakítást: A baloldali összeg kifejtésére (véges sok esetben) a következőt kaptam:
![\frac{2\cdot\sum_{n=0}^3\left(\frac13\right)
^{2n+1}\cdot{\frac1{2n+1}}}{2\cdot\sum_{n=0}^3\left(\frac12\right)
^{2n+1}\cdot{\frac1{2n+1}}}=\frac{2\cdot[\left(\frac13\right)+\left(\frac13\right)^3\cdot
\left(\frac13\right)+\left(\frac13\right)^5\cdot
\left(\frac15\right)+\left(\frac13\right)^7\cdot
\left(\frac17\right)]}{2\cdot[\left(\frac12\right)+\left(\frac12\right)^3\cdot
\left(\frac13\right)+\left(\frac12\right)^5\cdot
\left(\frac15\right)+\left(\frac12\right)^7\cdot
\left(\frac17\right)]}](keplet.cgi?k=A647FD6ED59CAC20)
Míg a jobboldali szumma kifejtésére:
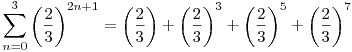
Nem értem, hogy az egyenlőség két oldalán lévő érték hogyan lesz egyenlő, vagyis miért emelhető-e szumma jel elé az összegzési indexet is tartalmazó 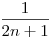 hányados, ha véges sok esetben nincs egyenlőség a jobb- és baloldal között. hányados, ha véges sok esetben nincs egyenlőség a jobb- és baloldal között.
A választ köszönöm, és békés ünnepeket kívánok mindenkinek!
|
|
|
| [1729] jenei.attila | 2012-03-25 17:06:28 |
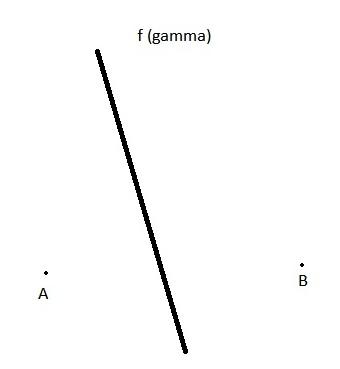
 Mivel az f szögfelező, ezért az A pont f-re vett A' tükörképe rajta van a CB egyenesen. Tehát tükrözd A-t f-re (A'-őt kapod), majd az A'B és f egyenes metszéspontja megadja a C csúcsot.
|
| Előzmény: [1728] kler69, 2012-03-25 16:52:41 |
|
| [1728] kler69 | 2012-03-25 16:52:41 |
 Kedves Mindenki! Sajnos már régen voltam iskolás, és a fiam ált. iskolás matekházija kifogott rajtunk. Kérem, aki tud, segítsen! A feladat: Adott egy háromszög A és B csúcsa, valamint a harmadik csúcsban levő szög szögfelezője. Szerkesszük meg a háromszöget! Köszönöm szépen!
|
 |
|
|
|
| [1725] Fálesz Mihály | 2012-03-23 16:32:36 |
 Én inkább a 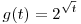 függvényt vizsgálnám. A második derivált mutatja, hogy g a függvényt vizsgálnám. A második derivált mutatja, hogy g a ![[0,1]\subset\Big[0,\frac1{(\ln2)^2}\Big]](keplet.cgi?k=6C89DEA734520B16) intervallumban konkáv: intervallumban konkáv:
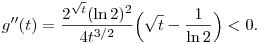
Ezért hát a Jensen-egyenlőtlenséget a g függvényre és az sin2x, cos2x pontokra felírva,
2sin x+2cos x 2|sin x|+2|cos x|=g(sin2x)+g(cos2x) 2|sin x|+2|cos x|=g(sin2x)+g(cos2x)
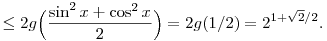
|
| Előzmény: [1722] spongya, 2012-03-22 23:24:12 |
|
|
|
| [1722] spongya | 2012-03-22 23:24:12 |
 "Ha sikerülne elemi eszközökkel belátni, hogy 2sin(x) alulról konkáv, ..."
Nekem + az jött ki, hogy ![[0;\frac13]](keplet.cgi?k=81A3E1FD6E32E2F2) -ban 2sin(x) alulról konvex. Sőt, a konvexitási tartomány jobbra még kicsit szélesíthető is. Vagy rosszul látom? -ban 2sin(x) alulról konvex. Sőt, a konvexitási tartomány jobbra még kicsit szélesíthető is. Vagy rosszul látom?
|
| Előzmény: [1720] HoA, 2012-03-22 20:05:27 |
|
| [1721] Lóczi Lajos | 2012-03-22 22:56:02 |
 Valamilyen a>1 esetén tekintsük az asin (x)+acos (x) függvényt a [0,2 ) intervallumon. Ha pl. a=2, akkor f-nek pontosan 2 szélsőértékhelye van. ) intervallumon. Ha pl. a=2, akkor f-nek pontosan 2 szélsőértékhelye van.
Van olyan a>2 érték, amikor ez nem igaz? Mi az "első" ilyen kritikus érték?
|
|
|
| [1719] Hölder | 2012-03-22 12:21:33 |
 Én egy kicsit máshogy közelítettem meg a dolgot, bár el kell ismerjem, először én is úgy próbáltam, mint te. Szóval 2 a sinx-ediken /(sinx) = 2 a cos x-ediken /cosx (nyilván sinx= 0 és cosx=0 nem jöhet szóba, ezért nyugodtan oszthatunk vele).És itt érdemes bevezetni a g(x) =2 az x-ediken /x függvényt, ezt vizsgálni a [-1,1]-ban, hiszen az argumentumok sinx és cos x. Ha megnézed, ennek 1/ln 2-ben lesz szélsőértéke, ami 1-nél nagyobb, tehát előtte monoton a függvény, amiből adódik, hogy sinx=cosx, azaz tgx=1, innen jönnek a szélsőértékek, de ez sajnos nem elemi megoldás, és valahogy úgy érzem valami nagyon trükkös elemi megoldás is van, csak én nem találtam meg. Amúgy hogy lehet itt matematikai dolgokat beírni?
|
| Előzmény: [1718] Lóczi Lajos, 2012-03-21 21:33:58 |
|
| [1718] Lóczi Lajos | 2012-03-21 21:33:58 |
 Érdekes, hogy deriválással könnyen meghatározható az 5 /4-nél lévő minimum (csak egy Bolzano-tétel -- ez az a szélsőérték, ami neked is kijött már elemi módszerekkel), de a /4-nél lévő minimum (csak egy Bolzano-tétel -- ez az a szélsőérték, ami neked is kijött már elemi módszerekkel), de a  /4-nél lévő maximummal meg kellett egy kicsit küzdenem. /4-nél lévő maximummal meg kellett egy kicsit küzdenem.
Vagyis a kérdésem az, hogy hogyan lehetne minél egyszerűbben belátni, hogy a
tg(x)=2sin (x)-cos (x)
egyenletnek a [0,2 ] intervallumban pontosan 2 gyöke van? (Az x ] intervallumban pontosan 2 gyöke van? (Az x ( ( /2,2 /2,2 ] intervallum tehát könnyű, ami szerintem nem látszik egyszerűen, az az x ] intervallum tehát könnyű, ami szerintem nem látszik egyszerűen, az az x [0, [0, /2) tartomány.) /2) tartomány.)
|
| Előzmény: [1717] Hölder, 2012-03-20 20:46:47 |
|
|
|
| [1715] Hölder | 2012-03-20 10:31:26 |
 Sziasztok!
Van egy feladat, amire próbáltam elemi (differenciálás nélküli) megoldást is keresni, de nem találtam. Ha nektek van megoldásotok, amiben pl. közepek, Jensen-egyenlőtlenség szerepel, stb., tehát elemibb eszközök, akkor azt ossza meg velem is.
A feladat: keressük meg a 2 a sin x-ediken +2 a cos x-ediken függvény maximumát!
megjegyzés: a minimumra van elemi megoldás (közepek), a maximumot pedig "nyilván" 45 foknál veszi fel.Elnézést, hogy nem szépen írtam be a feladatot.
|
|
|
|
|









 2|sin x|+2|cos x|=g(sin2x)+g(cos2x)
2|sin x|+2|cos x|=g(sin2x)+g(cos2x)
 ) intervallumon. Ha pl. a=2, akkor f-nek pontosan 2 szélsőértékhelye van.
) intervallumon. Ha pl. a=2, akkor f-nek pontosan 2 szélsőértékhelye van. 
 (
(
