| [1788] Róbert Gida | 2012-11-25 12:57:23 |
 Egyrészt ordít róla a binomiális tétel, ki is lehet hozni egy explicit formulát mindkét oldalra. Komplex számokkal könnyebb az út, de ez valósban is megy. A Mathematica viszont egy érdekes alakot is ad a két oldal különbségére:
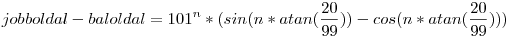
|
| Előzmény: [1786] polarka, 2012-11-25 01:01:03 |
|
| [1787] Lóczi Lajos | 2012-11-25 12:51:31 |
 Nem mondtad meg, hogy n milyen számhalmaz eleme. Vegyük most természetes számnak az egyszerűség kedvéért.
Legyen például z a 99+20i komplex szám. Ekkor, valós és képzetes részeket használva, az egyenlőtlenség átírható a 10.re(zn)<im(zn) alakba. Polárkoordinátákkal folytatva, a
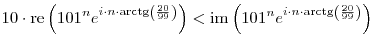
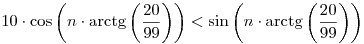
és
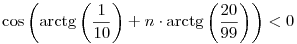
ekvivalens alakokat kapjuk. Mivel a koszinusz (n-ben) szigorúan monoton növő argumentuma n=0 esetén a (0, /2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a ( /2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a ( /2,3 /2,3 /2) intervallumba. Ez pedig n=8 esetén történik meg leghamarabb. /2) intervallumba. Ez pedig n=8 esetén történik meg leghamarabb.
|
| Előzmény: [1786] polarka, 2012-11-25 01:01:03 |
|
| [1786] polarka | 2012-11-25 01:01:03 |
 Mely legkisebb n-re teljesül az egyenlőtlenség?
Több n-re behelyettesítve kaptam, hogy n>=8.
Viszont arra lennék kíváncsi, hogy próbálgatás nélkül hogyan lehetne a választ megkapni.
|
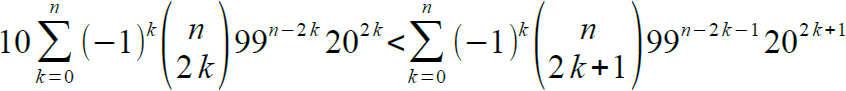 |
|
| [1785] Róbert Gida | 2012-11-11 17:55:57 |
 Én speciel már semmin nem csodálkoznék.
http://www.vg.hu/gazdasag/gazdasagpolitika/demjan-akar-assunk-godrot-hazaarulas-nem-lehivni-az-eu-penzeket-390676
"Demján meglátása szerint nem szabadna olyan tudósokat képezni, akik például a bogarak életét kutatják." Tippem szerint jövőre már nem indítanak biológia tagozatos osztályokat. Specmatosok is bármikor sorra kerülhetnek.
|
| Előzmény: [1783] sulc, 2012-11-07 21:03:08 |
|
| [1784] HoA | 2012-11-08 17:46:06 |
 Vagyis - nem akarva csökkenteni egyikük matematikusi érdemeit sem - hasonlóan járt, mint Skljarszkij a Szovjetúnióban, mikor a háburú utáni évek kelet-európai hangulatában összekeverték a háború áldozatainak járó részvétet és tiszteletet a szakmai érdemekkel. Lásd Billiárdgolyók téma [63] .
|
| Előzmény: [1773] logarlécész, 2012-10-27 23:43:55 |
|
| [1783] sulc | 2012-11-07 21:03:08 |
 A hír téves. Ilyen tudtommal nem hangzott el a hétfői szülői értekezleteken. Szépen kérek mindenkit, hogy ne terjesszen ellenőrizetlen információkat! A következő tanévre is meg lesz hirdetve a 6 osztályos spec. mat. tagozatos osztály a szegedi Radnótiban. Schultz János, Radnóti Miklós Gimnázium, Szeged.
|
|
| [1782] koma | 2012-11-07 20:13:18 |
 Sziasztok!
Köszönöm szépen a válaszokat!(elnézést a kései üzenetért, de sajnos nagyon ritkán jutok internet kapcsolathoz)
Több fórumon azt olvastam, hogy a következő tanévtől állambácsi megszünteti a spec matekos tagozatokat(állítólag ez elhangzott a szegedi radnóti szülői értekezletén, más a fazekassal kapcsolatosan erősítette meg ezt a pletykát)
Ti tudtok erről valamit?
Nagyon félek tőle, hogy igaz a hír...
|
|
|
|
| [1779] koma | 2012-10-29 20:33:02 |
 és azt leírnád esetleg,hogyan jött ki?
|
|
|
|
|
| [1775] koma | 2012-10-29 16:59:52 |
 Melyik az a legkisebb természetes szám amelynek 25 osztója van? Ha valaki tudna ebben segíteni megköszönném!
|
|
| [1774] logarlécész | 2012-10-27 23:59:09 |
 Az alapján van esély megérteni a működési elvet? (Mondjuk, ha valaki jobban tud programozni, mint egy angol szöveget megérteni.)
Kár, hogy magyarul nincs erről semmi. De ha valaki véletlenül mégis csak tud valamit ajánlani... :-)
Ja, és azért köszönöm a segítséget!
|
| Előzmény: [1772] jonas, 2012-10-27 22:38:17 |
|
|
|
|
| [1770] jonas | 2012-10-27 22:24:47 |
 Van egy elég régi angol nyelvű cikk, ami hatékony (lényegében lineáris idejű) algoritmust ad erre. Úgy emlékszem, láttam már szkennelt változatát. Megpróbálom megkeresni.
|
| Előzmény: [1768] logarlécész, 2012-10-27 18:45:22 |
|
| [1769] Hölder | 2012-10-27 21:34:08 |
 Sziasztok! Valaki meg tudná mondani, hogy ki volt Schweitzer Miklós? Mostanában ez eléggé aktuális kérdés is lehet,hiszen éppen most van a róla elnevezett verseny,de nem találtam róla semmit a google által. Válaszotokat előre is köszönöm.
|
|
| [1768] logarlécész | 2012-10-27 18:45:22 |
 Sziasztok!
Olyan algoritmust keresek, amely eldönti egy gráfról, hogy síkba rajzolható-e.
Sajnos csak angol nyelven találtam róla anyagot, amit sajnos nem nagyon értek.
Ha valaki tudna segíteni (akár magyar anyag mutatásával, akár az angol anyag lefordításával, akár egyéni ismereteinek továbbadásával) nagyon örülnék neki.
|
|
|
|
|
| [1764] Zine | 2012-06-03 17:28:36 |
 Ha jól emlékszem valahol itt a fórumon olvastam erről, csak most nem találtam meg és kíváncsi lennék: a természetes számokat a műveleteikkel együtt a Peano-aritmetika axiomatikusan megadja; a többi számhalmazt milyen algebrai bővítésekkel kapjuk meg a természetes számokból? Előre is köszönöm!
|
|




 /2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a (
/2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a (
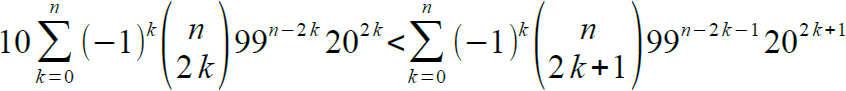


 1+1).(
1+1).(

