Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[1837] koma	2013-02-25 21:00:06
köszönöm szépen
Előzmény: [1836] Zine, 2013-02-25 17:22:56

[1836] Zine	2013-02-25 17:22:56
Multivariate function, multivariable function, vector-valued function, etc. Németben nem tudok autentikus segítséget nyújtani.
Előzmény: [1835] koma, 2013-02-25 07:48:52

[1835] koma

2013-02-25 07:48:52

Sziasztok!

Valaki meg tudná esetleg mondani, hogy a "többváltozós függvények" kifejezést hogyan mondják angolul illetve németül?

Köszönöm a segítséget!:)

[1834] Ménkűnagy Bundáskutya	2013-02-22 17:13:04
Még olyan se.
Előzmény: [1832] Kőrösi Ákos, 2013-02-22 16:50:47

[1833] Ménkűnagy Bundáskutya	2013-02-22 17:12:47
Nincs.
Előzmény: [1831] Kőrösi Ákos, 2013-02-22 16:47:07

[1832] Kőrösi Ákos	2013-02-22 16:50:47
Vagy hogy konvergens-e egyeltalán.
Előzmény: [1831] Kőrösi Ákos, 2013-02-22 16:47:07

[1831] Kőrösi Ákos	2013-02-22 16:47:07
Legyen adott egy természetes számokból képzett végtelen sorozat. Van-e olyan algoritmus, mely eldönti a sorozat reciprokösszegét?

[1830] w	2013-02-14 07:27:32
Fogod magad, kipróbálod gyöknek (behelyettesíted) az 1-et. Aztán a (-1)-et. Rájössz, hogy ezek irracionális helyettesítési értékeket adnak a $\sqrt6$ miatt, így a $\sqrt6$ -ot helyettesíted be, és kapod, hogy az megoldás. És innen $x^3-7x+\sqrt6=(x-\sqrt6)(x^2+\sqrt6x-1)$ , amit befejezni már ujjgyakorlat. Mindig érdemes először kitartóan gyököket keresni az egyenletnek.
Előzmény: [1829] Lapis Máté Sámuel, 2013-02-14 02:00:25

[1829] Lapis Máté Sámuel	2013-02-14 02:00:25
Köszönöm, de programok nélkül hogyan kéne megcsinálni?
Előzmény: [1825] Lapis Máté Sámuel, 2013-02-13 18:50:40

[1828] jonas	2013-02-13 22:38:02
Szóval észre kell venni, hogy az $x = \sqrt6$ véletlenül pont megoldás?
Előzmény: [1825] Lapis Máté Sámuel, 2013-02-13 18:50:40

[1827] Róbert Gida	2013-02-13 20:39:58
Solve[x³-7x+Sqrt*[6]==0,x] a Wolfram Alpha-n.
Előzmény: [1826] w, 2013-02-13 19:11:15

[1826] w	2013-02-13 19:11:15
Keress valamilyen gyököt és gyöktényezőjét emeld ki, ekkor könnyű másodfokú egyenlethez jutsz (sejtéshez nagyon jó egy egyenletmegoldó program, és utólag megállapíthatod, hogy a megfejtéshez nem feltétlenül kell megoldóképlet :-) ).
Előzmény: [1825] Lapis Máté Sámuel, 2013-02-13 18:50:40

[1825] Lapis Máté Sámuel

2013-02-13 18:50:40

Segítsen valaki megoldani ezt a feladatot a harmadfokú egyenlet megoldóképlete nélkül pls.

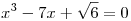
$x^{3}-7x+\sqrt{6}=0$

[1824] koma	2013-02-10 10:32:40
köszönöm szépen
Előzmény: [1823] nadorp, 2013-02-10 10:04:58

[1823] nadorp

2013-02-10 10:04:58

Itt megtalálod a legfontosabbakat.

http://mathworld.wolfram.com/BinomialSeries.html

Előzmény: [1821] koma, 2013-02-09 10:28:06

[1822] Maga Péter	2013-02-09 10:52:24
Nézd meg ezt! Az irányítástartó egybevágóságokról van szó, ami 2 dimenzióban az eltolások és forgatások összessége. A Lie-struktúrát, gondolom, úgy érdemes megadni, hogy az ember beágyazza GL(3)-ba zárt részcsoportként, és örökölteti a 3x3-as mátrixok sokaságstruktúráját.
Előzmény: [1820] Lagrange, 2013-02-09 09:06:11

[1821] koma

2013-02-09 10:28:06

Sziasztok!

A napokban matekozgattam és felmerült egy kérdés bennem Ugyebár mindenki ismeri (a+b)² kifejezést, amikor kifejtjük. Hogy fog ez kinézni pl 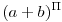$(a+b)^\Pi$ ?

Tehát irracionális kifejezést esetén mi történik? Egy lelkes amatőr vagyok, tehát ha buta kérdés, elnézést kérek...

[1820] Lagrange	2013-02-09 09:06:11
Sziasztok! Valaki meg tudja mondani, hogy az SE(2) melyik Lie csoportot akarja jelenteni? SO(2), SU(2) meg SL(2)-ről hallottam, de ezt még nem sikerült kiderítenem.

[1819] Gizike

2013-02-08 22:00:49

Üdvözlet Mindenkinek!

Tudna valaki segíteni abban, hogy tudok "dobókocka" függvényt készíteni excelben? Nagyon várom a segítséget.

Szép napot!

[1818] Fálesz Mihály	2013-01-16 19:30:58
Gyakorlásképpen számold ki a tg 5 $\alpha$ =0 egyenlettel is.
Előzmény: [1817] Fálesz Mihály, 2013-01-16 19:25:42

[1817] Fálesz Mihály

2013-01-16 19:25:42

Az interneten találsz ilyeneket. http://www.cut-the-knot.org/pythagoras/cos36.shtml

Ha nem ragaszkodsz az elemi megoldáshoz, a tangens addíciós képletével is meg lehet oldani. Például a tg (5 $\alpha$ )=0 vagy a tg (3 $\alpha$ )+tg (2 $\alpha$ )=0 ugyanarra az ötödfokú, de nem túl bonyolult egyenletre vezet, aminek megoldásai 0, $\pm$ tg 36^o és $\pm$ tg 72^o.

Ha t=tg $\alpha$ , akkor $\tg 2\alpha=\frac{2t}{1-t^2}$ , $\tg 3\alpha=\tg(2\alpha+\alpha)= \frac{\frac{2t}{1-t^2}+t}{1-\frac{2t}{1-t^2}t}=\frac{3t-t^3}{1-3t^2}$ , ...

Az egyenlet és megoldása:

tg 2 $\alpha$ +tg 3 $\alpha$ =0

$\frac{2t}{1-t^2} + \frac{3t-t^3}{1-3t^2} =0$

t(t⁴-10t²+5)=0

t=0 vagy $t^2=5\pm2\sqrt{5}$

Minket a kisebbik pozitív gyök érdekel, tehát $\tg36^\circ=\sqrt{5-2\sqrt5}$ .

Előzmény: [1816] Horváth Anett, 2013-01-16 18:30:21

[1816] Horváth Anett

2013-01-16 18:30:21

Sziasztok!

Van egy feladat amit nem tudok megoldani és ehhez szeretnék segítséget kérni: tangens 36 fok pontos értékének a kiszámítása, levezetése.

Előre is köszönöm a segítséget!

[1815] Lóczi Lajos	2012-12-06 08:30:12
Kiindulásul javaslom az alábbi oldalt.
Előzmény: [1814] Hölder, 2012-12-06 00:56:23

[1814] Hölder	2012-12-06 00:56:23
Van egy feladat,amivel nem boldogultam. Ha tudna valaki segíteni, az megköszönném. Igaz -e, hogy minden poliéder gráfjában van Hamilton-kör?

[1813] w	2012-12-03 21:37:43
A válasz kissé pontatlan: A számok: -n, -n+1, -n+2, ..., n-1, n vagy 2n(n+1/2), 2n(n+1/2)+1, ..., 2n(n+3/2)
Előzmény: [1812] w, 2012-12-03 21:34:21

Már regisztráltál?
Új vendég vagy?