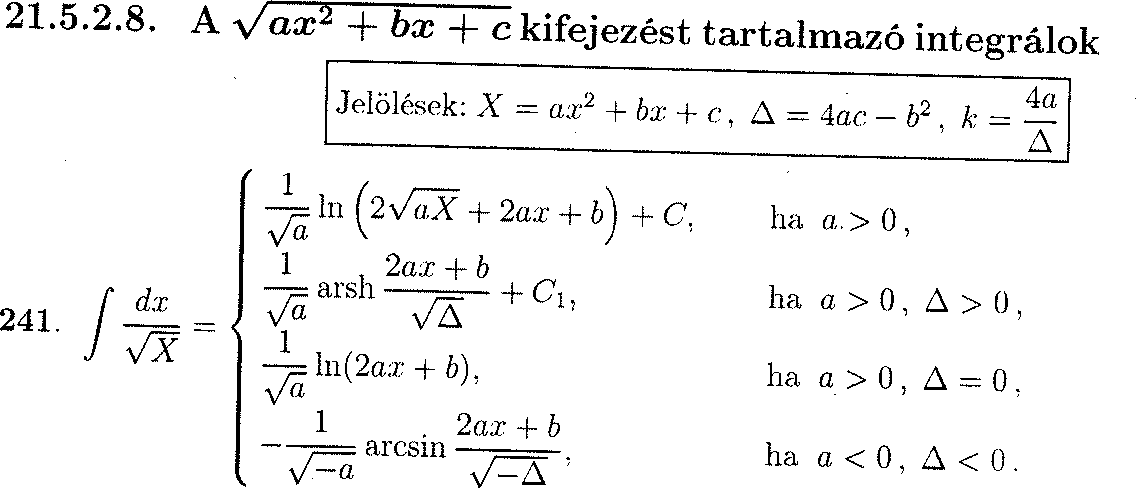| [1845] polarka | 2013-05-06 17:27:43 |
 A logaritmus kezelését úgy gondolom, hogy jelen esetben megkönnyíti az, hogy van egy szabad konstansuk, amit majd a peremfeltétel szab meg. Ezért a komplex logaritmusok közül bármelyiket választva is végül a peremfeltételhez illeszkedő megoldásnál a konstans majd helyretesz mindent.
Igazad van, de a következőképpen egyeznek meg R-ben,  szorzótól eltekintve: szorzótól eltekintve:
![{\rm ar~ch~} \frac{2ax+b}{\sqrt{|\Delta|}}= \ln\left( \frac{2ax+b}{\sqrt{|\Delta|}} + \sqrt{\frac{(2ax+b)^2}{|\Delta|}-1}\right) = \ln\left[\frac{1}{\sqrt{|\Delta|}}\left(2ax+b +\sqrt{(2ax+b)^2-{|\Delta|}}\right)\right] = \ln\left(2ax+b +\sqrt{(2ax+b)^2-{|\Delta|}}\right) + C](keplet.cgi?k=287209BE377E661A)
= az 1. sorral  <0 esetén, ami pedig hasonlóan <0 esetén, ami pedig hasonlóan  -val felírva: -val felírva: 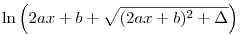 -val egyezik meg. -val egyezik meg.
Azt figyeltem meg, hogy az 1. egyenletben a konstansból behozva 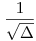 -t arsh ,arch ,arcsin ,arccos is kihozható eredményként, attól függően, hogy "a"-ra és " -t arsh ,arch ,arcsin ,arccos is kihozható eredményként, attól függően, hogy "a"-ra és " "-ra milyen feltételt szabunk. Tehát szerintem az 1. egyenlet általánosabb ilyen tekintetben, mint a többi. "-ra milyen feltételt szabunk. Tehát szerintem az 1. egyenlet általánosabb ilyen tekintetben, mint a többi.
|
| Előzmény: [1842] Fálesz Mihály, 2013-05-06 15:27:29 |
|
|
| [1843] Lóczi Lajos | 2013-05-06 15:47:05 |
 Önmagában egy megoldás attól még nem gyanús, hogy többféle alakban van megadva.
Ha a paramétereket és a változókat komplexnek is megengednék, akkor már ugye a gyökjel sem lenne jóldefiniált, sem a logaritmus, csak némi magyarázkodás után a pontos értelmezési tartományról és értékkészletről.
De ha csak a valós számok között maradunk is, és azt kéred tőlük, hogy tüntessék fel az értelmezési tartományokat, akkor még nem végeztek volna a táblázat összeállításával és nem is férne el a táblázat abban a kötetben, amibe szánták. Pláne, hogy még 3 paraméter is jelen van a példában.
Valamint általános megfigyelés, hogy az ilyesféle táblázatok számtalan hibát tartalmaznak: örülni kell, hogy egyáltalán van valami formula, amit a konkrét alkalmazásban gondosan újra kell értelmezni/bizonyítani.
|
| Előzmény: [1840] polarka, 2013-05-06 12:56:02 |
|
| [1842] Fálesz Mihály | 2013-05-06 15:27:29 |
 Valósban a három eset már az alapintegráloknál is jól megkülönböztethető:
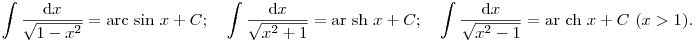
Komplex számokkal a három eset nagyjából ugyanaz, de vigyázni kell arra, hogy a különböző pontokban a végtelen sok logaritmus közül melyiket használod.
A belinkelt szövegben az első sorban szerintem a>0,  <0 kellene. Jó házi feladat, hogy miért nem azt írták azt, hogy <0 kellene. Jó házi feladat, hogy miért nem azt írták azt, hogy  . 1. és a 3. sorban szerintem is hiányzik az abszolútértékjel. A 4. képletet (is) úgy kell érteni, hogy egy olyan intervallumban vagyunk, ahol az integrandus értelmes. . 1. és a 3. sorban szerintem is hiányzik az abszolútértékjel. A 4. képletet (is) úgy kell érteni, hogy egy olyan intervallumban vagyunk, ahol az integrandus értelmes.
De úgysem úszod meg, hogy te magad végigszámold. Ha  =0, akkor a gyökjel alatti kifejezés teljes négyzet. Ha pedig =0, akkor a gyökjel alatti kifejezés teljes négyzet. Ha pedig   0, akkor teljes négyzetté alapítás után egy lineáris helyettesítés vezet a megfelelő alapintegrálra. 0, akkor teljes négyzetté alapítás után egy lineáris helyettesítés vezet a megfelelő alapintegrálra.
|
| Előzmény: [1840] polarka, 2013-05-06 12:56:02 |
|
|
| [1840] polarka | 2013-05-06 12:56:02 |
 Üdv! A következőkben egy integrállal kapcsolatban kérném a segítségeteket.
A bolygómozgással kapcsolatban olvastam és futottam bele az alábbi integrálba (a Bronstejnből szedtem képen látható részletet). Amit olvastam, ott nem részletezte a megoldást, csak közölte arccos-os formában és rejtetten utalt rá, hogy ő is integráltáblázatból szedte.
Viszont én meg nekiálltam, hogy szépen levezessen, mert még nem találkoztam ezzel és gyanús volt, hogy többféle megoldás is lehetne.
Végülis az itt látható mind a 4 megoldást levezettem. Viszont a megszorításokkal és azok értelmezésével bajlódom:
- Én úgy látom, hogy az "a"-ra és " "-ra vonatkozó megkötések azért vannak, hogy ne kerüljenek elő komplex számok. Ezen megkötések tényleg szükségesek? Nem lehetséges az a,b,c,x "-ra vonatkozó megkötések azért vannak, hogy ne kerüljenek elő komplex számok. Ezen megkötések tényleg szükségesek? Nem lehetséges az a,b,c,x C; értelmezéssel mind a 4 kifejezést ekvivalensnek tekinteni? C; értelmezéssel mind a 4 kifejezést ekvivalensnek tekinteni?
- Ha viszont a R halmazán kell maradnunk/akarunk maradni, akkor szerény véleményem szerint az 1. és 3. sorban ln|...| kellene legyen és a 4. sorban pedig szintén megkötést kell tenni az arcsin argumentumára. Mint az enwikin is tették (utolsó előtti szekció eleje).
- Valamint a tetszőleges konstans is hiányzik az utolsó két sorból. Vagy van valami oka ennek, amiről nem tudok?
|
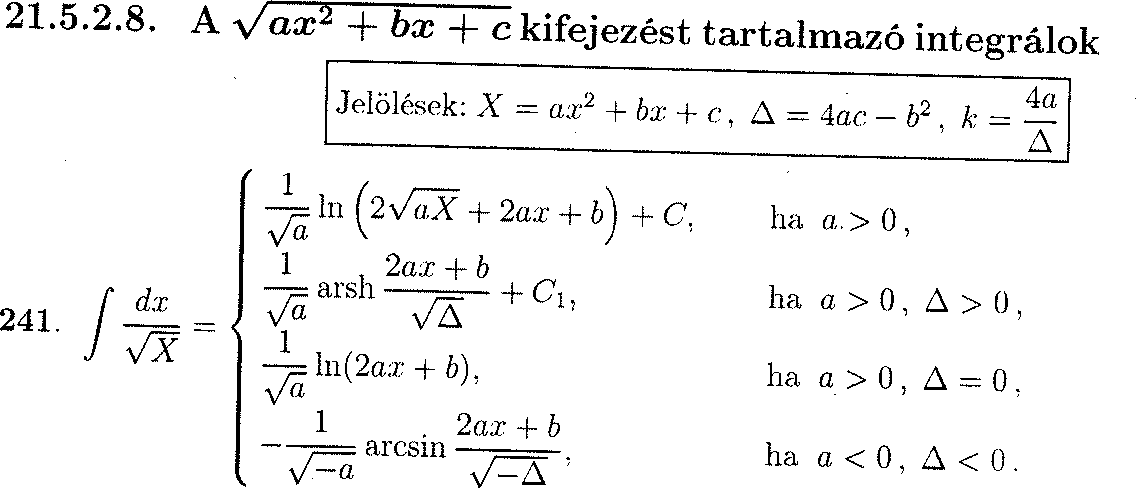 |
|
| [1839] lorantfy | 2013-03-11 21:19:10 |
 Ne izgasd magad ezen! A matematikus BSC-n megtanulod az alapokat. Aztán majd az MSC-n szakosodsz gazdasági matematikára. Ott is szépen levizsgázol mindenből, ami szükséges.
|
| Előzmény: [1838] koma, 2013-03-10 21:52:21 |
|
| [1838] koma | 2013-03-10 21:52:21 |
 Sziasztok!
Lenne egy meglehetősen furcsa kérdésem: Hogyan lesz valakiből jó pénzügyi matematikus?
Ez nagyon furcsán hangzik, de leírom, hogy mire gondolok. Én matematika szakon szeretném folytatni a tanulmányaimat szept-től és nem látom, hogy milyen mélységig kell az egyes területekben elmélyedni? Annyira szerteágazó a matematika és rengeteg szakkönyv van, hogy félelmetes. Például nekem mennyire kell értenem a számelmélethez ahhoz, hogy ezen a területen dolgozhassak? Én szeretnék jó szakember lenni, de még így is a szakterületen belül rengeteg könyvet találtam például sztochasztikus-differenciálterületekről. Ezek a könyvek azért többnyire átfedésben lehetnek?
Megnyugtató válaszaitokat előre is köszönöm!:)
|
|
|
|
| [1835] koma | 2013-02-25 07:48:52 |
 Sziasztok!
Valaki meg tudná esetleg mondani, hogy a "többváltozós függvények" kifejezést hogyan mondják angolul illetve németül?
Köszönöm a segítséget!:)
|
|
|
|
|
| [1831] Kőrösi Ákos | 2013-02-22 16:47:07 |
 Legyen adott egy természetes számokból képzett végtelen sorozat. Van-e olyan algoritmus, mely eldönti a sorozat reciprokösszegét?
|
|
|
|
|
|
|
| [1825] Lapis Máté Sámuel | 2013-02-13 18:50:40 |
 Segítsen valaki megoldani ezt a feladatot a harmadfokú egyenlet megoldóképlete nélkül pls.
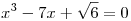
|
|
|
|
| [1822] Maga Péter | 2013-02-09 10:52:24 |
 Nézd meg ezt! Az irányítástartó egybevágóságokról van szó, ami 2 dimenzióban az eltolások és forgatások összessége. A Lie-struktúrát, gondolom, úgy érdemes megadni, hogy az ember beágyazza GL(3)-ba zárt részcsoportként, és örökölteti a 3x3-as mátrixok sokaságstruktúráját.
|
| Előzmény: [1820] Lagrange, 2013-02-09 09:06:11 |
|
| [1821] koma | 2013-02-09 10:28:06 |
 Sziasztok!
A napokban matekozgattam és felmerült egy kérdés bennem Ugyebár mindenki ismeri (a+b)2 kifejezést, amikor kifejtjük. Hogy fog ez kinézni pl 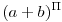 ? ?
Tehát irracionális kifejezést esetén mi történik? Egy lelkes amatőr vagyok, tehát ha buta kérdés, elnézést kérek...
|
|



 <0 esetén, ami pedig hasonlóan
<0 esetén, ami pedig hasonlóan 

 0, akkor teljes négyzetté alapítás után egy lineáris helyettesítés vezet a megfelelő alapintegrálra.
0, akkor teljes négyzetté alapítás után egy lineáris helyettesítés vezet a megfelelő alapintegrálra. 
 C; értelmezéssel mind a 4 kifejezést ekvivalensnek tekinteni?
C; értelmezéssel mind a 4 kifejezést ekvivalensnek tekinteni?