| [1867] Lóczi Lajos | 2013-05-23 15:00:42 |
 De ebben az esetben pontosan ezt gondolom. A HK-integrál éppoly természetes, ha vki először hallja, és nem csak elsős matematikusokra gondolok. A mögöttes tartalom pedig csupán annyi, hogy ha a függvény valahol csúnyán változik, akkor a téglalapos közelítőösszegeket is ennek megfelelően finomítsuk: egy igazi adaptív algoritmus.
|
| Előzmény: [1866] Micimackó, 2013-05-23 09:26:00 |
|
| [1866] Micimackó | 2013-05-23 09:26:00 |
 Nem gondolhatod, hogy matematikában csak mert két dolog definíciója pofára hasonló, hasonlóan nehéz lesz megérteni a fogalmakat :) A Riemann integrál egy elsős matematikus számára könnyen érthető és természetes, míg ezen igen csak törnie kéne a fejét, és nem is biztos hogy rendesen megértené miről is van szó (és így az egész csak formális zúzás lenne neki).
|
| Előzmény: [1865] Lóczi Lajos, 2013-05-14 23:49:32 |
|
| [1865] Lóczi Lajos | 2013-05-14 23:49:32 |
 Csak 1-2 morzsát írok, a többit az idézett oldalakon megadott összefoglaló könyvekből jól áttekintheted egy kis kutatómunka után.
Rejtély számomra, hogy a Henstock--Kurzweil-integrál (HK) miért nem vette át pl. az egyetemi tananyagban a Riemann-integrál helyét: a definíciók közötti különbség alig észrevehető, a nyereség viszont nagy. Ki és miért ennyire konzervatív?
A HK-integrál egyik hátránya, hogy (alapesetben) csak intervallumokon tudunk vele integrálni. Egy másik hátránya, hogy a HK-integrálható függvények tere nem teljes.
A Lebesgue-integrál (L) esetében a fenti teljesség teljesül: ez az alkalmazásokban döntően fontos tényező, ami a mérleget itt az L-integrál javára billenti. Az L-integrállal bonyolult halmazokon is lehet integrálni. Ezt az integrálfogalmat a valós számok halmazánál absztraktabb terekre könnyű kiterjeszteni.
A különféle integrálfogalmak fejlődését az alkalmazások motiválták: egy fontos elméleti/gyakorlati kérdés alapos tanulmányozásakor sokszor kifejlesztettek egy új integrálfogalmat.
Az idézett oldalon felsorolt integrálfogalmak nem feltétlenül összehasonlíthatók Venn-diagramon: más típusú (máshol értelmezett/más típusú térbe képező) függvényekre vannak kitalálva.
|
| Előzmény: [1864] polarka, 2013-05-14 10:08:02 |
|
| [1864] polarka | 2013-05-14 10:08:02 |
 Köszi.
Nézegettem az enwikin és huwikin, hogy azért van bőven egyéb, Riemann-tól eltérő integrál definíció. Elolvastam az enwiki: Henstock-Kurzweil integral cikket, ahol azt állítják, hogy általánosabb, több függvényre használható, mint a Lebesgue-integrál, ami pedig a Riemann kiterjesztése.
A kérdésem az, hogy mi az oka annak, hogy ha már adott egy olyan értelmezés, ahol az eddig is értelmezett integrálokat ugyanúgy lehet számolni, mint eddig és értelmet ad olyan integráloknak, amelyeket addig nem tudtunk értelmezni és mégsem az az alapértelmezettnek vett integrál definíció, miért nem azt tanítják?
Nem tudsz egy Venn-diagramos vagy hierarchiás fa-gráfos összefoglalót az összes integrál-definícióval és azok kapcsolatairól? Egy ilyen ábrán azonnal látszódnának bárkinek hogy hogyan viszonyulnak egymáshoz, anélkül hogy végigolvasná őket egyenként és saját maga építené fel a fejében a kapcsolatokat.
|
| Előzmény: [1863] Lóczi Lajos, 2013-05-11 16:36:54 |
|
| [1863] Lóczi Lajos | 2013-05-11 16:36:54 |
 Természetesen értelmezhető az ilyen "+ - - -típusú" integrál szimmetrikus módon is, ahogyan írtad, ezt hívják Cauchy-féle főértéknek, és pl. a -típusú" integrál szimmetrikus módon is, ahogyan írtad, ezt hívják Cauchy-féle főértéknek, és pl. a 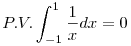 szimbólummal jelöljük. szimbólummal jelöljük.
De ha a közönséges, (improprius értelemben vett) Riemann-integrálról van szó, akkor a szóban forgó 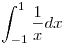 kifejezést nem definiáljuk. kifejezést nem definiáljuk.
Mindezzel csak arra szerettem volna rámutatni, hogy milyen nehéz vállalkozás igazi, "felhasználóbarát" határozatlanintegrál-táblázatot csinálni: a felhasználó ki szeretne számolni egy 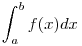 határozott integrált, mint pl. az [1840]-es hozzászólásban szereplő háromparaméteres kifejezést, úgy, hogy csak be kelljen helyettesítenie az F(b)-F(a) képletbe, és ne neki (hanem a táblázat készítőjének) kelljen azzal törődnie, hogy a képlet helyes eredményt adjon, figyeljen az értelmezési tartományokra, vagy hogy pl. fellép-e a fent is említett + határozott integrált, mint pl. az [1840]-es hozzászólásban szereplő háromparaméteres kifejezést, úgy, hogy csak be kelljen helyettesítenie az F(b)-F(a) képletbe, és ne neki (hanem a táblázat készítőjének) kelljen azzal törődnie, hogy a képlet helyes eredményt adjon, figyeljen az értelmezési tartományokra, vagy hogy pl. fellép-e a fent is említett + - - eset. eset.
|
| Előzmény: [1861] polarka, 2013-05-09 15:43:41 |
|
|
| [1861] polarka | 2013-05-09 15:43:41 |
 Két különböző területet számoltunk. Nem ugyanazt kétféleképpen.
Azon részével "nem értek egyet", hogy az egyik határt  -nak, a másikat meg 2 -nak, a másikat meg 2 -nak határoztad meg. Én alapértelmezetten azonosnak venném a kettőt. Szimmetrikusan kezelném a területszámítást, ameddig egy adott konkrét példánál elő nem kerülne, hogy a két oldalon más-más határnál szűnik meg az 1/x-es függés. Mert ugye egy ilyet csak konkrét határok figyelembevételével lehetne kiértékelni. Ezen utosó mondatomból is következik, hogy a processzor tudja, hogy milyen értékre számol területet, vagy ha csak elkezdi a vakvilágba, akkor is tudja számolni, hogy hányadik lépésnél tart, ergo a két proci össze tudja hasonlítani, hogy melyikőjük hol tart. -nak határoztad meg. Én alapértelmezetten azonosnak venném a kettőt. Szimmetrikusan kezelném a területszámítást, ameddig egy adott konkrét példánál elő nem kerülne, hogy a két oldalon más-más határnál szűnik meg az 1/x-es függés. Mert ugye egy ilyet csak konkrét határok figyelembevételével lehetne kiértékelni. Ezen utosó mondatomból is következik, hogy a processzor tudja, hogy milyen értékre számol területet, vagy ha csak elkezdi a vakvilágba, akkor is tudja számolni, hogy hányadik lépésnél tart, ergo a két proci össze tudja hasonlítani, hogy melyikőjük hol tart.
Szerintem a megoldás: Vagy jelöljük mindig konkrétan, hogy mit értünk alatta vagy elfogadunk egy értelmezést alapértelmezettnek és a többit jelöljük külön. (Szerintem a szimmetrikus eléggé adja magát.)
|
| Előzmény: [1860] Lóczi Lajos, 2013-05-07 17:23:59 |
|
| [1860] Lóczi Lajos | 2013-05-07 17:23:59 |
 Az nem lenne jó, ha itt mindkettőnknek igaza lenne és a területet kétféleképpen is lehetne definiálni.
Konkrétan, melyik részlépéssel nem értesz egyet a levezetésemben? Továbbá képzeljük azt, hogy az egyik processzor a bal oldali területet számolja ki, a másik pedig a jobb oldalit: az egyik nem tud arról, hogy a másik "ugyanannyira közelíti-e a 0-t".
Mi legyen a megoldás?
|
| Előzmény: [1859] polarka, 2013-05-07 17:18:23 |
|
| [1859] polarka | 2013-05-07 17:18:23 |
 Mindkettőnknek!?
Az nyilván igaz, hogy [-1,0) között a fv -1 szerese a (0,1] közötti részének, tehát előjeles összegük 0-ra kell kijöjjön, ha ugyanannyira közelíted a 0-t mindkét oldalról. Ha pedig a feltétel nem teljesül, akkor nyilván nem lesz 0.
|
| Előzmény: [1858] Lóczi Lajos, 2013-05-07 16:53:33 |
|
|
|
| [1856] Lóczi Lajos | 2013-05-07 16:13:32 |
 Egyetértek, a cél nyilván az, hogy ezeket a formulákat pl. területszámításra használjuk. De akkor meg kell kérdezzem, hogy a korábbi c1=c2=c választással kapott primitívfüggvény-sereg megfelel-e a területszámítási intuíciónknak:
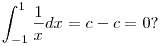
Vagyis ebben a példában a szimmetrikus területet valóban 0-nak szeretnénk definiálni?
|
| Előzmény: [1855] polarka, 2013-05-07 16:06:46 |
|
| [1855] polarka | 2013-05-07 16:06:46 |
 Talán, mert ha majdan függvény alatti területként szeretné valaki használni, akkor a következő határozott integrált kapnánk 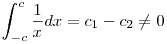 , ahol c , ahol c R+ R+
Ami nem felelne meg a területszámítási intuíciónak.
|
| Előzmény: [1854] Lóczi Lajos, 2013-05-07 15:17:27 |
|
| [1854] Lóczi Lajos | 2013-05-07 15:17:27 |
 Akkor -- továbbra is csak a valós számok körében maradva -- azt kérdezném, hogy mi az oka annak, hogy számos integráltáblázatban azt látom, amit írtál, miszerint
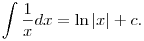
Azt írod, hogy az értelmezési tartomány legyen a maximális, azaz a 0-tól különböző valósok halmaza. Ha lerajzoljuk ezeket a függvényeket, akkor látszik, hogy mind tengelyesen szimmetrikusak. Én mondok egy bővebb függvényosztályt eredményül:
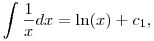
ha x>0, és
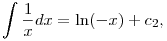
ha x<0. Vagyis itt a két ág függőleges eltolása már nem feltétlenül ugyanaz.
Miért nem ezt a bővebb osztályt szokták akkor a könyvek feltüntetni?
|
| Előzmény: [1851] polarka, 2013-05-07 10:52:50 |
|
| [1853] polarka | 2013-05-07 11:56:53 |
 De ezen értékek csak a képzetes részt befolyásolják. Nem látom, hogy miért lenne probléma, ha tudok arról is, hogy az illető milyen úton (jelen esetben hányszor kerüli meg az origót és mekkora két pont közötti szögtávolság).
Mert én úgy látom, hogy az integrál felfogható úgy mint, egy vektor-vektor fv-ben végzett mozgás során végzett vonalintegrál. Ahol a valós rész a szokásos skalárszorzatot, a képzetes rész pedig a vektoriális szorzat értékét hordozza.
|
| Előzmény: [1852] Alma, 2013-05-07 10:58:12 |
|
| [1852] Alma | 2013-05-07 10:58:12 |
 Az a probléma (határozott integrálban gondolkodva), hogy míg valósban két szám között csak egyféle szakaszon tudsz integrálni (a valós tengely megfelelő részén), a komplex síkon két számot különböző görbékkel tudsz összekötni. Így c1 és c2 közötti határozott integrált több különböző görbén is értelmezheted, és sajnos ezek bizonyos függvényeknél különböző értékeket adhatnak. Ha a függvényednek nincs pólusa, akkor a különböző görbéken elvégzett integrálok értékei megegyeznek. Az 1/x függvénynek van pólusa x=0-ban.
|
| Előzmény: [1851] polarka, 2013-05-07 10:52:50 |
|
|
|
| [1849] Lóczi Lajos | 2013-05-07 07:01:45 |
 Ne szaladj ennyire előre :) Egyelőre csak a valós számok körében akarjunk dolgozni, akárcsak korábban. De kérlek, ne csak formulákat írj, hanem az általuk meghatározott függvények értelmezési tartományait is tüntesd fel.
|
| Előzmény: [1848] polarka, 2013-05-06 23:47:03 |
|
|
|
| [1846] polarka | 2013-05-06 17:47:25 |
 Nem a megoldás volt gyanús, hanem azon kezdtem gyanakodni, hogy ebben az integrálban azért több van, mint amit a bolygómozgásnál közöltek és be is igazolódott, hogy azért mégsem olyan egyszerű és volna még mit diszkutálni róla, hogy minden világos legyen. Ott csak közöltek egy megoldást, ami azért ránézésből egyáltalán nem volt triviális (ott még ez az egyszerűbb alak sem volt leírva).
Elfogadom én, hogy valós számokról van ott szó. A kérdésem arra irányul, hogy minden egyes feltétel csak azért van, hogy ez stimmeljen és nem lehetne egy megoldást felírni, amiből tovább vezetve egyéb feltételekkel, diszkusszióval megkaphatóak, amik ott szerepelnek. Mivel én úgy látom, hogy az elsőből a többi következik (azt hiszem a 3. kivételével, de lehet arról is beláttam már, hogy mégis?), ezért úgy érzem, hogy elég volna az elsőt közölni, mint megoldást. És a többit meg jelezvén, hogy azon megoldás diszkutálása bizonyos feltételek mellett és nem pedig egyenrangú megoldások. De lehet tévedek, ezért is kértem a segítségetek.
Igen, ezt én is megfigyeltem, de ha találok hibát, akkor azt legalább a sajátomban átjavítom vagy bővítem, hogy világosabb legyen, hogy ott miről is van szó. Egyszer az elejétől nekiláttam ennek, míg bele nem untam és találtam bőven elgépeléseket. Vagy nagyon nem intuitív jelöléseket.
|
| Előzmény: [1843] Lóczi Lajos, 2013-05-06 15:47:05 |
|
| [1845] polarka | 2013-05-06 17:27:43 |
 A logaritmus kezelését úgy gondolom, hogy jelen esetben megkönnyíti az, hogy van egy szabad konstansuk, amit majd a peremfeltétel szab meg. Ezért a komplex logaritmusok közül bármelyiket választva is végül a peremfeltételhez illeszkedő megoldásnál a konstans majd helyretesz mindent.
Igazad van, de a következőképpen egyeznek meg R-ben,  szorzótól eltekintve: szorzótól eltekintve:
![{\rm ar~ch~} \frac{2ax+b}{\sqrt{|\Delta|}}= \ln\left( \frac{2ax+b}{\sqrt{|\Delta|}} + \sqrt{\frac{(2ax+b)^2}{|\Delta|}-1}\right) = \ln\left[\frac{1}{\sqrt{|\Delta|}}\left(2ax+b +\sqrt{(2ax+b)^2-{|\Delta|}}\right)\right] = \ln\left(2ax+b +\sqrt{(2ax+b)^2-{|\Delta|}}\right) + C](keplet.cgi?k=287209BE377E661A)
= az 1. sorral  <0 esetén, ami pedig hasonlóan <0 esetén, ami pedig hasonlóan  -val felírva: -val felírva: 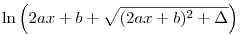 -val egyezik meg. -val egyezik meg.
Azt figyeltem meg, hogy az 1. egyenletben a konstansból behozva 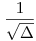 -t arsh ,arch ,arcsin ,arccos is kihozható eredményként, attól függően, hogy "a"-ra és " -t arsh ,arch ,arcsin ,arccos is kihozható eredményként, attól függően, hogy "a"-ra és " "-ra milyen feltételt szabunk. Tehát szerintem az 1. egyenlet általánosabb ilyen tekintetben, mint a többi. "-ra milyen feltételt szabunk. Tehát szerintem az 1. egyenlet általánosabb ilyen tekintetben, mint a többi.
|
| Előzmény: [1842] Fálesz Mihály, 2013-05-06 15:27:29 |
|
|
| [1843] Lóczi Lajos | 2013-05-06 15:47:05 |
 Önmagában egy megoldás attól még nem gyanús, hogy többféle alakban van megadva.
Ha a paramétereket és a változókat komplexnek is megengednék, akkor már ugye a gyökjel sem lenne jóldefiniált, sem a logaritmus, csak némi magyarázkodás után a pontos értelmezési tartományról és értékkészletről.
De ha csak a valós számok között maradunk is, és azt kéred tőlük, hogy tüntessék fel az értelmezési tartományokat, akkor még nem végeztek volna a táblázat összeállításával és nem is férne el a táblázat abban a kötetben, amibe szánták. Pláne, hogy még 3 paraméter is jelen van a példában.
Valamint általános megfigyelés, hogy az ilyesféle táblázatok számtalan hibát tartalmaznak: örülni kell, hogy egyáltalán van valami formula, amit a konkrét alkalmazásban gondosan újra kell értelmezni/bizonyítani.
|
| Előzmény: [1840] polarka, 2013-05-06 12:56:02 |
|





 -
- -nak, a másikat meg 2
-nak, a másikat meg 2 R+
R+  C, így amit leírtam
C, így amit leírtam  =0 vagy
=0 vagy  (+k2
(+k2 )-vel adódik:
)-vel adódik: 

 0-ra is.
0-ra is.