|
| [1878] koma | 2013-09-28 18:59:33 |
 Sziasztok, akadt két problémám, nagyon megköszönném, ha valaki kisegítene.:)
1, Határozza meg az a1=1,an+1=2an (n term szám) rekurzív sorozat képletét.
2,Mutassuk meg, hogy az alábbi rekurzív sorozat monoton csökkenő: a1=2,a2=1,an+1=5an-6an-1,(n 2) 2)
köszönöm szépen a segítséget.
|
|
| [1877] bianka | 2013-09-28 10:25:42 |
 szia!
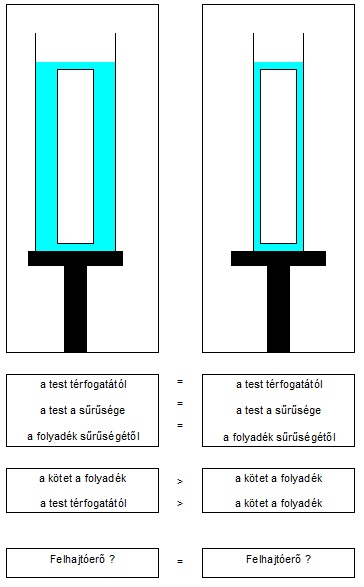
egy gyors kérdés (skicc)
köszi! ...bianka
|
 |
|
| [1876] gyula60 | 2013-09-17 20:11:06 |
 Javaslom az 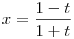 helyettesítés alkalmazását, amely után a kanonikus alakra hozás jobban megvalósítható. helyettesítés alkalmazását, amely után a kanonikus alakra hozás jobban megvalósítható.
A keresett primitív fügvényt a következő két f1(x) és f2(x) függvény összege állítja elő:
![f_1(x)=-\frac{1}{\sqrt2}arc\tg\bigg[\frac{\root\of{x^2+x+1}}{\sqrt2(x-1)}\bigg]](keplet.cgi?k=7F83EA544685A758) , ,
![f_2(x)=-\frac{1}{\sqrt6}\ln\bigg[\frac{\sqrt2(x+1)-\root\of{3(x^2+x+1)}}{\root\of{(x^2-x+1)}}\bigg]](keplet.cgi?k=B1C572E2B7464A7A) . .
|
| Előzmény: [1874] juantheron, 2013-09-02 21:12:42 |
|
|
|
| [1873] Lóczi Lajos | 2013-05-24 15:17:24 |
 Kedves Mihály,
szerintem érdemes elkülöníteni a különböző célcsoportokat.
A gyakorlatban előkerülő szakaszonként sima függvények integrálásához mindenki a Newton--Leibniz-formulát fogja akarni használni; ez a célcsoport nem akar Dirichlet-függvényt integrálni, vagy bármit az integrál definíciója alapján kiszámítani. A HK-elmélet keretében a Newton--Leibniz-tételkör nagyon természetes módon tárgyalható, ami nem mondható el a Riemann- vagy a Lebesgue-elméletről. Ez a célcsoport nem fog semmilyen  függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet. függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet.
Egy következő célcsoport lehet az, akik látják, hogy van pl. Dirichlet-függvény, és ezt konstans  -val nem lehet integrálni (azaz Riemann-értelemben), de egy kicsit bonyolultabb -val nem lehet integrálni (azaz Riemann-értelemben), de egy kicsit bonyolultabb  -val már lehet. Ha e célcsoport tagjai ezt a -val már lehet. Ha e célcsoport tagjai ezt a  függvényt bonyolultnak találják, akkor nekik a Lebesgue-elmélet sem lenne emészthető. De itt sem muszáj a "definíció" szerinti integrálást erőltetni, a Dirichlet-fv. integráljának értéke a tételekből úgyis "kijön". függvényt bonyolultnak találják, akkor nekik a Lebesgue-elmélet sem lenne emészthető. De itt sem muszáj a "definíció" szerinti integrálást erőltetni, a Dirichlet-fv. integráljának értéke a tételekből úgyis "kijön".
Aki pedig absztrakt Lebesgue-elméletet akar tanulni, annak -- a Lebesgue-elmélet megismerése előtt -- nagyon tanulságos lehet látni, hogy milyen gyorsan el lehet jutni egy [a,b]-n értelmezett függvény integráljának definíciójához, amit később majd Lebesgue-integrálnak fogunk hívni és egy bonyolultabb apparátus keretében absztraktabban és általánosabban felépíteni.
|
| Előzmény: [1872] Fálesz Mihály, 2013-05-24 10:34:11 |
|
| [1872] Fálesz Mihály | 2013-05-24 10:34:11 |
 Kedves Lajos,
A kérdésed az volt, hogy a HK integrál miért nem vette át pl. az egyetemi tananyagban a Riemann-integrál helyét.
Több okot is látok. Az egyik didaktikai. Én legalábbi személy jobban szeretem, ha a világot apránként fedezzük fel. Előbb találunk néhány mozaikdarabot, ezeket tanulmányozzuk, emésztjük, és csak utána építünk fel valami általánosabb rendszert, aminek a sok darab mind része. Számomra mindig elrettentő példát jelentenek az olyan esetek, ahol előbb kimondanak és bebizonyítanak egy nagyon absztrakt tételt, és utána ennek speciális esete lesz a többi, külön-külön sokkal érdekesebb állítás.
A másik ok, hogy nem akarunk túl sok fölösleges dolgot tanítani. Egy mérnök vagy egy alkalmazott matematikus szép, szakaszonként sima függvényekkel dolgozik, és valószínűleg soha nem akarja mondjuk a Dirichlet-függvényt integrálni. Nekik bőven elég az (improprius) Riemann-integrál, és az x2 integrálása sem okoz túl nagy traumát egyenletes felosztással. Semmi nyereség nincs mindaddig, amíg csak véges sok pont közelében van gond a függvénnyel. Az improprius integrált (végtelen inervallumokon) úgysem ússzuk meg.
Azt is írtad, hogy a definíciók közötti különbség alig észrevehető, a nyereség viszont nagy.
Az alig észrevehető különbség valójában óriási. Persze, mondhatjuk ártatlan arccal, hogy konstans  helyett inkább egy pozitív értékű függvényt veszünk, de ez félrevezető. A többség valami viszonylag szép helyett inkább egy pozitív értékű függvényt veszünk, de ez félrevezető. A többség valami viszonylag szép  függvényt fog várni, tévesen. Nehezen fogják megemészteni azt a sokkot, hogy a várt szakaszonként folytonos függvény helyett miféle szörnyűségekbe ütközhetnek; hogy egy kicsit csúnyább függvény (pl. a Dirichlet-függvény) integrálásához mennyire bonyolult függvényt fog várni, tévesen. Nehezen fogják megemészteni azt a sokkot, hogy a várt szakaszonként folytonos függvény helyett miféle szörnyűségekbe ütközhetnek; hogy egy kicsit csúnyább függvény (pl. a Dirichlet-függvény) integrálásához mennyire bonyolult  függvényt érdemes választani. függvényt érdemes választani.
Ha pedig elkezdjük vizsgálni, hogy egyes függvények miért (nem) HK integrálhatók, óhatalanul beleütközünk a Lebesgue-mérték hiányába. Ezért gondolom, hogy a HK integrállal a mértékelmélet után érdmes foglalkozni.
|
| Előzmény: [1870] Lóczi Lajos, 2013-05-23 22:23:19 |
|
| [1871] Lóczi Lajos | 2013-05-23 23:58:10 |
 Szerintem az alapvető tételek bizonyításai nem nehezebbek, lásd pl. Lee Peng-Yee: Lanzhou Lectures on Henstock Integration c. művét 1989-ből, amely a fogalom felépítésére koncentrál.
Vagy érdemes egy pillantást vetni erre a masszívabb könyvre Brian S. Thomson: Theory of the integral, amely összehasonlító szempontból tárgyal viszonylag sok integrálfogalmat.
De hogy a Riemann-integrál fogalma is rejteget még nemtriviális részleteket: 2009-ben adták meg annak szükséges és elégséges feltételét, hogy egy F függvény előálljon, mint egy f Riemann-integrálható függvény integrálfüggvénye. Azaz: mik a feltételek F-re, hogy létezzen hozzá egy c konstans és f Riemann-integrálható függvény, hogy 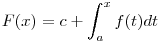 legyen (x legyen (x [a,b]). [a,b]).
|
| Előzmény: [1868] jonas, 2013-05-23 15:10:52 |
|
| [1870] Lóczi Lajos | 2013-05-23 22:23:19 |
 Ahhoz mennyi előkészületre van szükség (a definíciókkal együtt), hogy az x x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon? x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon?
Véleményem szerint ennél kevesebb vesződséggel jár a Dirichlet-függvényről megmutatni a definíciókból, hogy HK-integrálja 0.
Ha nem cél az absztrakt mértékelmélet tanulmányozása, a HK-integrál fogalma kifizetődőbben felépíthető, mint a Lebesgue-integrálé.
|
| Előzmény: [1869] Fálesz Mihály, 2013-05-23 17:09:02 |
|
| [1869] Fálesz Mihály | 2013-05-23 17:09:02 |
 Szerintem nem olyan egyszerű ez az integrálfogalom, és inkább a mértékelmélet tárgyalása után érdemes foglalkozni vele.
Például próbáljuk integrálni a Dirichlet-függvényt, vagy a Cantor halmaz összes racionális eltoltja uniójának karakterisztikus függvényét a [0,1] intervallumban.
|
| Előzmény: [1865] Lóczi Lajos, 2013-05-14 23:49:32 |
|
|
| [1867] Lóczi Lajos | 2013-05-23 15:00:42 |
 De ebben az esetben pontosan ezt gondolom. A HK-integrál éppoly természetes, ha vki először hallja, és nem csak elsős matematikusokra gondolok. A mögöttes tartalom pedig csupán annyi, hogy ha a függvény valahol csúnyán változik, akkor a téglalapos közelítőösszegeket is ennek megfelelően finomítsuk: egy igazi adaptív algoritmus.
|
| Előzmény: [1866] Micimackó, 2013-05-23 09:26:00 |
|
| [1866] Micimackó | 2013-05-23 09:26:00 |
 Nem gondolhatod, hogy matematikában csak mert két dolog definíciója pofára hasonló, hasonlóan nehéz lesz megérteni a fogalmakat :) A Riemann integrál egy elsős matematikus számára könnyen érthető és természetes, míg ezen igen csak törnie kéne a fejét, és nem is biztos hogy rendesen megértené miről is van szó (és így az egész csak formális zúzás lenne neki).
|
| Előzmény: [1865] Lóczi Lajos, 2013-05-14 23:49:32 |
|
| [1865] Lóczi Lajos | 2013-05-14 23:49:32 |
 Csak 1-2 morzsát írok, a többit az idézett oldalakon megadott összefoglaló könyvekből jól áttekintheted egy kis kutatómunka után.
Rejtély számomra, hogy a Henstock--Kurzweil-integrál (HK) miért nem vette át pl. az egyetemi tananyagban a Riemann-integrál helyét: a definíciók közötti különbség alig észrevehető, a nyereség viszont nagy. Ki és miért ennyire konzervatív?
A HK-integrál egyik hátránya, hogy (alapesetben) csak intervallumokon tudunk vele integrálni. Egy másik hátránya, hogy a HK-integrálható függvények tere nem teljes.
A Lebesgue-integrál (L) esetében a fenti teljesség teljesül: ez az alkalmazásokban döntően fontos tényező, ami a mérleget itt az L-integrál javára billenti. Az L-integrállal bonyolult halmazokon is lehet integrálni. Ezt az integrálfogalmat a valós számok halmazánál absztraktabb terekre könnyű kiterjeszteni.
A különféle integrálfogalmak fejlődését az alkalmazások motiválták: egy fontos elméleti/gyakorlati kérdés alapos tanulmányozásakor sokszor kifejlesztettek egy új integrálfogalmat.
Az idézett oldalon felsorolt integrálfogalmak nem feltétlenül összehasonlíthatók Venn-diagramon: más típusú (máshol értelmezett/más típusú térbe képező) függvényekre vannak kitalálva.
|
| Előzmény: [1864] polarka, 2013-05-14 10:08:02 |
|
| [1864] polarka | 2013-05-14 10:08:02 |
 Köszi.
Nézegettem az enwikin és huwikin, hogy azért van bőven egyéb, Riemann-tól eltérő integrál definíció. Elolvastam az enwiki: Henstock-Kurzweil integral cikket, ahol azt állítják, hogy általánosabb, több függvényre használható, mint a Lebesgue-integrál, ami pedig a Riemann kiterjesztése.
A kérdésem az, hogy mi az oka annak, hogy ha már adott egy olyan értelmezés, ahol az eddig is értelmezett integrálokat ugyanúgy lehet számolni, mint eddig és értelmet ad olyan integráloknak, amelyeket addig nem tudtunk értelmezni és mégsem az az alapértelmezettnek vett integrál definíció, miért nem azt tanítják?
Nem tudsz egy Venn-diagramos vagy hierarchiás fa-gráfos összefoglalót az összes integrál-definícióval és azok kapcsolatairól? Egy ilyen ábrán azonnal látszódnának bárkinek hogy hogyan viszonyulnak egymáshoz, anélkül hogy végigolvasná őket egyenként és saját maga építené fel a fejében a kapcsolatokat.
|
| Előzmény: [1863] Lóczi Lajos, 2013-05-11 16:36:54 |
|
| [1863] Lóczi Lajos | 2013-05-11 16:36:54 |
 Természetesen értelmezhető az ilyen "+ - - -típusú" integrál szimmetrikus módon is, ahogyan írtad, ezt hívják Cauchy-féle főértéknek, és pl. a -típusú" integrál szimmetrikus módon is, ahogyan írtad, ezt hívják Cauchy-féle főértéknek, és pl. a 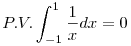 szimbólummal jelöljük. szimbólummal jelöljük.
De ha a közönséges, (improprius értelemben vett) Riemann-integrálról van szó, akkor a szóban forgó 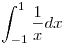 kifejezést nem definiáljuk. kifejezést nem definiáljuk.
Mindezzel csak arra szerettem volna rámutatni, hogy milyen nehéz vállalkozás igazi, "felhasználóbarát" határozatlanintegrál-táblázatot csinálni: a felhasználó ki szeretne számolni egy 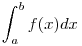 határozott integrált, mint pl. az [1840]-es hozzászólásban szereplő háromparaméteres kifejezést, úgy, hogy csak be kelljen helyettesítenie az F(b)-F(a) képletbe, és ne neki (hanem a táblázat készítőjének) kelljen azzal törődnie, hogy a képlet helyes eredményt adjon, figyeljen az értelmezési tartományokra, vagy hogy pl. fellép-e a fent is említett + határozott integrált, mint pl. az [1840]-es hozzászólásban szereplő háromparaméteres kifejezést, úgy, hogy csak be kelljen helyettesítenie az F(b)-F(a) képletbe, és ne neki (hanem a táblázat készítőjének) kelljen azzal törődnie, hogy a képlet helyes eredményt adjon, figyeljen az értelmezési tartományokra, vagy hogy pl. fellép-e a fent is említett + - - eset. eset.
|
| Előzmény: [1861] polarka, 2013-05-09 15:43:41 |
|
|
| [1861] polarka | 2013-05-09 15:43:41 |
 Két különböző területet számoltunk. Nem ugyanazt kétféleképpen.
Azon részével "nem értek egyet", hogy az egyik határt  -nak, a másikat meg 2 -nak, a másikat meg 2 -nak határoztad meg. Én alapértelmezetten azonosnak venném a kettőt. Szimmetrikusan kezelném a területszámítást, ameddig egy adott konkrét példánál elő nem kerülne, hogy a két oldalon más-más határnál szűnik meg az 1/x-es függés. Mert ugye egy ilyet csak konkrét határok figyelembevételével lehetne kiértékelni. Ezen utosó mondatomból is következik, hogy a processzor tudja, hogy milyen értékre számol területet, vagy ha csak elkezdi a vakvilágba, akkor is tudja számolni, hogy hányadik lépésnél tart, ergo a két proci össze tudja hasonlítani, hogy melyikőjük hol tart. -nak határoztad meg. Én alapértelmezetten azonosnak venném a kettőt. Szimmetrikusan kezelném a területszámítást, ameddig egy adott konkrét példánál elő nem kerülne, hogy a két oldalon más-más határnál szűnik meg az 1/x-es függés. Mert ugye egy ilyet csak konkrét határok figyelembevételével lehetne kiértékelni. Ezen utosó mondatomból is következik, hogy a processzor tudja, hogy milyen értékre számol területet, vagy ha csak elkezdi a vakvilágba, akkor is tudja számolni, hogy hányadik lépésnél tart, ergo a két proci össze tudja hasonlítani, hogy melyikőjük hol tart.
Szerintem a megoldás: Vagy jelöljük mindig konkrétan, hogy mit értünk alatta vagy elfogadunk egy értelmezést alapértelmezettnek és a többit jelöljük külön. (Szerintem a szimmetrikus eléggé adja magát.)
|
| Előzmény: [1860] Lóczi Lajos, 2013-05-07 17:23:59 |
|
| [1860] Lóczi Lajos | 2013-05-07 17:23:59 |
 Az nem lenne jó, ha itt mindkettőnknek igaza lenne és a területet kétféleképpen is lehetne definiálni.
Konkrétan, melyik részlépéssel nem értesz egyet a levezetésemben? Továbbá képzeljük azt, hogy az egyik processzor a bal oldali területet számolja ki, a másik pedig a jobb oldalit: az egyik nem tud arról, hogy a másik "ugyanannyira közelíti-e a 0-t".
Mi legyen a megoldás?
|
| Előzmény: [1859] polarka, 2013-05-07 17:18:23 |
|
| [1859] polarka | 2013-05-07 17:18:23 |
 Mindkettőnknek!?
Az nyilván igaz, hogy [-1,0) között a fv -1 szerese a (0,1] közötti részének, tehát előjeles összegük 0-ra kell kijöjjön, ha ugyanannyira közelíted a 0-t mindkét oldalról. Ha pedig a feltétel nem teljesül, akkor nyilván nem lesz 0.
|
| Előzmény: [1858] Lóczi Lajos, 2013-05-07 16:53:33 |
|
|
|
| [1856] Lóczi Lajos | 2013-05-07 16:13:32 |
 Egyetértek, a cél nyilván az, hogy ezeket a formulákat pl. területszámításra használjuk. De akkor meg kell kérdezzem, hogy a korábbi c1=c2=c választással kapott primitívfüggvény-sereg megfelel-e a területszámítási intuíciónknak:
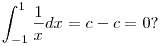
Vagyis ebben a példában a szimmetrikus területet valóban 0-nak szeretnénk definiálni?
|
| Előzmény: [1855] polarka, 2013-05-07 16:06:46 |
|
| [1855] polarka | 2013-05-07 16:06:46 |
 Talán, mert ha majdan függvény alatti területként szeretné valaki használni, akkor a következő határozott integrált kapnánk 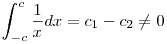 , ahol c , ahol c R+ R+
Ami nem felelne meg a területszámítási intuíciónak.
|
| Előzmény: [1854] Lóczi Lajos, 2013-05-07 15:17:27 |
|




 2)
2) 



 függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet.
függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet.  [a,b]).
[a,b]). x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon?
x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon? 

 -
-