| [1892] Róbert Gida | 2013-10-05 20:54:21 |
 Amit te írsz az egy x-re működik. Több x-nél, már lehetséges, hogy a nagyon jól közelítő nevezők teljesen mások, nincs egy nagyon jól közelítő azonos nevező.
Szimultán approximációnak nevezik a problémát, lásd http://www.shunjiito.com/paper/49109yasutomi1030.pdf (introduction első 5 sora).
ezzel (az egyébként trivi) állítással úgy nézem, hogy 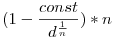 jön ki jobb oldalra az eredeti (n-1) helyett.. (itt a konstans már csak n-től függ). Amiben kell még szórakozni az eredeti bizonyításnál, hogy neked az kell, hogy jön ki jobb oldalra az eredeti (n-1) helyett.. (itt a konstans már csak n-től függ). Amiben kell még szórakozni az eredeti bizonyításnál, hogy neked az kell, hogy  i=d*xi-pi nem csak, hogy kicsi, hanem még negatív is (itt pi egész). i=d*xi-pi nem csak, hogy kicsi, hanem még negatív is (itt pi egész).
|
| Előzmény: [1890] w, 2013-10-05 14:30:26 |
|
|
| [1890] w | 2013-10-05 14:30:26 |
 Szerintem igaz lesz. Tehát az a kérdés, hogyha a1,a2,...,an>0 valós számok, létezik-e olyan d>0 valós, mellyel
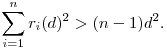
Itt ri(d) [0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d) [0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d)  i=1,2,...,n. i=1,2,...,n.
Most ezt először átrendezzük, hogy átlássuk a szerkezetét:
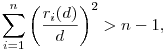
azaz nekünk jó közel kell hoznunk a 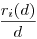 hányadosokat az 1-hez, de úgy, hogy az 1-et még ne érjük el. hányadosokat az 1-hez, de úgy, hogy az 1-et még ne érjük el.
A megoldási ötletem az volna, hogy tfh. 0<a1 a2 a2 ... ... an, és csináljunk racionális approximációt: an, és csináljunk racionális approximációt: 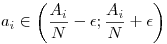 legyen legyen  i, ahol N, Ai egészek. Vegyük i, ahol N, Ai egészek. Vegyük 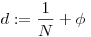 -t, ekkor ai<Aid, ai/d<Ai kellene nekünk, ahol ai/d nagyon közel van Ai-hez. De -t, ekkor ai<Aid, ai/d<Ai kellene nekünk, ahol ai/d nagyon közel van Ai-hez. De 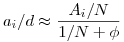 , így ez talán jó lesz, hisz , így ez talán jó lesz, hisz  , , >0 akármilyen kicsi, de egymáshoz képest akármilyen nagy. (Rendesen le kellene tisztítani határértékügyileg, ez még elvi hibás is lehet.) >0 akármilyen kicsi, de egymáshoz képest akármilyen nagy. (Rendesen le kellene tisztítani határértékügyileg, ez még elvi hibás is lehet.)
|
| Előzmény: [1888] Sinobi, 2013-10-05 13:15:24 |
|
|
| [1888] Sinobi | 2013-10-05 13:15:24 |
 Igaz-e, hogy minden nemnegatív a1, a2, ... an valós számok esetén létezik olyan d valós szám, hogy 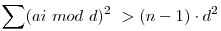 ? (a modulo pozitív értéket ad vissza). Ebből már következne egy másik állítás, amiből egy megint másik, amiből a feladat, de ez ehhez hozzá se tudok nyúlni, nem is látszik igaznak :( Van valakinek ötlete? Másik becslése, ellenpéldája, stb? ? (a modulo pozitív értéket ad vissza). Ebből már következne egy másik állítás, amiből egy megint másik, amiből a feladat, de ez ehhez hozzá se tudok nyúlni, nem is látszik igaznak :( Van valakinek ötlete? Másik becslése, ellenpéldája, stb?
|
|
| [1887] koma | 2013-10-03 22:47:30 |
 köszi mindenkinek a hozzászólását, tényleg nem volt egy "nehéz" feladat, de valahogyan nem jöttem mégsem rá... sebaj, most már okosabb lettem, köszönöm:)
|
|
| [1886] w | 2013-10-03 20:04:50 |
 Ez igazából ugyanaz a megoldás: a3-3ab=35, ab=30 után a3=(x+y)3=125, x+y=5. Köszi viszont, hogy leírtad. (Direkt azért úgy mutattam be, mert kicsit általánosabb, pl. alkalmas az x+y=3, x4+y4=17 egyenletrendszer megoldására is.)
Fálesz Mihálynak is köszönöm a megoldási ötletét/módszerét, nagyon érdekes volt.
|
| Előzmény: [1884] Alekszandrov, 2013-10-03 11:20:52 |
|
|
| [1884] Alekszandrov | 2013-10-03 11:20:52 |
 Van másik megoldás is, nem kell ehhez a és b! :-)
A második egyenletet szorozd meg hárommal, majd add össze az elsővel, így x+y köbe egyenlő 125-tel, tehát x+y=5. Majd a második egyenletet szorzattá alakítva, az x+y helyébe beírva az 5-öt, kapjuk: xy=6 Ez a két egyenlet már ránézésre is megoldható!
|
| Előzmény: [1883] koma, 2013-09-30 10:02:34 |
|
|
| [1882] w | 2013-09-29 22:42:37 |
 Szia Koma!
Az 1) feladatod klasszikus példa az ún. elemi szimmetrikus polinomok alkalmazására. Tehát az ilyen szimmetrikus kifejezéseket ki lehet fejezni a:=x+y és b:=xy segítségével: 35=x3+y3=(x+y)(x2-xy+y2)=(x+y)[(x+y)2-3xy]=(x+y)3-3xy(x+y)=a3-3ab és 30=x2y+xy2=xy(x+y)=ab. Innen már nem olyan nehéz befejezni.
2) 3) Vedd észre, hogy a2 0 és |a| 0 és |a| 0, ahol egyenlőség épp akkor áll fenn, ha a=0. 0, ahol egyenlőség épp akkor áll fenn, ha a=0.
|
| Előzmény: [1881] koma, 2013-09-29 20:13:57 |
|
| [1881] koma | 2013-09-29 20:13:57 |
 Az alábbi feladatok megoldásában kérném a segítségeteket:
1,Oldjuk meg az alábbi egyenletrendszert! x3+y3=35, b, x2y+y2x=30
ugyebár a= (x+y)(x2-xy+y2) b= xy(x+y), de hogyan tovább?
2, (x2-1)2+(x4-1)2=0 látom, hogy másodfokú egyenletre vezet, de nem látom a megoldását
3, abs (x+y-13) + abs (y-z-5) abs (y-z-2) =0
nagyon szépen köszönöm előre is a segítséget, és további szép estét kívánok!
|
|
|
|
| [1878] koma | 2013-09-28 18:59:33 |
 Sziasztok, akadt két problémám, nagyon megköszönném, ha valaki kisegítene.:)
1, Határozza meg az a1=1,an+1=2an (n term szám) rekurzív sorozat képletét.
2,Mutassuk meg, hogy az alábbi rekurzív sorozat monoton csökkenő: a1=2,a2=1,an+1=5an-6an-1,(n 2) 2)
köszönöm szépen a segítséget.
|
|
| [1877] bianka | 2013-09-28 10:25:42 |
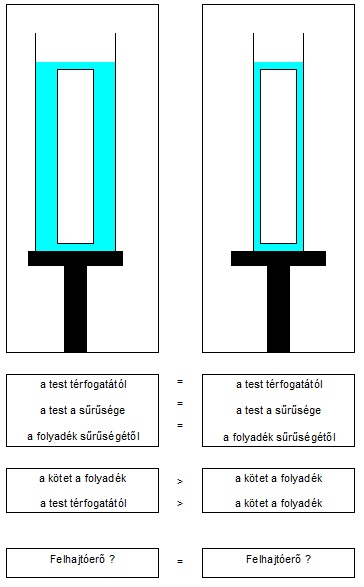
 szia!
egy gyors kérdés (skicc)
köszi! ...bianka
|
 |
|
| [1876] gyula60 | 2013-09-17 20:11:06 |
 Javaslom az 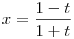 helyettesítés alkalmazását, amely után a kanonikus alakra hozás jobban megvalósítható. helyettesítés alkalmazását, amely után a kanonikus alakra hozás jobban megvalósítható.
A keresett primitív fügvényt a következő két f1(x) és f2(x) függvény összege állítja elő:
![f_1(x)=-\frac{1}{\sqrt2}arc\tg\bigg[\frac{\root\of{x^2+x+1}}{\sqrt2(x-1)}\bigg]](keplet.cgi?k=7F83EA544685A758) , ,
![f_2(x)=-\frac{1}{\sqrt6}\ln\bigg[\frac{\sqrt2(x+1)-\root\of{3(x^2+x+1)}}{\root\of{(x^2-x+1)}}\bigg]](keplet.cgi?k=B1C572E2B7464A7A) . .
|
| Előzmény: [1874] juantheron, 2013-09-02 21:12:42 |
|
|
|
| [1873] Lóczi Lajos | 2013-05-24 15:17:24 |
 Kedves Mihály,
szerintem érdemes elkülöníteni a különböző célcsoportokat.
A gyakorlatban előkerülő szakaszonként sima függvények integrálásához mindenki a Newton--Leibniz-formulát fogja akarni használni; ez a célcsoport nem akar Dirichlet-függvényt integrálni, vagy bármit az integrál definíciója alapján kiszámítani. A HK-elmélet keretében a Newton--Leibniz-tételkör nagyon természetes módon tárgyalható, ami nem mondható el a Riemann- vagy a Lebesgue-elméletről. Ez a célcsoport nem fog semmilyen  függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet. függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet.
Egy következő célcsoport lehet az, akik látják, hogy van pl. Dirichlet-függvény, és ezt konstans  -val nem lehet integrálni (azaz Riemann-értelemben), de egy kicsit bonyolultabb -val nem lehet integrálni (azaz Riemann-értelemben), de egy kicsit bonyolultabb  -val már lehet. Ha e célcsoport tagjai ezt a -val már lehet. Ha e célcsoport tagjai ezt a  függvényt bonyolultnak találják, akkor nekik a Lebesgue-elmélet sem lenne emészthető. De itt sem muszáj a "definíció" szerinti integrálást erőltetni, a Dirichlet-fv. integráljának értéke a tételekből úgyis "kijön". függvényt bonyolultnak találják, akkor nekik a Lebesgue-elmélet sem lenne emészthető. De itt sem muszáj a "definíció" szerinti integrálást erőltetni, a Dirichlet-fv. integráljának értéke a tételekből úgyis "kijön".
Aki pedig absztrakt Lebesgue-elméletet akar tanulni, annak -- a Lebesgue-elmélet megismerése előtt -- nagyon tanulságos lehet látni, hogy milyen gyorsan el lehet jutni egy [a,b]-n értelmezett függvény integráljának definíciójához, amit később majd Lebesgue-integrálnak fogunk hívni és egy bonyolultabb apparátus keretében absztraktabban és általánosabban felépíteni.
|
| Előzmény: [1872] Fálesz Mihály, 2013-05-24 10:34:11 |
|
| [1872] Fálesz Mihály | 2013-05-24 10:34:11 |
 Kedves Lajos,
A kérdésed az volt, hogy a HK integrál miért nem vette át pl. az egyetemi tananyagban a Riemann-integrál helyét.
Több okot is látok. Az egyik didaktikai. Én legalábbi személy jobban szeretem, ha a világot apránként fedezzük fel. Előbb találunk néhány mozaikdarabot, ezeket tanulmányozzuk, emésztjük, és csak utána építünk fel valami általánosabb rendszert, aminek a sok darab mind része. Számomra mindig elrettentő példát jelentenek az olyan esetek, ahol előbb kimondanak és bebizonyítanak egy nagyon absztrakt tételt, és utána ennek speciális esete lesz a többi, külön-külön sokkal érdekesebb állítás.
A másik ok, hogy nem akarunk túl sok fölösleges dolgot tanítani. Egy mérnök vagy egy alkalmazott matematikus szép, szakaszonként sima függvényekkel dolgozik, és valószínűleg soha nem akarja mondjuk a Dirichlet-függvényt integrálni. Nekik bőven elég az (improprius) Riemann-integrál, és az x2 integrálása sem okoz túl nagy traumát egyenletes felosztással. Semmi nyereség nincs mindaddig, amíg csak véges sok pont közelében van gond a függvénnyel. Az improprius integrált (végtelen inervallumokon) úgysem ússzuk meg.
Azt is írtad, hogy a definíciók közötti különbség alig észrevehető, a nyereség viszont nagy.
Az alig észrevehető különbség valójában óriási. Persze, mondhatjuk ártatlan arccal, hogy konstans  helyett inkább egy pozitív értékű függvényt veszünk, de ez félrevezető. A többség valami viszonylag szép helyett inkább egy pozitív értékű függvényt veszünk, de ez félrevezető. A többség valami viszonylag szép  függvényt fog várni, tévesen. Nehezen fogják megemészteni azt a sokkot, hogy a várt szakaszonként folytonos függvény helyett miféle szörnyűségekbe ütközhetnek; hogy egy kicsit csúnyább függvény (pl. a Dirichlet-függvény) integrálásához mennyire bonyolult függvényt fog várni, tévesen. Nehezen fogják megemészteni azt a sokkot, hogy a várt szakaszonként folytonos függvény helyett miféle szörnyűségekbe ütközhetnek; hogy egy kicsit csúnyább függvény (pl. a Dirichlet-függvény) integrálásához mennyire bonyolult  függvényt érdemes választani. függvényt érdemes választani.
Ha pedig elkezdjük vizsgálni, hogy egyes függvények miért (nem) HK integrálhatók, óhatalanul beleütközünk a Lebesgue-mérték hiányába. Ezért gondolom, hogy a HK integrállal a mértékelmélet után érdmes foglalkozni.
|
| Előzmény: [1870] Lóczi Lajos, 2013-05-23 22:23:19 |
|
| [1871] Lóczi Lajos | 2013-05-23 23:58:10 |
 Szerintem az alapvető tételek bizonyításai nem nehezebbek, lásd pl. Lee Peng-Yee: Lanzhou Lectures on Henstock Integration c. művét 1989-ből, amely a fogalom felépítésére koncentrál.
Vagy érdemes egy pillantást vetni erre a masszívabb könyvre Brian S. Thomson: Theory of the integral, amely összehasonlító szempontból tárgyal viszonylag sok integrálfogalmat.
De hogy a Riemann-integrál fogalma is rejteget még nemtriviális részleteket: 2009-ben adták meg annak szükséges és elégséges feltételét, hogy egy F függvény előálljon, mint egy f Riemann-integrálható függvény integrálfüggvénye. Azaz: mik a feltételek F-re, hogy létezzen hozzá egy c konstans és f Riemann-integrálható függvény, hogy 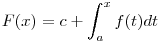 legyen (x legyen (x [a,b]). [a,b]).
|
| Előzmény: [1868] jonas, 2013-05-23 15:10:52 |
|
| [1870] Lóczi Lajos | 2013-05-23 22:23:19 |
 Ahhoz mennyi előkészületre van szükség (a definíciókkal együtt), hogy az x x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon? x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon?
Véleményem szerint ennél kevesebb vesződséggel jár a Dirichlet-függvényről megmutatni a definíciókból, hogy HK-integrálja 0.
Ha nem cél az absztrakt mértékelmélet tanulmányozása, a HK-integrál fogalma kifizetődőbben felépíthető, mint a Lebesgue-integrálé.
|
| Előzmény: [1869] Fálesz Mihály, 2013-05-23 17:09:02 |
|
| [1869] Fálesz Mihály | 2013-05-23 17:09:02 |
 Szerintem nem olyan egyszerű ez az integrálfogalom, és inkább a mértékelmélet tárgyalása után érdemes foglalkozni vele.
Például próbáljuk integrálni a Dirichlet-függvényt, vagy a Cantor halmaz összes racionális eltoltja uniójának karakterisztikus függvényét a [0,1] intervallumban.
|
| Előzmény: [1865] Lóczi Lajos, 2013-05-14 23:49:32 |
|
|



 i=d*xi-pi nem csak, hogy kicsi, hanem még negatív is (itt pi egész).
i=d*xi-pi nem csak, hogy kicsi, hanem még negatív is (itt pi egész).
 )-re szerintem ez nem igaz. (vagy nem látom, hogy
)-re szerintem ez nem igaz. (vagy nem látom, hogy 
 [0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d)
[0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d)  i=1,2,...,n.
i=1,2,...,n.  a2
a2


 0 és |a|
0 és |a|


 függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet.
függvényt várni, és nem kapnak sokkot szörnyű függvényektől: a mindennapi praktikus számításokban nem látnak ilyet.  x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon?
x2 függvény Lebesgue-integrálját ki tudjuk számítani a [0,1] intervallumon? 