| [1962] marcius8 | 2014-11-27 14:13:22 |
 Köszi a szép és nagyon egyszerű megoldást!!!!!!! Az #1961 hozzászólásban levő összefüggés szerintem is beillene egy versenyfeladatnak. Tisztelettel: Bertalan Zoltán.
|
| Előzmény: [1960] emm, 2014-11-26 21:33:49 |
|
| [1961] Ali | 2014-11-27 09:22:28 |
 Szép megoldás.
Lett egy azonosság, ami első ránézésre nem tűnik triviálisnak:
&tex;\displaystyle \sum_{k=1}^l{k\binom{l}k\sum_{\matrix{i_1+i_2+...+i_k=n\cr i_1,i_2,...i_k\ge1\cr}}^k{\frac{n!}{i_1!i_2!...i_k!}{\bigg(\frac1{l}}\bigg)^n}} = l-l\Big(\frac{l-1}{l}\Big)^n&xet;
ahol az &tex;\displaystyle i_1+i_2+...+i_k=n&xet; felbontásban a sorrend számít és &tex;\displaystyle n\ge{l}.&xet;
|
| Előzmény: [1960] emm, 2014-11-26 21:33:49 |
|
| [1960] emm | 2014-11-26 21:33:49 |
 Legyen &tex;\displaystyle n&xet; ember és &tex;\displaystyle l&xet; emelet. &tex;\displaystyle X&xet; legyen a megnyomott gombok száma, &tex;\displaystyle X=\sum_{i=1}^l A_i&xet;, ahol &tex;\displaystyle A_i=0&xet;, ha nem nyomták meg a gombot, és &tex;\displaystyle 1&xet;, ha megnyomják, valamint legyen &tex;\displaystyle B_i&xet; az az esemény, hogy valaki megnyomja az &tex;\displaystyle i&xet;-ik gombot. De ekkor &tex;\displaystyle E(A_i)=P(B_i)&xet; és &tex;\displaystyle P(B_i)=P(B_j)&xet;.
&tex;\displaystyle E(X)=E\Big(\sum_{i=1}^l A_i\Big)=\sum_{i=1}^l E(A_i)=\sum_{i=1}^l P(B_i)=lP(B_1)=l-l\Big(\frac{l-1}{l}\Big)^n&xet;
|
|
| [1959] Ali | 2014-11-26 10:29:06 |
 &tex;\displaystyle \sum_{k=1}^{20}{k\binom{20}{k}\sum_{i_1+i_2+...+i_k=30,\forall{i_j}>0}^k{\frac{30!}{i_1!i_2!...i_k!}{\bigg(\frac1{20}}\bigg)^{30}}}&xet;
Az &tex;\displaystyle i_1+i_2+...+i_k=30&xet; felbontásban a sorrend számít.
|
| Előzmény: [1954] marcius8, 2014-11-25 11:18:40 |
|
|
|
|
|
| [1954] marcius8 | 2014-11-25 11:18:40 |
 Tegyük fel, hogy a szuper-hilton szálloda földszintjén beszáll a liftbe 30 ember. A szálloda 20 emeletes, tehát a liftben a "földszint" gombon kívül 1-től 20-ig számozott gombok találhatóak. A 30 ember mindegyike megnyomja a számozott gombok valamelyikét (egy ember pontosan egy gombot nyom meg), annak megfelelően hogy ki melyik szintre akkar a lifttel megérkezni. Természetesen tekinthetjük úgy, hogy akármelyik ember akármelyik gombot egyforma (1/20) valószínűséggel nyomja meg. Mennyi lesz a megnyomott gombok számának várható értéke? Tisztelettel: Bertalan Zoltán.
|
|
| [1953] Old boy | 2014-11-23 09:22:21 |
 A B.4612 sz. feladat (2014 március) megoldását keresem (a "Lejárt..." menüpont alá is feltettem a kérést). Előre is kösz!
|
|
|
| [1951] HoA | 2014-11-20 16:35:26 |
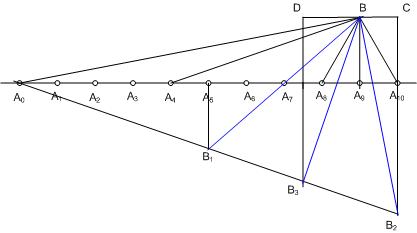
 Talán ilyesmire gondoltál: Kövessük a közölt megoldás gondolatmenetét és mutassuk meg, hogy 2-2 szög 30 fokra egészíti ki egymást. Tükrözzük az &tex;\displaystyle A_4 A_9 B \Delta&xet; -et az &tex;\displaystyle A_0 A_{10}&xet; egyenesre és toljuk el &tex;\displaystyle A_4 et A_0 ba&xet; . B új helyzete legyen &tex;\displaystyle B_1&xet; . Ekkor &tex;\displaystyle B A_0 B_1 \angle&xet; -ről kell megmutatni, hogy &tex;\displaystyle 30^\circ&xet; -os.
Vegyük fel az &tex;\displaystyle A_0 B_1&xet; egyenesen &tex;\displaystyle B_2&xet; -t úgy, hogy &tex;\displaystyle A_0 B_1 = B_1 B_2&xet; legyen . Ekkor &tex;\displaystyle B_1 A_5 = \sqrt 3 , B_2 A_{10} = 2 \sqrt 3&xet; . A &tex;\displaystyle B_2 A_{10}&xet; egyenesen legyen C az a pont, melyre &tex;\displaystyle B B_2 C \Delta&xet; derékszögű. &tex;\displaystyle B C / C B_2 = 1 / (3 \sqrt 3) = \sqrt 3 / 9&xet; . &tex;\displaystyle A_0 A_9 B \Delta&xet; -ben &tex;\displaystyle B A_9 / A_0 A_9 = \sqrt 3 / 9&xet; . A két háromszög hasonló, &tex;\displaystyle A_0 B B_2 \angle = 90^\circ&xet; , ezért &tex;\displaystyle B_1 A_0 = B_1 B_2 = B_1 B&xet;. Legyen &tex;\displaystyle B_1 B_2&xet; felezőpntja &tex;\displaystyle B_3&xet; . A &tex;\displaystyle B_3&xet; -ból &tex;\displaystyle A_0 A_{10}&xet; egyenesre bocsátott merőlegesen D az a pont, melyre &tex;\displaystyle B_3 B D \Delta&xet; derékszögű. &tex;\displaystyle BD / D B_3 = (3/2)/(5/2)\sqrt 3 = \sqrt 3 / 5&xet; . &tex;\displaystyle B_1 A_5 / A_5 A_0 = \sqrt 3 / 5&xet; . &tex;\displaystyle B B_3&xet; merőleges &tex;\displaystyle A_0 B_1&xet; -re, &tex;\displaystyle B B_1 = B B_2&xet; , a &tex;\displaystyle B B_1 B_2 \Delta &xet; szabályos, &tex;\displaystyle A_0 B_2 B \angle = 60^\circ&xet; , &tex;\displaystyle B A_0 B_1 \angle = 30^\circ&xet; .
Folytatás: készítsünk hasonló ábrát a másik szögpárra.
|
 |
| Előzmény: [1949] Kovács 972 Márton, 2014-11-19 22:12:50 |
|
|
| [1949] Kovács 972 Márton | 2014-11-19 22:12:50 |
 Sziasztok!
A 2012 szeptemberi szám B.4465-ös feladatának megoldása megtalálható itt.
Tudna valaki mutatni egy másik megoldást, amely csak és kizárólag átdarabolást használ?
Olyan megoldást találtam már, amiben ha egymás mellé mérek bizonyos szakaszokat, akkor Pitagorasz tétellel kijön az állítás, de az a sejtésem, hogy van Pit. tétel nélküli "átdarabolós" megoldás is.
Köszönöm előre is a segítséget!
|
|
| [1948] w | 2014-11-19 20:32:49 |
 Az &tex;\displaystyle x^2+y^2&xet; kétváltozós polinom konstans szorzótól eltekintve egyértelműen bontható komplex együtthatós polinomok szorzatára (B4579-hez hasonlóan belátható): &tex;\displaystyle x^2+y^2=(x+iy)(x-iy)&xet;, ahol &tex;\displaystyle i^2=1&xet; a képzetes egység. Ily módon valós együtthatós polinomok szorzatára nem is bírjuk bontani.
|
| Előzmény: [1946] mosapeter, 2014-11-19 20:07:24 |
|
| [1947] w | 2014-11-19 20:27:07 |
 Legyenek a racionális számok: &tex;\displaystyle q_1,q_2,\dots&xet;. (Ismert, hogy ezek megsorszámozhatóak.) Majd pedig legyen
&tex;\displaystyle f(x)=\sum_{q_n\le x}\frac1{2^n}.&xet;
Az &tex;\displaystyle f&xet; függvény minden valós &tex;\displaystyle x&xet;-re is értelmezett, monoton növekvő, de egyik racionális helyen sem lesz folytonos.
|
| Előzmény: [1945] zsivel, 2014-11-19 19:44:55 |
|
| [1946] mosapeter | 2014-11-19 20:07:24 |
 Sziasztok!
Érdeklődni szeretnék ,hogy az a2 + b2 faktorizálható-e?
|
|
| [1945] zsivel | 2014-11-19 19:44:55 |
 Sziasztok!
Amit keresek (már napok óta):
Példát olyan f: [a,b]->R függvényre, mely szakaszonként monoton, de nem szakaszonként folytonos. Minden segítséget előre is köszönök!
|
|
| [1944] Petermann | 2014-11-11 17:10:12 |
 Sziasztok, ezt a feladatot hogyan kéne megoldanom? Nagyon köszönök minden segítséget.:)
|
 |
|
|
|
| [1941] machobymb | 2014-10-15 22:38:18 |
 Helyezz el zárójeleket úgy a műveletsorban, hogy teljesüljön az egyenlőség:
48 : 6 + 2 * 8 - 6 : 3 = 60
Már egy napja töröm rajta a fejem. Szerintem elírták. Várom a megoldást! Előre is köszönöm!
|
|
| [1940] Róbert Gida | 2014-09-04 21:35:43 |
 Egyszerűbben: ha &tex;\displaystyle n>1&xet; kétszeresen összetett szám, akkor &tex;\displaystyle \varphi(n)-2\le 2*\pi (n)&xet; (,mert &tex;\displaystyle \varphi(n)-2&xet; darab &tex;\displaystyle i&xet; van amelyre &tex;\displaystyle 1<i<n-1&xet; és &tex;\displaystyle n&xet;-hez relatív prím, minden ilyen &tex;\displaystyle (i,n-i)&xet; párból az egyik prím, és minden prímet legfeljebb 2-szer számoltunk). De &tex;\displaystyle \varphi(n)>c*\frac {n}{log(log(n))}&xet; (lásd wiki cikket), ebből &tex;\displaystyle \pi (n)>d*\frac {n}{log(log(n))}&xet; ami prímszámtételnek mond ellen, ha &tex;\displaystyle n&xet; nagy. Így véges sok kétszeresen összetett szám van.
|
| Előzmény: [1939] w, 2014-09-04 19:55:48 |
|
| [1939] w | 2014-09-04 19:55:48 |
 Ez akkor annak bizonyítása, hogy véges sok "kerek szám" van.
Sirpi feladata, ha jól értem, az volt, hogy igazoljuk, hogy csak véges sok &tex;\displaystyle N&xet;-hez nincs olyan hozzá relatív prím, összetett &tex;\displaystyle 0<a,b<N&xet; pár, hogy &tex;\displaystyle N=a+b&xet;. Ez annyit takar, hogy bármely &tex;\displaystyle (a,N)=1&xet; esetén, melyre &tex;\displaystyle 0<a\le \frac N2&xet;, teljesül, hogy &tex;\displaystyle a&xet; vagy &tex;\displaystyle N-a&xet; prímszám.
Most első nekifutásra úgy tűnik, hogy a feladat enged nagyságrendi számolásoknak.
Jelölje minden &tex;\displaystyle n\ge 2&xet;-re &tex;\displaystyle P(n)&xet; az &tex;\displaystyle n&xet;-nél nem nagyobb prímek szorzatát, és &tex;\displaystyle R(n)&xet; pedig az &tex;\displaystyle \frac n2&xet;-nél nem nagyobb, &tex;\displaystyle n&xet;-hez relatív prím számok szorzatát. Ha &tex;\displaystyle N&xet; teljesíti a feltételt, akkor &tex;\displaystyle P(N)\ge R(N)&xet;.
Erdős még belátta, hogy &tex;\displaystyle P(n)<4^n&xet; (indukcióval, felhasználva, hogy minden &tex;\displaystyle (n;2n]&xet;-beli prím osztja &tex;\displaystyle \binom{2n}n&xet;-et). A megoldáshoz annyit kell belátnunk, hogy &tex;\displaystyle R(N)&xet; gyorsabban nő, mint &tex;\displaystyle 4^N&xet;, ami igaznak tűnik, bár ellenőrzésre szorul.
|
| Előzmény: [1937] csábos, 2014-09-04 19:06:31 |
|
|










