|
| [2038] Kemény Legény | 2015-09-23 12:17:44 |
 "- Van-e olyan négytagú (esetleg többtagú) számtani sorozat, amelynek minden tagja négyzetszám?"
Erre úgy tűnik, szintén tagadó a válasz: pl. Győri, Hajdu és Pintér cikke (Perfect powers from products of consecutive terms in arithmetic progression, Compositio Mathematica, 2009) alapján egy még erősebb állítás is igaz:
"We prove that for any positive integers x,d and k with gcd (x,d)=1 and 3<k<35, the product x(x+d)...(x+(k-1)d) cannot be a perfect power".
A cikk alapján úgy tűnik, az &tex;\displaystyle x(x+d)...(x+(k-1)d)=by^n, (x,d)=1&xet; egyenlet megoldását már Euler is vizsgálta a &tex;\displaystyle b=1, k=4, n=2&xet; esetre. Sőt Erdős sejtése az, hogy &tex;\displaystyle k>3&xet; esetén sosem lehet egy (rel. prímekből álló) számtani sorozat &tex;\displaystyle k&xet; egymást követő elemének szorzata teljes hatvány.
|
| Előzmény: [2035] marcius8, 2015-09-23 11:39:32 |
|
|
| [2036] Kemény Legény | 2015-09-23 11:55:46 |
 "- Van-e olyan háromtagú (esetleg többtagú) számtani sorozat, amelynek minden tagja köbszám (esetleg negyedik hatvány, esetleg ötödik hatvány, ..... stb.)"
Egy gyors keresés után ezt az arxiv-os Ribet-cikket találtam.
A Conjecture 1 alapján pedig úgy tűnik, az az általános sejtés (Dénes, 1952), hogy számtani sorozatot csak triviális módon alkothatnak páratlan prímkitevő esetén.
Ebben a Theorem 3 azt állítja, hogy &tex;\displaystyle a^p+2^{\alpha}b^p+c^p=0&xet;-nak nincs megoldása az egész számok körében, ha &tex;\displaystyle 2\le \alpha\le p&xet;. Továbbá &tex;\displaystyle a^p+2b^p+c^p=0&xet;-nek nincs olyan relatív prím egész megoldása, ahol abc páros lenne. Illetve a Theorem 4 p=4k+1 alakú kitevőre igazolja a sejtést.
|
| Előzmény: [2035] marcius8, 2015-09-23 11:39:32 |
|
| [2035] marcius8 | 2015-09-23 11:39:32 |
 Sok olyan háromtagú számtani sorozat van, amelynek tagjai négyzetszámok. (Ilyen például 1, 25, 49 vagy 49, 169, 289 vagy 49, 289, 529 vagy 961, 1681, 2401 stb....) Az ilyen háromtagú sorozatok tagjainak előállítása visszavezethető pitagoraszi számhármasokra, és az ilyen sorozatok tagjaiból pitagoraszi számhármasok állíthatóak elő.
De:
- Van-e olyan négytagú (esetleg többtagú) számtani sorozat, amelynek minden tagja négyzetszám?
- Van-e olyan háromtagú (esetleg többtagú) számtani sorozat, amelynek minden tagja köbszám (esetleg negyedik hatvány, esetleg ötödik hatvány, ..... stb.)
Tisztelettel: Bertalan Zoltán.
|
|
| [2034] marcius8 | 2015-09-07 11:19:09 |
 Legyen "D(n)" az "n" elemű permutációk közül azoknak a száma, amelyeknek nincs fixpontja. Bizonyítsuk be kombinatorikus módon a következő összefüggést:
D(k)=(k-1)*(D(k-1)+D(k-2))
|
|
| [2033] marcius8 | 2015-07-09 00:32:10 |
 Tud valaki egy 8x8-as latin-görög négyzetet? És tud valaki egy 8x8x8-as görög-latin-cirill kockát? Ha igen, kérem, hogy írja le. Előre is köszönöm. BERTALAN ZOLTÁN.
|
|
|
| [2031] Bátki Zsolt | 2015-05-11 05:49:38 |
 Ez volt idén (2015) középszintű matematika feladat, 2 pontért.
3. „Minden szekrény barna.” Válassza ki az alábbiak közül annak a mondatnak a betűjelét, amelyik tagadása a fenti kijelentésnek! A) Van olyan szekrény, amelyik nem barna. B) Nincs barna szekrény. C) Van olyan szekrény, amelyik barna. D) Pontosan egy szekrény barna.
Megkérdeztem a munkahelyemen 10 embert.(mérnököket) 6 a 'B'-re tippelt. Kettő azt mondta az 'A' és a 'B' is jó. Ketten a jó 'A' megoldást.
Kérdésem, vajon az érettségin, hány százalék adott erre jó választ? Valahol ez a statisztika fellelhető a Neten?
|
|
| [2030] jonas | 2015-04-09 09:13:25 |
 A válasz az, hogy nem igaz, én néztem be valamit. Egy ellenpélda a &tex;\displaystyle \left(\matrix{1&1&0\cr 0&0&1\cr 0&1&0}\right)&xet; mátrix.
|
| Előzmény: [2029] jonas, 2015-04-09 08:48:28 |
|
| [2029] jonas | 2015-04-09 08:48:28 |
 Egy négyzetes mátrixot Hankel mátrixnak hívunk, ha bármely antidiagonálisában csak azonos elemek vannak. Például
&tex;\displaystyle T = \left(\matrix{
0&6&2&1&9\cr
6&2&1&9&8\cr
2&1&9&8&1\cr
1&9&8&1&2\cr
9&8&1&2&1\cr
}\right) &xet;
egy Hankel-mátrix.
Minket most olyan Hankel-mátrixok érdekelnek, amiknek minden eleme 0 vagy 1. Igaz-e, hogy ha egy négyzetes nulla-egy mátrix a sorainak és oszlopainak valamely permutációjával Hankel-mátrixszá alakítható, akkor csak a sorainak a permutációjával is Hankel-mátrixszá alakítható?
A kérdés onnan jön, hogy felix azt kérdezi a MathOverflow-n, hogy hány ilyen permutált mátrix van.
|
|
| [2028] marcius8 | 2015-04-05 10:45:25 |
 Kiegészítés az előző kérdésemhez: Feltehető, hogy annak a valószínősége, hogy annak a valószínűsége, hogy a 4-es metró hibamentesen "t" működik, "lambda" paraméterű exponenciális eloszlást követ. Tisztelettel: Bertalan Zoltán.
|
|
| [2027] marcius8 | 2015-04-05 10:32:41 |
 Ma reggel néztem a TV-t, és ott mondták, hogy a 4-es metró vezető nélküli próbaüzemét tervezik. Tegyük fel, hogy a 4-es metró átlagosan 60 napig tud egyfolytában hiba nélkül metróvezető nélkül működni. Ezt ellenőrizendő, a következő tesztet találták ki: A 4-es metrót egyfolytában 360 napig járatják, és mérik, hogy mennyi ideig működik vezető nélkül hibamentesen. Ha a 360 nap próbaidő alatt van meghibásodás, az időmérést 0-ról kezdve újra kezdik. Ha ezután is van meghibásodás, akkor az időmérést megint 0-ról kezdve újra kezdik. Természetesen a 360 nap alatt akárhány meghibásodás történhet akármikor, de minden egyes meghibásodás után az időmérést 0-ról kezdve újra kezdik. A teszt akkor eredményes, ha van legalább 120 nap eltelt idő, amikor a 4-es metró hibamentesen működik vezető nélkül. Mennyi annak a valószínűsége, hogy a teszt eredményes? Tisztelettel: Bertalan Zoltán.
|
|
|
| [2025] marcius8 | 2015-03-31 07:58:12 |
 Mennyi annak a valószínűsége, hogy "n" elemet véletlenszerűen sorbarendezve, a kapott elemek vagy úgy követik egymást, hogy nagyobb-kisebb-nagyobb-kisebb-.... vagy pedig úgy, hogy kisebb-nagyobb-kisebb-nagyobb-....? Bertalan Zoltán.
|
|
| [2024] Hajba Károly | 2015-03-07 20:39:24 |
 Erre a problémára már kigondoltam egy eljárást.
Mindkét fajta pontot (telekhatárpont és felirathely pont) külön-külön X és Y koordináták alapján sorba rendezem. A vizsgált terület legkisebb és legnagyobb X ill. Y koordinátája közé kell esnie a keresendő feliratpont mindkét koordinátájának. Egy nem túl bonyolult, de hosszabb telekforma ill. 'átlós' tájolás esetén max 10 vizsgálandó pont adódna, de a 20 feletti szám már nagyon extrém helyzet lenne.
|
| Előzmény: [2021] Róbert Gida, 2015-03-07 19:42:21 |
|
| [2023] Hajba Károly | 2015-03-07 20:11:40 |
 Településenként van bontva, Budapesten kerületenként. Továbbá belterület-külterület-zártkert. Ezek az egybetartozó egységek, melyekre igaz, hogy minden csomópontba (nem telekhatár-töréspont) legalább három él fut be, de ez a gyakorlatban általában nem több négynél.
Tesztelés céljából kivágható egy bármely méretű téglalap formájú terület is, de ekkor lesznek kettévágott területek. (Tervezési alaptérképként ilyeneket kapunk dwg-ben, de ez az építési engedélyes terv helyszínrajzához kell.)
|
| Előzmény: [2021] Róbert Gida, 2015-03-07 19:42:21 |
|
|
| [2021] Róbert Gida | 2015-03-07 19:42:21 |
 Heurisztika is müködik itt: legyen S a sokszög súlypontja, míg d az S és a csúcsok közötti maximális távolság. Így, ha egy p pont d-nél távolabb van S-től, akkor nem lehet a sokszögben. (és ez konkáv sokszögre is igaz természetesen).
Általában egy megyében van egy terület, így csak azokat a sokszögeket kell végignézni amik az adott megyében vannak. Egy szebb algoritmus lehetne quadtree-k alkalmazása: http://en.wikipedia.org/wiki/Quadtree .
|
|
| [2020] Erben Péter | 2015-03-07 19:41:52 |
 Szép feladat.
A valódi projektekben az adatok pontatlansága, illogikus tárolása sokszor több gondot okoz, mit az, hogy van-e jó algoritmus az elméleti problémára. A hibák javítása és az adatok "tisztítása" nehezebb, mit az eredeti kérdés megoldása.
|
| Előzmény: [2017] Hajba Károly, 2015-03-07 17:22:54 |
|
| [2019] Hajba Károly | 2015-03-07 18:31:21 |
 Itt egy minta. 14. és 16. oldal
14. oldal: A határvonal a szakasz (s ezért írtam először vonalat), a határ a lánc, s a felület a terület.
16. oldal: A tényleges állományokban csak a T_PONT, T_HATARVONAL és ezektől független T_OBJ_ATTRDB van meghatározva, azaz a [* sárga szám *] helyett [**] szerepel, így nincs a T_FELULET-hez kötve. A * az adatok közötti szakaszoló jel.
|
| Előzmény: [2015] Erben Péter, 2015-03-07 15:10:03 |
|
| [2018] Hajba Károly | 2015-03-07 17:46:47 |
 Tesztadat a szabványos DAT formátumban ill. a jelzett digitális szinten a földhivataloknál rendelkezésre állnak. Annyi észrevétellel, hogy egyes egyébként illeszkedő szakaszok elvileg közös pontja néha, ha csak kis mértékben is, de csak közel egymás mellett van. Gyanítom, hogy ez a régi rajzos térképek kézi digitalizálásának következménye. A CAD programom dwg-t fogad, s ha egy zárt görbébe kattintok, akkor azt kitölti. Sokszor ez nem sikerül és 'nem zárt görbe' hibajelzést ad, pedig ránézésre a rajzon a görbe zárt.
Majd megkérdezem, hogy (a DAT és DWG-n kívül) még milyen formátumban igényelhető adat.
|
| Előzmény: [2015] Erben Péter, 2015-03-07 15:10:03 |
|
| [2017] Hajba Károly | 2015-03-07 17:22:54 |
 Köszönöm a részletes leírást.
Tegnap este rábukkantam az (A) példádra a wikin.
A feladat teljesen az életből való, sajnos minden téren. A szakaszok a földhivatali nyilvántartásban a telekhatárokat képező ömlesztve digitalizált szakaszok, az önálló pontok ezen telkek helyrajzi szám feliratának a helye. A '90-es évek végén nagyon jól kidolgozott szabvány lett megalkotva erre, de a megvalósítás során csak a lehető legkisebb átalakítást hajtották végre. A szabványban le van írva a telek fogalma is, de a nyilvántartásban nincsenek hozzárendelve a szakaszok ill. a láncok. Pedig amennyiben ez meg lenne oldva, akkor az erre alapuló területi tervezésnél nem egy CAD-es fedvényrajzot kellene készíteni kézzel és egérrel, ami vagy illeszkedik a töréspontokhoz vagy csak megközelíti, hanem a helyrajzi számmal. A hrsz-hez csak hozzárendelem a területfelhasználási adatokat, és a többit egy program elintézi ill. precízen felrajzolja, valóságos területi kimutatást készít. De jelenleg ez csak közelítő és emiatt nem lehet hiteles.
Most indult egy pilot program a "digitális Magyarországért", s ez épp abban a városban van, ahol dolgozom és épp ismerem az egyik kulcsembert. Így teszek egy kísérletet arra, hogy ez az átalakítás is bekerülhessen idővel a programba. Ehhez látnom kell a feladat folyamatát, méretét, buktatóit, s minden közbe jöhető dolgot mivel idő és pénzügyi igényt kell adni ahhoz, hogy esetleg bekerülhessen.
|
 |
| Előzmény: [2015] Erben Péter, 2015-03-07 15:10:03 |
|
|
| [2015] Erben Péter | 2015-03-07 15:10:03 |
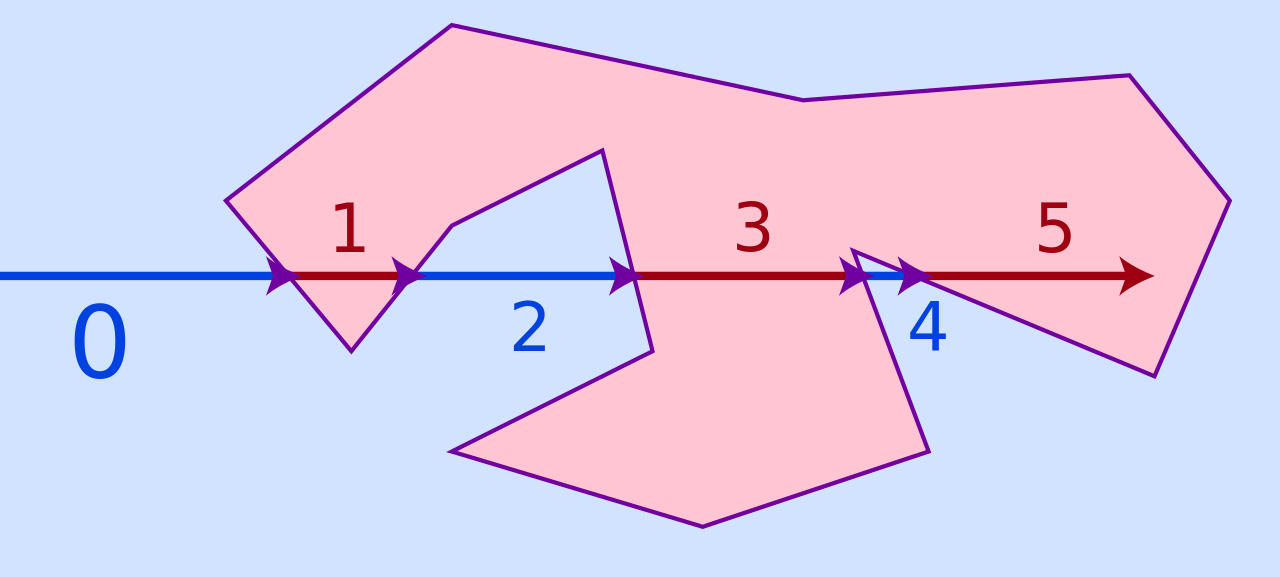
 A legtöbb helyen két módszert említenek. (A) "metszések száma" /crossing number/; (B) "kanyargási szám" /winding number/. Inclusion of a point in a polygon
Az (A) azt csinálja, hogy húz egy egyenest a ponton át, és megnézi ennek az egyenesnek és a tartományt határoló szakaszoknak az összes metszéspontját. Ezeket a metszéspontokat rendezi, és azt feltételezi, hogy ha nem történt valami baj, akkor a metszéspontok felváltva jelzik, hogy beléptünk a tartományba, majd kiléptünk belőle. Tehát ez a konkáv tartományokra is működik. Ha a pontunk előtt páratlan sok metszéspont van az egyenesen (valamelyik irányból), akkor bent vagyunk, ha páros, akkor kint.
A gyakorlati megvalósításkor sok-sok nehézséggel szembesülünk.
1. Ha az egyenes átmegy a tartomány egy csúcsán, akkor azt két metszéspontnak hihetjük (a két szomszédos szakaszon egy-egy.)
2. Ha az egyenesre esik valamelyik határ szakasz, akkor ott végtelen sok közös pont van, és nem léptünk se be se ki.
3. Nem mindegy, hogy valós vagy egész aritmetikát alkalmazunk, mert egy egyenes és egy szakasz, illetve a pont és valamelyik szakasz nagyon közel eshet egymáshoz. Valós aritmetikát használva baj lehet a kerekítési hibákból, egész aritmetikánál pedig hatalmasra nőhetnek a nevezők és a számlálók, azért nem elegendők a programozási nyelvek beépített típusai. Ha az egész probléma eredete grafikai, és csak a képernyőn akarjuk pontokról eldönteni, hogy egy képernyőre rajzolt pixel egy képernyőre rajzolt tartományhoz képest hol van, akkor kevésbé kell félni a numerikus dolgoktól, mert a pixel méreténél kisebb hibák úgysem fognak látszani.
A (B) azon alapul, hogy megszámolja, hányszor kerüli meg a poligon a pontot. Akkor van kívül egy pont, ha nullaszor. Valahogy úgy megy a számolás, hogy a körüljárás szerint sorra vesszük a tartományt határoló szakaszokat, és mindegyikre kiszámoljuk, mekkora szögben látszik (irányított szakasz, irányított szög) a pontból. Külső pontra az előjeles szögek összege nulla, ez szemléletesen látszik konvex tartomány esetén.
Itt meg az a gond, hogy rengeteg inverz trigonometrikus függvényhívást csinálunk, ami lassú és ott is lehetnek kerekítési problémák.
Ha vannak konkrét bemenő adataid (amik nem titkosak), az érdekelne, mert ehhez a problémához nem egyszerű jó tesztadatokat gyártani.
|
| Előzmény: [2013] Hajba Károly, 2015-03-06 16:56:29 |
|









