|
|
| [2059] Róbert Gida | 2015-12-14 23:42:42 |
 &tex;\displaystyle K>0&xet; alsó korláttal meg már igaz: legyen m>0 olyan egész, hogy &tex;\displaystyle \frac 1m<K&xet;, ekkor mivel minden intervallum legalább &tex;\displaystyle K&xet; hosszú, ezért tartalmaz legalább egy darab &tex;\displaystyle \frac lm&xet; alakú pontot. Így skatulyaelv miatt a végtelen sok intervallum valamelyik ilyen pontot végtelen sokszor tartalmazza. "Hasonló" gondolatmenet megy magasabb dimenzióban.
|
| Előzmény: [2058] Sinobi, 2015-12-14 22:11:22 |
|
| [2058] Sinobi | 2015-12-14 22:11:22 |
 És ha az intervallumok méretének adunk valami K alsó korlátot? (azt sejtem, hogy így már nem lehet)
És ha nagyobb (mondjuk 2) dimenzióban akarunk ilyen, >K méretű kockákkal fedni?
Vagy, ha még azt is megengedjük, hogy olyan alakzatokkal fedünk, amelyek előállnak véges sok téglatest uniójaként/metszeteként?
(ezeket próbáltam, sikertelenül. Állítólag valamelyik Lebesgue integrálos tétellel könnyű, de én azt nem tudom. Sőt, még az eredményt sem igazán.)
|
| Előzmény: [2056] Róbert Gida, 2015-12-14 17:34:37 |
|
|
|
| [2055] Sinobi | 2015-12-13 21:30:23 |
 Igaz-e hogy ha az egység intervallumba elhelyezünk végtelen sok zárt intervallumot, hogy az összhosszuk divergens, akkor biztosan létezni fog legalább 1 pont, amelyik végtelen sok által van lefedve? (R felett)
|
|
|
|
|
| [2051] emm | 2015-12-06 16:43:16 |
 &tex;\displaystyle D:=(A\cup B\cup C)^c&xet;, ekkor &tex;\displaystyle {P}(D)=1-p-q-r&xet;. Ekkor lényegében egy 4 oldalú cinkelt "kockával" dobunk. Legyen a keresett valószínűség &tex;\displaystyle R_n&xet;. Feltételezzünk arra, hogy az első dobás, amikor &tex;\displaystyle D&xet;-től különbözőt dobunk, &tex;\displaystyle k&xet;, legyen ez az esemény &tex;\displaystyle S_k&xet;, és a &tex;\displaystyle k&xet;-ik dobás &tex;\displaystyle X_k&xet;, a függetlenséget használva adódik, hogy:
&tex;\displaystyle
P(S_k)=P\left(X_{k}\neq D\cap\bigcap_{j=1}^{k-1}X_j=D \right)=P(X_k\neq D)\prod_{j=1}^{k-1}P(X_j=D)=(1-p-q-r)^{k-1}(p+q+r)
&xet;
Ebből a nekünk megfelelő eset az, amikor &tex;\displaystyle A&xet;-t dobunk, így az &tex;\displaystyle A&xet;, &tex;\displaystyle B&xet;, &tex;\displaystyle C&xet; események páronként kizáró volta miatt: miatt:
&tex;\displaystyle
P(S_k\cap X_k=A)=P\left(X_{k}=A\cap\bigcap_{j=1}^{k-1}X_j=D \right)=P(X_k=A)\prod_{j=1}^{k-1}P(X_j=D)(1-p-q-r)^{k-1}p
&xet;
Vagyis &tex;\displaystyle n&xet; dobás esetén, alkalmazva a mértani sor összegképletét:
&tex;\displaystyle
P(R_n)=\sum_{i=1}^nP(S_i\cap X_i=A)=p\sum_{i=0}^{n-1}(1-p-q-r)^{i}
=p\frac{1-(1-p-q-r)^n}{p+q+r}
&xet;
Ha &tex;\displaystyle p,q,r>0&xet;, akkor &tex;\displaystyle n\to\infty&xet; esetén a keresett valószínűség tart &tex;\displaystyle \frac{p}{p+q+r}&xet;-hez. (és nem okoz problémát, ha &tex;\displaystyle p+q+r=1&xet;).
|
| Előzmény: [2049] lorantfy, 2015-12-05 19:56:56 |
|
|
| [2049] lorantfy | 2015-12-05 19:56:56 |
 Az A, B és C egymást kizáró események P(A)=p, P(B)=q, P(C)=r. Mennyi a valószínűsége n független kísérletet elvégezve, hogy A előbb következik be mint B vagy C? Mi lesz e valószínűség határértéke, ha n tart a végtelenbe?
|
|
| [2048] lorantfy | 2015-12-05 19:46:07 |
 Adott egy gömbön az AB ív. Hol vannak a gömbfelületen azok a C pontok, melyekre az ABC gömbháromszög területe egy adott állandó.
|
|
| [2047] Jhony | 2015-12-05 19:23:55 |
 - köszönöm szépen a válaszokat ! - a továbbiakban folytatnám a gondolatot,tekintsük nulladik lépésnek az előzőekben felírt és elfogadott,bizonyítást nem igénylő képletet,azaz
0. &tex;\displaystyle 2^a *(2b+1)=N&xet; képletet, ,,a" és ,,b" eleme az N+(0) -nak 1. tudjuk,ha &tex;\displaystyle 2^a&xet; azaz 2-őt az ,,a" hatványon ,,a"-szor osztjuk 2-vel az eredmény 1 2. ha (2b+1) -et beszorozzuk 3-mal és hozzáadunk 1-et ,azaz (2b+1)*3 +1 = 6b+4 azaz 6b+4 = 2(3b+2) vagyis az eredmény ismét egy páros szám amit osztva 2 -vel kapjuk a (3b+2),ami páratlan 3. ha a (3b+2) -őt beszorozzuk 3-mal és hozzáadunk 1-et ,azaz (3b+2)*3 +1 = 9b+7 4. bizonyítsuk be,hogy &tex;\displaystyle (9b+7)=2^x&xet; ahol ,,x" természetes szám,vagyis bizonyítsuk be,hogy a fent említett képletből bármely (2b+1) számra folytatván a sort,azaz szorozva 3-mal plusz 1 ,osztva 2 -vel majd ismét szorozva 3-mal plusz 1 előbb-utóbb 2 hatványát eredményezi .
|
|
| [2046] nadorp | 2015-12-05 13:47:32 |
 Úgy kaphatsz ilyet:
&tex;\displaystyle 2^a(2b+1)&xet;
ha 2^a(2b+1) elejére és végére egy $ jelet írsz. A matematikai mód ezzel a jellel kezdődik és végződik.
|
| Előzmény: [2044] Jhony, 2015-12-05 01:43:56 |
|
| [2045] csábos | 2015-12-05 09:12:48 |
 Kedves Jhony!
Amit írsz, az a számelmélet alaptételéből következik:
Minden nem 0 és nem 1 nem -1 egész szám felírható prímszámok (prímhatványok) szorzatatként és ez az előállítás előjeltől és sorrendtől eltekintve egyértelmű.
pl &tex;\displaystyle 1800=2\cdot 3\cdot 3\cdot 5\cdot2\cdot2\cdot 5&xet;, vagy &tex;\displaystyle 1800=-3\cdot 2\cdot (-2)\cdot 5\cdot2\cdot3\cdot 5&xet;
Kanonikus alaknak hívjuk azt, amikor a prímtényezőket csoportosítjuk, és a megfelelő kitevőn írva szorozzuk őket össze, pl &tex;\displaystyle 1800=2^3\cdot 3^2\cdot 5^2&xet;
Esetünkben: ha &tex;\displaystyle n&xet; páratlan, akkor &tex;\displaystyle n=2b+1&xet; valamilyen &tex;\displaystyle b&xet; egész számra és
&tex;\displaystyle n=2^0(2b+1)&xet;
Ha &tex;\displaystyle n&xet; osztható kettővel, akkor &tex;\displaystyle n&xet; prímtényezős felírásában szerepel a kettő. Írjuk föl &tex;\displaystyle n&xet; kanonikus alakját: &tex;\displaystyle n=2^\alpha\cdot p_1^{\beta_1}\cdots p_t^{\beta_t}&xet; Most a kettőhatvány utáni rész páratlan, azaz &tex;\displaystyle 2b+1&xet; alakú, így &tex;\displaystyle n=2^\alpha(2b+1)&xet;.
Hátra van még az 1, mert arról nem szól a számelmélet alaptétele: &tex;\displaystyle 1=2^0(2\cdot 0+1)&xet;
|
| Előzmény: [2044] Jhony, 2015-12-05 01:43:56 |
|
| [2044] Jhony | 2015-12-05 01:43:56 |
 Tisztelt fórumozók ! - kérdésem ki hogyan bizonyítaná be,hogy az alábbi képlet alkalmas minden N természetes szám felírására :
(2)'a *(2b +1) = N vagyis 2 az ,,a" hatványon szorozva (2b+1) = N bocsánat,de kitéve a hatványkitevőt a következő üzenetet kaptam :,,Hiba: A ,,hatványkitevő" parancs csak matematikai módban használható " - tudván,hogy a és b eleme az N + (0) vagyis a és b eleme a természetes számok halmazának plusz nulla
- elképzelésem a ,,reductio ad absurdum" vagyis visszavezetés a lehetetlenre
(2)'0 *(2*0 +1) =/= 1 vagyis azaz 2 a nulla hatványon szorozva ... 1 *(0 +1) =/= 1 vagyis
1 =/= 1 ami tudjuk,hogy nem igaz,
- vélemények ?
- segítségeteket nagyon szépen köszönöm !
|
|
| [2043] lorantfy | 2015-11-27 13:50:35 |
 Megoldást szeretnél vagy csak segítséget? Feltehetjük, hogy minden matematikus egyformán, okosan gondolkodik. Ahogy biztosan megtudja, hogy maszatos lett leszáll és megmossa az arcát. Kezd el 2 emberrel és gondold végig a lehetőségeket, aztán ha kell növeld a számukat!
|
| Előzmény: [2042] marcius8, 2015-11-23 08:16:55 |
|
| [2042] marcius8 | 2015-11-23 08:16:55 |
 Matematikusok egy vonaton születésnapi bulit rendeznek, és egy csokistortát majszolgatva összemaszatolják magukat. A kalauz jegyellenőrzés közben megjegyzi, hogy némelyik matematikusnak csokikrémes lett a füle. A matematikusok persze rögtön elszégyellik magukat, és ezután egy szót sem szólnak egymáshoz. Persze látják egymást, de magukat nem, ugyanis a vonaton nincsen tükör. A matematikusok a vonaton még megmosakodni sem tudnak, mert a vonaton nincs víz. A kalauz persze jó tanácsként közli a matematikusokkal, hogy minden megállóhelyen van mosakodásra lehetőség. Ezután a következő megállónál nem száll le egyetlen egy matematikus sem a vonatról, hogy megmosakodjon. A rákövetkező megállón sem száll le egyetlen egy matematikus sem a vonatról, hogy megmosakodjon. Viszont a harmadik megállónál néhány matematikus leszáll a vonatról, hogy megmosakodjon.
Kérdés: Hány matematikus szállt le a vonatról mosakodás céljából?
|
|
| [2041] Lóczi Lajos | 2015-10-13 01:22:36 |
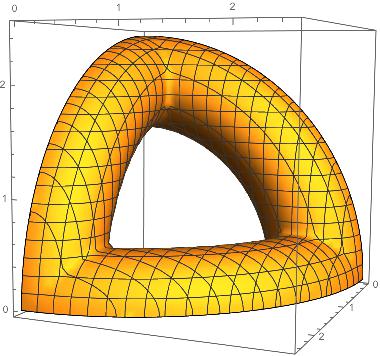
 A test térfogatának kérdését tekintve &tex;\displaystyle -&xet; az alábbiak a felszínre "még inkább" vonatkoznak &tex;\displaystyle -&xet; számomra úgy tűnik, hogy a térfogat nem fejezhető ki elemi függvényekkel. Még konkrét speciális esetben sem sikerült.
Tekintsük pl. az &tex;\displaystyle R=2&xet;, &tex;\displaystyle r=1/2&xet; esetet. Ekkor a test nyolcadrésze látható az ábrán. Különféle darabolásokkal a térfogat felírható kettős-, illetve egyszeres integrálokkal, ám úgy tűnik, hogy ezeknek nincs elemi primitív függvénye.
Természetesen numerikusan az integrálok, s így a térfogat is számolható.
Meg tudnánk például határozni az &tex;\displaystyle R=2&xet;, &tex;\displaystyle r=1/2&xet; esetben a teljes test közelítő térfogatát?
|
 |
| Előzmény: [2040] marcius8, 2015-10-07 08:22:45 |
|
| [2040] marcius8 | 2015-10-07 08:22:45 |
 Meg tudja nekem valaki mondani annak a testnek a térfogatát és felszínét, amely három, egymással egybevágó, egymásra merőleges, ugyanazzal a középponttal rendelkező tóruszból áll. Ismert a tóruszok középkörének "R" sugara és ismert a tóruszok kör alakú síkmetszetének "r" sugara, ahol r<R.
|
|
|
| [2038] Kemény Legény | 2015-09-23 12:17:44 |
 "- Van-e olyan négytagú (esetleg többtagú) számtani sorozat, amelynek minden tagja négyzetszám?"
Erre úgy tűnik, szintén tagadó a válasz: pl. Győri, Hajdu és Pintér cikke (Perfect powers from products of consecutive terms in arithmetic progression, Compositio Mathematica, 2009) alapján egy még erősebb állítás is igaz:
"We prove that for any positive integers x,d and k with gcd (x,d)=1 and 3<k<35, the product x(x+d)...(x+(k-1)d) cannot be a perfect power".
A cikk alapján úgy tűnik, az &tex;\displaystyle x(x+d)...(x+(k-1)d)=by^n, (x,d)=1&xet; egyenlet megoldását már Euler is vizsgálta a &tex;\displaystyle b=1, k=4, n=2&xet; esetre. Sőt Erdős sejtése az, hogy &tex;\displaystyle k>3&xet; esetén sosem lehet egy (rel. prímekből álló) számtani sorozat &tex;\displaystyle k&xet; egymást követő elemének szorzata teljes hatvány.
|
| Előzmény: [2035] marcius8, 2015-09-23 11:39:32 |
|
|









