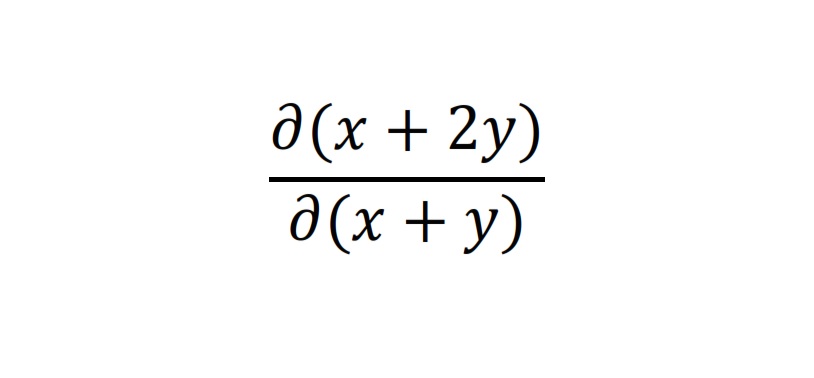| [2074] HoA | 2016-05-18 13:01:08 |
 Pontosítani kéne, mit jelent a szélességgel rendelkező mutató. Ha úgy érted, hogy mindegyik legalább d szélességű, a tengelynél is, akár lekerekítve,akkor az r = d/2 sugarú kis kör minden pontját mindig mindegyik mutató fedi. Vagy keskeny körcikk alakú mutatókra gondolsz, a tengelynél 0 szélességgel?
|
| Előzmény: [2072] Sinobi, 2016-04-10 22:30:58 |
|
| [2073] marcius8 | 2016-05-17 14:28:54 |
 Meg tudja valaki mondani, hogy egy normális (9x9-es) szudoku táblázatot hányféleképpen lehet kitölteni? Tisztelettel: Bertalan Zoltán.
|
|
| [2072] Sinobi | 2016-04-10 22:30:58 |
 n darab, szélességgel rendelkezö óramutató forog egy számlapon, vi e R sebességgel. Igaz-e, hogy ha volt legalább 1, akkor lesz végtelen sok idöintervallum, amikor az összes mutató 'összeér', fednek egy pontot?
|
|
| [2071] Jhony | 2016-03-27 13:36:35 |
 üdv. mindenkinek ! - a kérdésem ,,Prímek családfáját szerkeszteni,felállítani" - eszébe jutott e már valakinek is a Világon ? - vagyis ti erről mit tudtok,ugyanis mindezt mikor felvetettem az ,,openstudy.com/mathematics" angol nyelvű fórumon,azt kérdezték,mindez honnan jutott eszembe,hisz ezzel még nem állt elő - tudomásuk szerint - eddig senki sem az egész világon,vagyis első ember lennék,vagyok aki ezt a témát felveti,említi a matematika egész máig tartó történelme során - legalább is nem ismeretes ezzel kapcsolatban semmi - nos szerintetek,mi erről a véleményetek, tudomásotok, ismeretetek ? - ezzel kapcsolatban van egy vagyis szerkesztettem egy saját képlet által felállított prím-családfát,amit ott az oldalon megosztottam ideértve a szerkesztéshez,felállításhoz használt teljes útmutatót,leírást - ... - megosztva,feltéve kérdésemet,hogy mit vagyis hogyan ismertessem,közöljem a további prímekkel kapcsolatos úgy mond - szerintem - újdonságokat,sejtéseket,hipotéziseket ? - a válaszokat,hozzászólásokat előre is köszönöm szépen !
|
|
| [2070] 314 | 2016-02-28 17:01:54 |
 Üdv mindenkinek!
Azt szeretném kérdezni, hogy egy többváltozós függvényt hogyan kell deriválni egy szintén többváltozós függvény szerint? Pl. az ábrán látható kifejezést hogy lehet megoldani? Előre is köszönöm a választ!
|
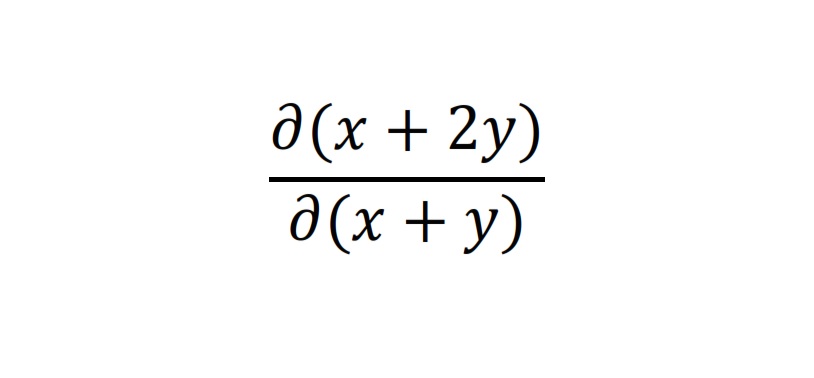 |
|
| [2069] epsilon | 2016-02-25 17:06:40 |
 Kedves lorantfy! Köszönöm a tippet! Valóban, a diákkori fizika órákon így állapítottuk meg a homogén lemezek (fém v műanyag, fa, stb)súlypontját, hogy két felfüggesztésnek vettük a metszéspontját, és meg is van a súlypont. (ha a súlypont a lemezen kívül esik, akkor már nehezebb dolgunk van). Ellenben az esetünkben több nehézségbe ütközünk: a felfüggesztést képzeletben kell elvégezni, és így a gravitáció irányát nem tudjuk PONTOSAN meghatározni, csak megközelítőleg elképzelni, és minden bizonnyal ha a leírt módszerrel a súlypontot meg is kapnánk, nem állíthatnánk teljes biztonsággal, hogy az az, mert ez csak egy fizikai mérés ami csak empirikusan megközelítő. De még tovább menve: a súlypont valamelyik rácspontra kell essen, és ha méréssel csak a közelébe esik, akkor nem tippelhetjük, hogy na ez a rácspont a leg közelebbi és kinevezzük súlypontnak. Összegezve: noha a felfüggesztési ötlet nem kizárt, de a matematikai pontosság szempontjából nem tartom valószínűnek, hogy a könyv szerzője erre a megoldásra gondolhatott, hiszen nem is aknáztuk ki lényegesen a rácspontokat amire a súlypont is esik. Várom tehát a további tippeket, hátha eltalálnánk, hogy mire gondolhatott a szerző a feladatok megoldásánál, amikor a súlypontot valamelyik rácspontra tervezte.
|
| Előzmény: [2068] lorantfy, 2016-02-23 21:23:23 |
|
| [2068] lorantfy | 2016-02-23 21:23:23 |
 Gondolatban fellógatod több kiválasztott szélső pontjánál fogva. Forgathatod a könyvet is. Behúzod a függőlegest, mikor úgy gondolod egyensúlyban lenne. 4-5 egyenest behúzva kiválasztod azt a hármat, ami egy kockában metszi egymást és kész. Az is az intelligenciához tartozik, hogy le tudsz játszani bizonyos dolgokat gondolatban!
|
| Előzmény: [2067] epsilon, 2016-02-23 13:22:03 |
|
| [2067] epsilon | 2016-02-23 13:22:03 |
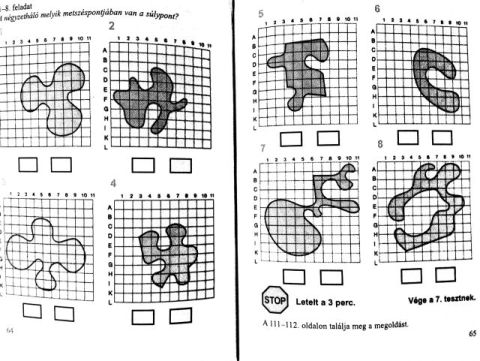
 Üdv Mindenkinek! Van egy régebbi IQ könyvem, J. E. Klausnitzer: IQ-Önteszt, Ciceró kiakó, 2005. Ebben van egy pár kérdés amelyekben rácspontokra rajzolt zárt görbevonal által határolt lapok súlypontjának a koordinátáit kell megmondani. Mindjárt jön a rajz is. Így saccolással általában eltalálható a súlypont koordinátája, de az lenne a kérdésem, hogy milyen szabály alapján kell meghatározni, hiszen nem is matematika könyvről van szó, hogy különféle elméleteket alkalmazzunk, hanem egyszerű IQ könyvről. Tudna-e valaki segíteni, hogy miként kell meghatározni a látható lapok súlypontjainak a koordinátáit? Ha szükség van az eredményre azt is küldöm, hiszen megvan, engem a "miért az a súlypont" kérdésre érdekelne a válasz! Előre is köszönöm!
|
 |
|
| [2066] Fálesz Mihály | 2015-12-30 09:42:03 |
 Arra gondoltam, hogy a Fejes-Tóth féle programot csináljuk végig.
Vegyük a poláris háromszöget. Az eredeti háromszög területéből következtethetünk a poláris háromszög kerületére. A poláris háromszögnek ismerjük egy csúcsát, az ebből kiinduló oldal-főköröket és a kerületet. Ezek meghatározzák a harmadik oldalhoz hozzáírt kört...
|
| Előzmény: [2064] Sinobi, 2015-12-28 23:20:22 |
|
| [2065] mooosa | 2015-12-29 17:15:00 |
 Legyen f eleme C(I) folytonos függvény az I = (0, 1) nyílt intervallumon, és tegyük fel, hogy lim x->0+ f(x) = +végtlen , határozzuk meg a g(x) := sin f(x) kompozíciófüggvény torlódási pontjainak halmazát x->+0-ra!
|
|
|
|
| [2062] Kemény Legény | 2015-12-15 13:50:00 |
 A dominált konvergencia tétellel/Fatou-lemmával valóban be lehet látni ilyeneket. Legyen az &tex;\displaystyle f_n&xet; függvény az &tex;\displaystyle n&xet;-edik halmaz (ami tetszőleges mérhető halmaz, így intervallum vagy akár intervallumok uniója is lehet) karakterisztikus függvénye (a halmazon 1, kívül 0). Ekkor a konstans 1 függvény egy integrálható majoránsa az &tex;\displaystyle f_n&xet;-eknek, így pl. a Fatou-lemma alapján &tex;\displaystyle limsup_{n\to\infty} \int f_n d\lambda\le \int limsup_{n\to\infty} f_n d\lambda&xet;, ahol az utóbbi limeszt pontonként értjük. Ha az &tex;\displaystyle f_n&xet;-eket meghatározó halmazok mértékére van egy közös alsó korlát K, akkor a bal oldali határérték is legalább K. Ha viszont egy pontot csak véges sok &tex;\displaystyle f_n&xet; fed le, akkor a jobb oldali integrálban szereplő &tex;\displaystyle limsup_{n\to\infty} f_n =0&xet; abban a pontban, egyébként 1. Mivel a jobb oldal nem lehet 0, így az az erősebb állítás is kijött, hogy a végtelen sokszor lefedett pontok halmaza nem lehet nullmértékű (sőt legalább K mértékű kell legyen).
|
| Előzmény: [2058] Sinobi, 2015-12-14 22:11:22 |
|
|
|
| [2059] Róbert Gida | 2015-12-14 23:42:42 |
 &tex;\displaystyle K>0&xet; alsó korláttal meg már igaz: legyen m>0 olyan egész, hogy &tex;\displaystyle \frac 1m<K&xet;, ekkor mivel minden intervallum legalább &tex;\displaystyle K&xet; hosszú, ezért tartalmaz legalább egy darab &tex;\displaystyle \frac lm&xet; alakú pontot. Így skatulyaelv miatt a végtelen sok intervallum valamelyik ilyen pontot végtelen sokszor tartalmazza. "Hasonló" gondolatmenet megy magasabb dimenzióban.
|
| Előzmény: [2058] Sinobi, 2015-12-14 22:11:22 |
|
| [2058] Sinobi | 2015-12-14 22:11:22 |
 És ha az intervallumok méretének adunk valami K alsó korlátot? (azt sejtem, hogy így már nem lehet)
És ha nagyobb (mondjuk 2) dimenzióban akarunk ilyen, >K méretű kockákkal fedni?
Vagy, ha még azt is megengedjük, hogy olyan alakzatokkal fedünk, amelyek előállnak véges sok téglatest uniójaként/metszeteként?
(ezeket próbáltam, sikertelenül. Állítólag valamelyik Lebesgue integrálos tétellel könnyű, de én azt nem tudom. Sőt, még az eredményt sem igazán.)
|
| Előzmény: [2056] Róbert Gida, 2015-12-14 17:34:37 |
|
|
|
| [2055] Sinobi | 2015-12-13 21:30:23 |
 Igaz-e hogy ha az egység intervallumba elhelyezünk végtelen sok zárt intervallumot, hogy az összhosszuk divergens, akkor biztosan létezni fog legalább 1 pont, amelyik végtelen sok által van lefedve? (R felett)
|
|
|
|
|
| [2051] emm | 2015-12-06 16:43:16 |
 &tex;\displaystyle D:=(A\cup B\cup C)^c&xet;, ekkor &tex;\displaystyle {P}(D)=1-p-q-r&xet;. Ekkor lényegében egy 4 oldalú cinkelt "kockával" dobunk. Legyen a keresett valószínűség &tex;\displaystyle R_n&xet;. Feltételezzünk arra, hogy az első dobás, amikor &tex;\displaystyle D&xet;-től különbözőt dobunk, &tex;\displaystyle k&xet;, legyen ez az esemény &tex;\displaystyle S_k&xet;, és a &tex;\displaystyle k&xet;-ik dobás &tex;\displaystyle X_k&xet;, a függetlenséget használva adódik, hogy:
&tex;\displaystyle
P(S_k)=P\left(X_{k}\neq D\cap\bigcap_{j=1}^{k-1}X_j=D \right)=P(X_k\neq D)\prod_{j=1}^{k-1}P(X_j=D)=(1-p-q-r)^{k-1}(p+q+r)
&xet;
Ebből a nekünk megfelelő eset az, amikor &tex;\displaystyle A&xet;-t dobunk, így az &tex;\displaystyle A&xet;, &tex;\displaystyle B&xet;, &tex;\displaystyle C&xet; események páronként kizáró volta miatt: miatt:
&tex;\displaystyle
P(S_k\cap X_k=A)=P\left(X_{k}=A\cap\bigcap_{j=1}^{k-1}X_j=D \right)=P(X_k=A)\prod_{j=1}^{k-1}P(X_j=D)(1-p-q-r)^{k-1}p
&xet;
Vagyis &tex;\displaystyle n&xet; dobás esetén, alkalmazva a mértani sor összegképletét:
&tex;\displaystyle
P(R_n)=\sum_{i=1}^nP(S_i\cap X_i=A)=p\sum_{i=0}^{n-1}(1-p-q-r)^{i}
=p\frac{1-(1-p-q-r)^n}{p+q+r}
&xet;
Ha &tex;\displaystyle p,q,r>0&xet;, akkor &tex;\displaystyle n\to\infty&xet; esetén a keresett valószínűség tart &tex;\displaystyle \frac{p}{p+q+r}&xet;-hez. (és nem okoz problémát, ha &tex;\displaystyle p+q+r=1&xet;).
|
| Előzmény: [2049] lorantfy, 2015-12-05 19:56:56 |
|
|